正交化原理与代码（施密特正交化与对称正交化）

学生而已

已于 2024-01-24 13:53:08 修改

阅读量1.1k

点赞数 10

文章标签：机器学习人工智能线性代数

于 2024-01-24 13:49:08 首次发布

本文链接：https://blog.csdn.net/vv0610_/article/details/135819325

版权

关键词：施密特正交化 (Gram-Schmidt Orthogonalization)，对称正交化/勒夫丁正交化（Symmetric Orthogonalization/ Per-Olov Löwdin Orthogonalization）

一、符号用语

在下文中，我们以加粗的大写字母来表示一个矩阵，如 “ $\textbf{\textit{W}}$ ”；以加粗斜体的小写字母辅以下标表示一个向量，如 “ $\textbf{\textit{w}}_i$ ”。另外，我们默认需要正交化的向量组为矩阵 $\textbf{\textit{W}}$ 的列。

$(\textbf{\textit{u}},\textbf{\textit{v}})$ 表示向量内积。

二、施密特正交化

施密特正交化其实很简单，套公式就行。

$proj_{\textbf{\textit{u}}}\textbf{\textit{v}}=\frac{(\textbf{\textit{u}},\textbf{\textit{v}})}{(\textbf{\textit{u}},\textbf{\textit{u}})}\textbf{\textit{u}} \\ \\ \textbf{\textit{u}}_k = \textbf{\textit{v}}_k-\sum_{j=1}^{k-1}proj_{\textbf{\textit{u}}_j}\textbf{\textit{v}}_k$

配合下图更好理解。

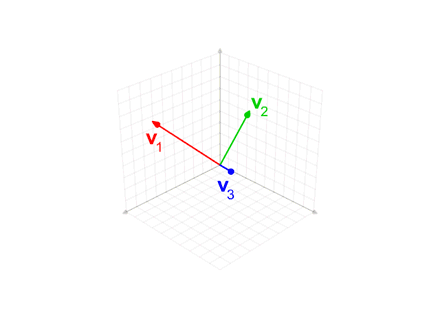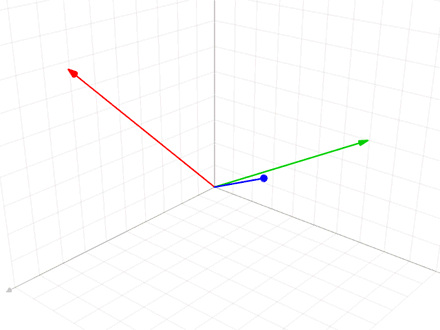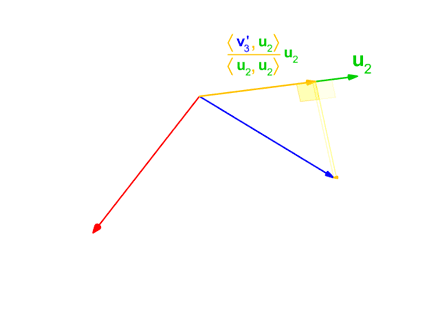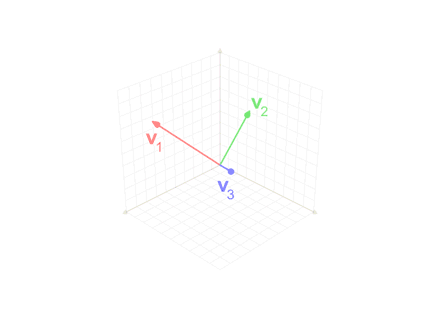
W[:, 0] = W[:, 0] / torch.norm(W[:, 0], 2) // 单位化
for v in range(W.size(1)):
    for u in range(v):
        W[:, v] = W[:, v] - proj(W[:, v], W[:, u])
    W[:, v] = W[:, v] / torch.norm(W[:, v], 2) // 单位化

//torch.norm(u) 就是向量u的二范数（模长）

def proj(v, u):
    coeff = torch.matmul(v, u) / torch.matmul(u, u) // 或者直接 v @ u
    return coeff * u

// torch.matmul(v, u) 表示矩阵乘法

这里就不再细说了，如果有问题可以留言。

三、对称正交化/勒夫丁正交化

这部分我在网上没有找到比较详细的资料，最早提出应该是在 Löwdin P O. On the nonorthogonality problem[M]//Advances in quantum chemistry. Academic Press, 1970, 5: 185-199. 但是很遗憾，这篇论文我没有找到原文，于是整合了我能找到的一些资料，以下部分翻译改编自书籍 Piela L. Ideas of quantum chemistry[M]. Elsevier, 2006. 的附录 J。

设想一组单位化的非正交基 $\textbf{\textit{w}}_i$ 组成的矩阵 $\textbf{\textit{W}}$ ，通过对 $\textbf{\textit{w}}_i$ 进行适当的线性组合，我们可以得到正交的 $\textbf{\textit{W}}$ （这里还是和施密特正交化的思想一致）。但是与施密特正交化不同，对称正交化均等地对待所有 $\textbf{\textit{w}}_i$ （插一句嘴，书中对这句话有部分解释：对于两个向量的施密特正交化过程来说，我们总是从一个向量上减去另一个向量投影的一定倍数，就此而言两个向量并没有被同等对待。再换句话说，和特征值有关，建议大伙用到再深究）。

公式如下： $\textbf{\textit{W}}\leftarrow(\textbf{\textit{W}}\textbf{\textit{W}}^T)^{-\frac{1}{2}}\textbf{\textit{W}}$

如果我们进行验证不难发现， $((\textbf{\textit{W}}\textbf{\textit{W}}^T)^{-\frac{1}{2}}\textbf{\textit{W}})^T((\textbf{\textit{W}}\textbf{\textit{W}}^T)^{-\frac{1}{2}}\textbf{\textit{W}})=I$

接着是 -1/2 次幂的计算过程，先展示书上给出的过程：

1. 对 $\textbf{\textit{W}}\textbf{\textit{W}}^T$ 做特征分解，使得 $\textbf{\textit{L}} = \textbf{\textit{U}}^T\textbf{\textit{W}}\textbf{\textit{W}}^T\textbf{\textit{U}}$ ，此时的 $\textbf{\textit{L}}$ 是包含全部特征值的对角矩阵

2. 计算 $\textbf{\textit{L}}^{\frac{1}{2}}$ ，显然 $\textbf{\textit{L}}^{-\frac{1}{2}}=(\textbf{\textit{L}}^{\frac{1}{2}})^{-1}$

3. 根据相似理论， $(\textbf{\textit{W}}\textbf{\textit{W}}^T)^{-\frac{1}{2}}=\textbf{\textit{U}}\textbf{\textit{L}}^{-\frac{1}{2}}\textbf{\textit{U}}^T$

实操的时候 torch.eig 会产生复数，开根号可能会出问题，所以这里介绍一种更简便的方法：

1. 对 $\textbf{\textit{W}}$ 做奇异值分解，使得 $\textbf{\textit{W}} = \textbf{\textit{U}}\textbf{\textit{S}}\textbf{\textit{V}}^T$ ，此时的 $\textbf{\textit{S}}$ 是包含全部奇异值的对角矩阵。显然，这里的 $\textbf{\textit{U}}$ 和前面的 $\textbf{\textit{U}}$ 一模一样（误差除外），且 $\textbf{\textit{S}}=\textbf{\textit{L}}^{\frac{1}{2}}$

2. 于是 $(\textbf{\textit{W}}\textbf{\textit{W}}^T)^{-\frac{1}{2}}=\textbf{\textit{U}}\textbf{\textit{S}}^{-1}\textbf{\textit{U}}^T$

def symmetric_orthogonalization(W):
    W = W.float()
    U, S, _ = torch.linalg.svd(W)
    r = torch.matrix_rank(W)
    S = torch.inverse(torch.diag(S))
    U = U[:, 0:r]
    res = U @ S @ U.t() @ W
    return res

实际运用中，在速度上，奇异值分解>>特征值分解>施密特正交化。

最后给出一个测试用例：

import torch

def symmetric_orthogonalization(W):
    W = W.float()
    U, S, _ = torch.linalg.svd(W)
    r = torch.matrix_rank(W)
    S = torch.inverse(torch.diag(S))
    U = U[:, 0:r]
    res = U @ S @ U.t() @ W
    return res

W = torch.tensor([
    [1, 2],
    [3, 4],
    [5, 6]
])

W = symmetric_orthogonalization(W)

print(W.t()@W)

学生而已

关注

10
点赞
踩
8

收藏

觉得还不错? 一键收藏
2
评论
正交化原理与代码（施密特正交化与对称正交化）

关键词：施密特正交化 (Gram-Schmidt Orthogonalization)，对称正交化/勒夫丁正交化（Symmetric Orthogonalization/ Per-Olov Löwdin Orthogonalization）
复制链接

扫一扫