在基于特征点法的视觉SLAM中,当一个地图点在多张图像中获取到多个观测中,利用三角化原理进行深度初值的计算,接着利用BA(bundle adjustment)对深度进行优化。然而在DSO中,作者采用的是深度滤波器的思想,深度滤波器是单目直接法种一个非常重要的环节。DSO中的深度估计思想也是完全来源于作者的另一篇文章(Semi-Dense Visual Odometry for a Monocular Camera),对这篇文章有一定了解后才能比较容易看懂关于深度估计的源码,有兴趣可以去看看。
首先,单目的深度估计使用了类似于立体视觉的深度计算方法,所不同的是在立体视觉中,基线是已知且固定的。但是对于单目深度估计来说,一般都是利用时序的前后帧图像进行深度恢复,因此基线是变化不定的。如下图所示,基线较小的时候估计的深度精度较低(这里可以简要理解为图像上一个像素的误差会引起深度的变化较大,下文会具体分析如何根据像素不确定度确定深度不确定度),然而在基线较大时,存在较多错误的误匹配点,造成深度的估计完全不准确。按照笔者自己的理解,应该是当基线很小时,关键帧的特征点在当前帧中的极线搜索长度比较小,因此根据灰度块匹配可以较准确的找到匹配点,但是由于基线较小,在三角化恢复深度时,图像上一个像素的不确定度会造成较大的深度不确定度,此时准确度可以,精度不行;当基线很大时,关键帧的特征点在当前帧中的对应极线搜索长度较大,由于图像像素梯度的强非凸性,造成灰度块匹配时存在多个局部最佳匹配点,如果陷入局部最优匹配点,那么三角恢复的深度就完全错误了,如果正确找到了,那么这时候由于基线较大,所以深度恢复会比较准确,此时精度很高,但是准确度可能会降低。所以作者提出在小基线和大基线之间存在精度和准确度的权衡。这一块的理解不确定完全正确,如有不对之处,还望指正,谢谢。
经过博友Operaboss的提醒,发现自己当初在这个地方的理解出现了错误;其实应该是当基线很小时,前后两帧图像的变化不大,基于ncc的图像块匹配算法能够较精确的找到最优值,然而由于基线较短,在三角化深度恢复的时,图像上一个像素的不确定度会造成较大的深度不确定度,此时匹配准确度较高,然后深度估计精度不够;当基线较大时,前后两帧图像的变化较大,在极线上搜索时,基于ncc图像块匹配的能量函数呈现较强的非凸性,存在多个局部最优值,因此特征点的匹配很容易出现错误,造成准确度下降,但如果匹配结果较为理想,那么基于大基线,三角恢复的深度将更加准确,可以理解为准确度降低,然后精度较高。

那么DSO作者是如何解决这个问题的呢? 首先应该清楚在进行深度估计时,总是利用新来的非关键帧去更新关键帧的深度和不确定度。如下图所示,假设我们需要估计最近关键帧中特征点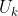 对应的深度和深度不确定度,那么该怎么进行呢?
对应的深度和深度不确定度,那么该怎么进行呢?
- 首先作者先给特征点
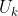 赋予一个非常大的深度不确定度,假设是0-100(单位m),这显然是合理的。
赋予一个非常大的深度不确定度,假设是0-100(单位m),这显然是合理的。 - 接着当帧A到来时,利用Tracking流程成功的估计了最近关键帧到A帧的位姿变化,显然这个时候,最近关键帧与A帧组成的立体几何双目基线一般是比较小的,这个时候通过灰度块匹配能够大致确定
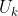 特征点在A帧对应的匹配像素位置
特征点在A帧对应的匹配像素位置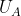 ,并给出匹配不确定度(如何计算匹配的不确定度会在下文中具体介绍)。一旦有了前后两帧的匹配点对和匹配点对的不确定度,结合两帧的位姿关系就可以恢复出大致的深度范围,但这个时候由于基线较小,估计的深度精度不够,深度不确定度会比较大,但是至少在正确的范围内。
,并给出匹配不确定度(如何计算匹配的不确定度会在下文中具体介绍)。一旦有了前后两帧的匹配点对和匹配点对的不确定度,结合两帧的位姿关系就可以恢复出大致的深度范围,但这个时候由于基线较小,估计的深度精度不够,深度不确定度会比较大,但是至少在正确的范围内。 - 我们已经利用帧A的信息缩小了深度不确定度,随着后续帧B的到来,利用同样的方式,在B帧上确定与特征点
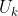 匹配的特征点
匹配的特征点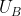 和匹配不确定度,这个时候由于我们已经利用了小基线确定了深度的大致范围,因此在大基线的时候,就不会出现较长的极限搜索范围,这个时候就能很好的弥补大基线存在很多局部最优匹配点的问题。又由于最近关键帧与B帧的基线距离逐渐增加,因此对深度的估计也会越来越准确。
和匹配不确定度,这个时候由于我们已经利用了小基线确定了深度的大致范围,因此在大基线的时候,就不会出现较长的极限搜索范围,这个时候就能很好的弥补大基线存在很多局部最优匹配点的问题。又由于最近关键帧与B帧的基线距离逐渐增加,因此对深度的估计也会越来越准确。 - 重复以上的深度估计过程直到深度估计不确定度在一个较小的范围内,我们认为深度点成熟,可以加入地图进行后端优化了。

经过上面流程的梳理,自然就会有以下几个问题需要解决:
- 如何确定匹配点位置
- 如何确定匹配点的像素不确定度
- 如何根据匹配点的不确定度计算相应的深度不确定度,即深度更新
为了解决上述三个问题,需要一系列的公式推导,首先进行一些必要的参数符号说明。假设特征点在最近关键帧上图像上的像素表示为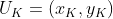 ,在归一化平面的坐标表示为
,在归一化平面的坐标表示为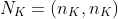 , 该特征点在最近关键帧坐标系下的逆深度表示为
, 该特征点在最近关键帧坐标系下的逆深度表示为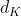 ,其对应的逆深度不确定度为
,其对应的逆深度不确定度为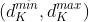 ;同样的方式该特征点在帧A图像上的像素表示为
;同样的方式该特征点在帧A图像上的像素表示为 ,在归一化平面的坐标表示为
,在归一化平面的坐标表示为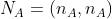 , 该特征点在帧A坐标系下的逆深度表示为
, 该特征点在帧A坐标系下的逆深度表示为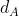 ,其对应的逆深度不确定度为
,其对应的逆深度不确定度为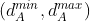 。从最近关键帧到帧A的旋转矩阵表示为
。从最近关键帧到帧A的旋转矩阵表示为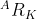 ,平移部分表示为
,平移部分表示为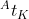 ;假设相机内参矩阵为
;假设相机内参矩阵为 。
。
像素点匹配
先假设我们需要获取关键帧上特征点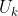 在帧A图像上的匹配点位置,那么根据其逆深度的不确定度
在帧A图像上的匹配点位置,那么根据其逆深度的不确定度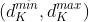 ,基于位姿变换和投影关系可以分别求得其帧A上对应的极线搜索范围。对于逆深度
,基于位姿变换和投影关系可以分别求得其帧A上对应的极线搜索范围。对于逆深度 ,假设在帧A上的投影坐标为
,假设在帧A上的投影坐标为 ,对于逆深度
,对于逆深度 ,假设在帧A上的投影坐标为
,假设在帧A上的投影坐标为 。
。


那么图像上以 和
和 为端点的直线段就是需要搜索的极线区间,在这个区域内去确定特征点
为端点的直线段就是需要搜索的极线区间,在这个区域内去确定特征点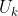 的匹配点
的匹配点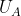 。这一步从源码实现来看还是存在很多技巧的,在代码解析处h会详细介绍。常见的灰度图像匹配算法包括平均绝对差算法(MAD)、绝对误差和算法(SAD)、误差平方和算法(SSD)、平均误差平方和算法(MSD)、归一化积相关算法(NCC)等等,如果需要进一步了解可以移步网址。在DSO中,作者采用SSD算法,用公式表示为:
。这一步从源码实现来看还是存在很多技巧的,在代码解析处h会详细介绍。常见的灰度图像匹配算法包括平均绝对差算法(MAD)、绝对误差和算法(SAD)、误差平方和算法(SSD)、平均误差平方和算法(MSD)、归一化积相关算法(NCC)等等,如果需要进一步了解可以移步网址。在DSO中,作者采用SSD算法,用公式表示为:
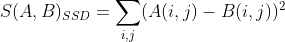
SSD计算的窗口使周围特定的8个位置,如下图所示。采用8个位置是根据作者多次试验得到的速度和精度上的一个综合考虑(SSD计算邻域位置,8个点也是为了SSE加速考虑)

匹配点像素不确定度的计算
在LSD中,作者提出观点匹配点像素的不确定度来自两个方向,一部分是由于相机位姿和内参的误差引起极线计算中的几何误差;第二部分是由于图像成像过程中的光度误差。由于在DSO中,作者已经提前对成像过程进行建模或者实时的优化光度参数,所以将不再考虑图形成像过程中带来的误差,唯一的匹配点像素不确定度将全部来自与几何误差。接下来的不确定度的推导全部来自于作者的论文"Semi-Dense Visual Odometry for a Monocular Camera"。
当我们把一个3D点从关键帧投影到参考帧进行极线搜索匹配的时候,理想状态下,投影点就是匹配点。但是因为估计深度在一个范围内,所以只能在极线上进行搜索寻找最佳匹配点。但是又由于相机位姿和内参不是完全准确的,因此极线存在偏移误差,那么在极线上搜索出的匹配点与真实投影点也就存在相应的误差,这部分误差就是几何误差的具体来源。
为了数学模型的建立,作者将这种极线的误差偏移简化为方向不变而改变位置。首先极线的表达式定位为:
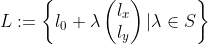
其中 为特征点在深度为无穷大时对应的在参考帧的投影点,表示了极线的初始位置,
为特征点在深度为无穷大时对应的在参考帧的投影点,表示了极线的初始位置,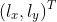 为单位极线方向,
为单位极线方向, 表示在极线上的视差disparity,
表示在极线上的视差disparity,  为在极线上搜索的范围。几何误差便是指
为在极线上搜索的范围。几何误差便是指 的误差偏移。如下图所示,点A为理想点(过A点的实线为理想极线),B为投影点(过B点的实线为实际极线),我们在实际极线上进行搜索匹配。在这里假设了局部光度变化是线性的,图中虚线是等光度线,因此我们搜索到过A的等光度线上的点C。点AB之间的偏差表示了极线位置误差,点BC之间偏差表示由此引起的几何误差。同时可以看出,极线与等光度线的夹角越小,产生的几何误差越大。按照论文中的表示,用
的误差偏移。如下图所示,点A为理想点(过A点的实线为理想极线),B为投影点(过B点的实线为实际极线),我们在实际极线上进行搜索匹配。在这里假设了局部光度变化是线性的,图中虚线是等光度线,因此我们搜索到过A的等光度线上的点C。点AB之间的偏差表示了极线位置误差,点BC之间偏差表示由此引起的几何误差。同时可以看出,极线与等光度线的夹角越小,产生的几何误差越大。按照论文中的表示,用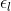 表示极线初始位置误差,用
表示极线初始位置误差,用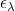 表示由此引起的在极线上的匹配误差。
表示由此引起的在极线上的匹配误差。
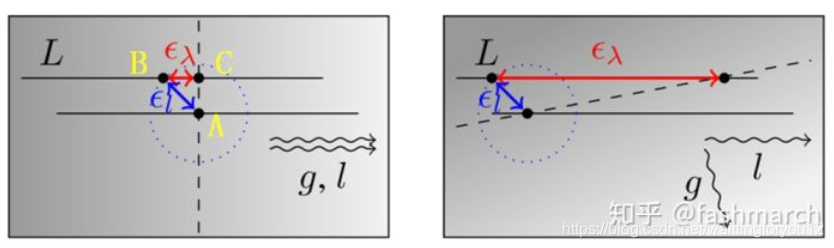
图:极线方向与梯度方向的夹角与几何误差的关系
(图片来自知乎https://zhuanlan.zhihu.com/p/47742232)
上述的表述可以直观的这么去理解,我们试图在极线上搜索特征点在当前帧的匹配点,特征点匹配算法一般是基于图像块的灰度值。如果极线的方向和图像像素的梯度方向是垂直的,那么可以大致认为沿着极线方向,像素没有发生太多的变化,基于图像块的匹配算法会很难寻找出最优的匹配点。然而如果极线的方向与图像像素梯度方向是平行的,那么沿着极线方向,图像像素值变化较大,这个时候才用图像块的匹配算法可以很明显的找到那个最优的匹配点。
在极线搜索时,我们希望找到满足以下方程的点:

上式中,方程左边是极线方程,方程右边是等光度线方程,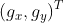 为图像梯度,与等光度线垂直。
为图像梯度,与等光度线垂直。 就是我们要求取的值,它表示在极限上搜索的长度,在论文中表述为视差disparity,极线上该位置就是需要寻找的匹配点。
就是我们要求取的值,它表示在极限上搜索的长度,在论文中表述为视差disparity,极线上该位置就是需要寻找的匹配点。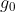 就是在关键帧上特征点的像素值。将上式展开:
就是在关键帧上特征点的像素值。将上式展开:
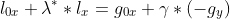
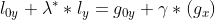
消去参数 便可以得到:
便可以得到:

这个时候就成功建立了极线初始位置 与我们需要获取的匹配点视差
与我们需要获取的匹配点视差 的关系。
的关系。
此时假设极线初始位置受到噪声影响,在图像x,y方向的方差均假设为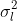 ,那么根据上式关系可以顺利推导出由此引起的极线上的匹配不确定度:
,那么根据上式关系可以顺利推导出由此引起的极线上的匹配不确定度:
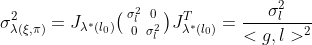
深度估计以及不确定度计算
根据上述两小节的内容,已经可以成功的找到图像匹配对以及匹配的不确定度,那么接下来自然而然的便是通过图像匹配对计算深度,以及根据极线上的像素匹配不确定度计算深度不确定度。
首先推导深度的计算,推导完全基于DSO中代码表示进行的。假设相机内参矩阵为 ,关键帧图像上特征点的齐次像素坐标为
,关键帧图像上特征点的齐次像素坐标为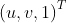 ,从关键帧到当前帧的旋转矩阵为
,从关键帧到当前帧的旋转矩阵为 , 平移向量为
, 平移向量为 ,根据极限搜索确定在当前帧的匹配像素点其次坐标为
,根据极限搜索确定在当前帧的匹配像素点其次坐标为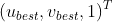 ,假设特征点在关键帧中的逆深度为
,假设特征点在关键帧中的逆深度为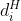 ,在当前帧的逆深度表示为
,在当前帧的逆深度表示为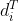 (H上标代指Host, 在论文和源码中作者一般用Host frame表示特征点首次出现的帧, T上标代码Target, 作者用target frame代指特征点形成投影的帧)。那么根据坐标转换可以建立如下的等式:
(H上标代指Host, 在论文和源码中作者一般用Host frame表示特征点首次出现的帧, T上标代码Target, 作者用target frame代指特征点形成投影的帧)。那么根据坐标转换可以建立如下的等式:

整理上式可得:
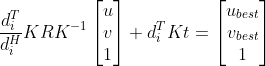
现在按照源码的表述假设:
接着将矩阵两边展开,可以获得是三个方程:
![\frac{d_{i}^{T}}{d_{i}^{H}}*pr[0] + d_{i}^{T}*hosttoFrame\_kt[0] = u_{best}](https://i-blog.csdnimg.cn/blog_migrate/eff1f65b68f4944ce98147e61af71b4b.gif)
![\frac{d_{i}^{T}}{d_{i}^{H}}*pr[1] + d_{i}^{T}*hosttoFrame\_kt[1] = v_{best}](https://i-blog.csdnimg.cn/blog_migrate/687a02df84e4fe8285e0b6ef28f5175b.gif)
![\frac{d_{i}^{T}}{d_{i}^{H}}*pr[2] + d_{i}^{T}*hosttoFrame\_kt[2] = 1](https://i-blog.csdnimg.cn/blog_migrate/8c961d8a3271ddd7ffad8f6be1af18c1.gif)
三个方程,两个未知数,可以利用1式和3式求解逆深度,也可以利用2式和3式1求解逆深度,假设利用1式和3式,最终求得逆深度表述为:
![d_i^{H} = \frac{pr[0] - u_{best}*pr[2]}{u_{best}*hostToFrame\_kt[2] - hostToFrame\_kt[0]}](https://i-blog.csdnimg.cn/blog_migrate/1a6614c7874de56ee2ab7783434a4d0e.gif)
有了以上求解逆深度的公式,那么根据匹配点的不确定度,也可以非常容易的求解逆深度的不确定度了。假设匹配点的不确定度已经获取为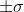 ,那么此时匹配点就分别表示为
,那么此时匹配点就分别表示为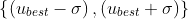 。根据上式可以就可以方便的求解深度不确定度为:
。根据上式可以就可以方便的求解深度不确定度为:
![d_{imin}^{H} = \frac{pr[0] - (u_{best} - \sigma )*pr[2]}{(u_{best} - \sigma )*hostToFrame\_kt[2] - hostToFrame\_kt[0]}](https://i-blog.csdnimg.cn/blog_migrate/504bcb3096d0067229a54b88943bf57a.gif)
![d_{imin}^{H} = \frac{pr[0] - (u_{best} + \sigma )*pr[2]}{(u_{best} + \sigma )*hostToFrame\_kt[2] - hostToFrame\_kt[0]}](https://i-blog.csdnimg.cn/blog_migrate/e59a277e6299b37f35389a354dfd0fa0.gif)
至此,DSO深度滤波的理论推导已经全部完成,接下来结合代码进行分析。
代码解读
DSO中深度滤波的代码主要是src/FullSystem/ImmaturePoint.h 和 src/FullSystem/ImmaturePoint.cpp文件,首先从头文件开始。作者定义了ImmaturePoint这个类用来表示未成熟的地图点,只有通过不断的深度滤波,未成熟地图点的深度收敛后才加入后端进行优化。这个类的定义如下所示,针对每个成员函数都有相应的解释。
class ImmaturePoint
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
// 存储的特征点周围8邻域点的像素值
float color[MAX_RES_PER_POINT];
// 存储的是周围8邻域像素梯度值
float weights[MAX_RES_PER_POINT];
// 计算8邻域梯度Hessian矩阵 sum{(dx, dy)^T * (dx, dy)}
// 上述三个变量都是在构造函数的时候进行计算, 方便后续使用
Mat22f gradH;
Vec2f gradH_ev;
Mat22f gradH_eig;
float energyTH;
// 特征点的像素坐标
float u,v;
// 指针指向特征点的主导帧
FrameHessian* host;
int idxInImmaturePoints;
// 特征点质量
float quality;
// 选取的类型
float my_type;
// 深度滤波中估计的最小逆深度值
float idepth_min;
// 深度滤波中估计的最大逆深度值
float idepth_max;
// 构造函数
ImmaturePoint(int u_, int v_, FrameHessian* host_, float type, CalibHessian* Hcalib);
~ImmaturePoint();
// 这个函数是深度滤波的核心,调用此函数可以不断的更新特征点的深度直至深度收敛
ImmaturePointStatus traceOn(FrameHessian* frame, const Mat33f &hostToFrame_KRKi,
const Vec3f &hostToFrame_kt, const Vec2f &hostToFrame_affine,
CalibHessian* Hcalib, bool debugPrint=false);
// 记录上一次深度滤波的状态
ImmaturePointStatus lastTraceStatus;
// 记录上一次最佳匹配点的位置
Vec2f lastTraceUV;
// 记录上一次的视差
float lastTracePixelInterval;
float idepth_GT;
// 这个函数用于逆深度高斯牛顿优化
double linearizeResidual(
CalibHessian* Hcalib, const float outlierTHSlack,
ImmaturePointTemporaryResidual* tmpRes,
float &Hdd, float &bd,
float idepth);
// 未用到
float getdPixdd(
CalibHessian* Hcalib,
ImmaturePointTemporaryResidual* tmpRes,
float idepth);
// 为用到
float calcResidual(
CalibHessian * HCalib, const float outlierTHSlack,
ImmaturePointTemporaryResidual* tmpRes,
float idepth);
};接下来主要解析核心深度滤波函数,这个函数在实现上有很多技巧,值得学习。
ImmaturePointStatus traceOn(FrameHessian* frame, const Mat33f &hostToFrame_KRKi,
const Vec3f &hostToFrame_kt, const Vec2f &hostToFrame_affine,
CalibHessian* Hcalib, bool debugPrint=false);首先需要说明的是,作者利用枚举表示了不同的深度跟新状态,简要进行说明。
- IPS_GOOD 表示最近一次在极线上进行特征点的匹配时成功的。
- IPS_OOB 表示跟踪结束,或者追踪的特征点在当前帧的投用已经出了图像边界。
- IPS_OUTLIER 表示跟踪失败,即没有在极线上搜索到匹配点。
- IPS_SKIPPED 表示虽然成功跟踪,但是匹配点对之间的视差非常小,可以跳过,因为视差非常小不利于深度计算和更新。
- IPS_BADCONDITION 表示其他一些糟糕的情况导致匹配跟踪失败。
- IPS_UNINITIALIZED 表示还没有进行过深度更新
enum ImmaturePointStatus
{
IPS_GOOD=0, // traced well and good
IPS_OOB, // OOB: end tracking & marginalize!
IPS_OUTLIER, // energy too high: if happens again: outlier!
IPS_SKIPPED, // traced well and good (but not actually traced).
IPS_BADCONDITION, // not traced because of bad condition.
IPS_UNINITIALIZED // not even traced once.
};进入函数首先进行判断,上一次跟踪是否出了图像边界,如果出了图像边界,那么直接返回这个状态,不需要再进行后续操作了。然后就是设定最长的基线搜索长度,作者设定的阈值为0.027,至于为什么定这个值,还不清楚。
if(lastTraceStatus == ImmaturePointStatus::IPS_OOB) return lastTraceStatus;
debugPrint = false;
float maxPixSearch = (wG[0]+hG[0])*setting_maxPixSearch;根据最小逆深度投影到traced frame中,获取像素值,如果像素值超过图像边界,返回状态IPS_OOB。
Vec3f pr = hostToFrame_KRKi * Vec3f(u, v, 1);
Vec3f ptpMin = pr + hostToFrame_kt * idepth_min;
float uMin = ptpMin[0]/ptpMin[2];
float vMin = ptpMin[1]/ptpMin[2];
if(!(uMin > 4 && vMin > 4 && uMin < wG[0]-5 && vMin < hG[0]-5))
{
if(debugPrint)
printf("OOB uMin %f %f - %f %f %f (id %f-%f)!\n",
u, v, uMin, vMin, ptpMin[2], idepth_min, idepth_max);
lastTraceUV = Vec2f(-1, -1);
lastTracePixelInterval = 0;
return lastTraceStatus = ImmaturePointStatus::IPS_OOB;
}
float dist;
float uMax;
float vMax;
Vec3f ptpMax;接着就是处理最大逆深度的投影,作者在初始化的时候假设最大逆深度为Nan,所以在第一次更新的时候,代码首先会进入else分支,在else分支,假设了最大深度为100,其逆深度自然是0.01,获取到了此时的投影位置,根据前面获得的最小逆深度的投影位置,就可以求取极线的方向。前面固定了最大的极线搜索长度为maxPixSearch,因此根据最小逆深度投影位置,极线方向和极线最大搜索长度就可以唯一确定最大逆深度的投影点。如果最大逆深度投影点超出图像边界,同样返回状态IPS_OOB;
如果不是第一次更新,那么就是常规的根据最大逆深度获取投影点,判断是否出界;接着计算最小逆深度投影点和最大逆深度投影点之间的像素距离,如果没有超过2个像素大小,表示足够准确,没必要进行更新操作,返回状态IPS_SKIPPED;
if (std::isfinite(idepth_max)) //进入这个条件已经不是第一次更新了
{
ptpMax = pr + hostToFrame_kt * idepth_max;
uMax = ptpMax[0] / ptpMax[2];
vMax = ptpMax[1] / ptpMax[2];
if (!(uMax > 4 && vMax > 4 && uMax < wG[0] - 5 && vMax < hG[0] - 5))
{
if (debugPrint)
printf("OOB uMax %f %f - %f %f!\n", u, v, uMax, vMax);
lastTraceUV = Vec2f(-1, -1);
lastTracePixelInterval = 0;
return lastTraceStatus = ImmaturePointStatus::IPS_OOB;
}
//====check their distance, everything is below 2px is ok(to skip)
dist = (uMin - uMax) * (uMin - uMax) + (vMin - vMax) * (vMin - vMax);
dist = sqrtf(dist);
if (dist < setting_trace_slackInterval)
{
if (debugPrint)
printf("TOO CERTAIN ALREADY(dist %f)!\n", dist);
lastTraceUV = Vec2f(uMax + uMin, vMax + vMin) * 0.5;
lastTracePixelInterval = dist;
return lastTraceStatus = ImmaturePointStatus::IPS_SKIPPED;
}
assert(dist > 0);
}
else //如果是第一次更新,那么最大搜索长度固定为maxPixSearch
{
dist = maxPixSearch;
// project to arbitrary depth to get direction
// 任意投影到较为合理的最大逆深度,深度100,只为获得极线方向
ptpMax = pr + hostToFrame_kt * 0.01;
uMax = ptpMax[0] / ptpMax[2];
vMax = ptpMax[1] / ptpMax[2];
//direction
float dx = uMax - uMin;
float dy = vMax - vMin;
float d = 1.0f / sqrtf(dx * dx + dy * dy);
uMax = uMin + dist * dx * d;
vMax = vMin + dist * dy * d;
//may still be out
if (!(uMax > 4 && vMax > 4 && uMax < wG[0] - 5 && vMax < hG[0] - 5))
{
if (debugPrint) printf("OOB uMax-coarse %f %f %f!\n", uMax, vMax, ptpMax[2]);
lastTraceUV = Vec2f(-1, -1);
lastTracePixelInterval = 0;
return lastTraceStatus = ImmaturePointStatus::IPS_OOB;
}
assert(dist > 0);
}接下里的代码是计算像素匹配不确定度, Vec2f(dx, dy)表示极线方向,Vec2f(dy, -dx)表示极线的垂直方向,gradH表示的是特征点周围8邻域像素hessian梯度求和。按照前面理论分析,当极线的方向和特征点梯度的方向垂直时,匹配误差较大,当极线方向和特征点梯度平行时,匹配误差最小;因此代码中的a可以表示极线与梯度的点乘再求平方,即前面公式中的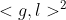 . 假设极线与梯度平行,此时a特别大,b相对较小,因此(a+b)/a接近于1,那么在最优的情况下每一个像素会产生0.4个像素的误差;此时的0.4可以看做基础噪声
. 假设极线与梯度平行,此时a特别大,b相对较小,因此(a+b)/a接近于1,那么在最优的情况下每一个像素会产生0.4个像素的误差;此时的0.4可以看做基础噪声 ; 如果极线和梯度垂直,此时a非常小,而b非常大,所以误差就会明显增加;此处笔者只是大致的进行分析,至于公式为什么为这么给出也是不太清楚, 还请大家指正。
; 如果极线和梯度垂直,此时a非常小,而b非常大,所以误差就会明显增加;此处笔者只是大致的进行分析,至于公式为什么为这么给出也是不太清楚, 还请大家指正。
// =======compute error-bounds on result in pixel. if new interval is not at least 1/2 of the old, SKIP
float dx = setting_trace_stepsize * (uMax - uMin);
float dy = setting_trace_stepsize * (vMax - vMin);
float a = (Vec2f(dx, dy).transpose() * gradH * Vec2f(dx, dy));
float b = (Vec2f(dy, -dx).transpose() * gradH * Vec2f(dy, -dx));
float errorInPixel = 0.2f + 0.2f * (a + b) / a;
if (errorInPixel * setting_trace_minImprovementFactor > dist && std::isfinite(idepth_max))
{
if (debugPrint)
printf("NO SIGNIFICANT IMPROVEMNET (%f)!\n", errorInPixel);
lastTraceUV = Vec2f(uMax + uMin, vMax + vMin) * 0.5f;
lastTracePixelInterval = dist;
return lastTraceStatus = ImmaturePointStatus::IPS_BADCONDITION;
}
if (errorInPixel > 10) errorInPixel = 10;完成上述的处理后就是具体的在极线上搜索匹配点的工作,在极线上以1个像素为步长进行搜索。每到一个像素位置计算其8邻域图像块的灰度残差,并将最小残差和最小残差对应的像素位置进行记录。最多进行100个步长的搜索。
int numSteps = 1.9999f + dist / setting_trace_stepsize;
Mat22f Rplane = hostToFrame_KRKi.topLeftCorner<2, 2>();
float randShift = uMin * 1000 - floorf(uMin * 1000);
float ptx = uMin - randShift * dx;
float pty = vMin - randShift * dy;
Vec2f rotatePattern[MAX_RES_PER_POINT];
for (int idx = 0; idx < patternNum; idx++)
{
rotatePattern[idx] = Rplane * Vec2f(patternP[idx][0], patternP[idx][1]);
}
if (!std::isfinite(dx) || !std::isfinite(dy))
{
lastTracePixelInterval = 0;
lastTraceUV = Vec2f(-1, -1);
return lastTraceStatus = ImmaturePointStatus::IPS_OOB;
}
float errors[100];
float bestU = 0, bestV = 0, bestEnergy = 1e10;
int bestIdx = -1;
if (numSteps >= 100) numSteps = 99;
for (int i = 0; i < numSteps; i++)
{
float energy = 0;
for (int idx = 0; idx < patternNum; idx++)
{
float hitcolor = getInterpolatedElement31(
frame->dI,
(float)(ptx + rotatePattern[idx][0]),
(float)(pty + rotatePattern[idx][1]),
wG[0]);
if (!std::isfinite(hitcolor)) {energy += 1e5; continue;}
float residual = hitcolor - (float)(hostToFrame_affine[0] * color[idx] + hostToFrame_affine[1]);
float hw = fabs(residual) < setting_huberTH ? 1 : setting_huberTH / fabs(residual);
energy += hw * residual * residual * (2 - hw);
}
if (debugPrint)
printf("step %.1f %.1f (id %f): energy = %f!\n", ptx, pty, 0.0f, energy);
errors[i] = energy;
if (energy < bestEnergy)
{
bestU = ptx;
bestV = pty;
bestEnergy = energy;
bestIdx = i;
}
ptx += dx;
pty += dy;
}根据上面一步,已经找到了1个像素精度的最佳匹配点,接着利用高斯牛顿算法继续优化亚像素级别的最佳匹配位置。里面无非就是计算残差以及计算残差对像素位置的雅克比,就不再赘述。
//============do GN optimization======================================
float uBak = bestU, vBak = bestV, gnstepsize = 1, stepBack = 0;
if (setting_trace_GNIterations > 0) bestEnergy = 1e5;
int gnStepGood = 0, gnStepBad = 0;
for (int it = 0; it < setting_trace_GNIterations; it++)
{
float H = 1, b = 0, energy = 0;
for (int idx = 0; idx < patternNum; idx++)
{
Vec3f hitColor = getInterpolatedElement33(frame->dI,
(float)(bestU + rotatePattern[idx][0]),
(float)(bestV + rotatePattern[idx][1]), wG[0]);
if (!std::isfinite((float)hitColor[0])) {energy += 1e5; continue;}
float residual = hitColor[0] - (hostToFrame_affine[0] * color[idx] + hostToFrame_affine[1]);
float dResdDist = dx * hitColor[1] + dy * hitColor[2];
float hw = fabs(residual) < setting_huberTH ? 1 : setting_huberTH / fabs(residual);
H += hw * dResdDist * dResdDist;
b += hw * residual * dResdDist;
energy += weights[idx] * weights[idx] * hw * residual * residual * (2 - hw);
}
if (energy > bestEnergy)
{
gnStepBad++;
stepBack *= 0.5;
bestU = uBak + stepBack * dx;
bestV = vBak + stepBack * dy;
if (debugPrint)
printf("GN BACK %d: E %f, H %f, b %f. id-step %f. UV %f %f -> %f %f.\n",
it, energy, H, b, stepBack,
uBak, vBak, bestU, bestV);
}
else
{
gnStepGood++;
float step = -gnstepsize * b / H;
if (step < -0.5) step = -0.5;
else if (step > 0.5) step = 0.5;
if (!std::isfinite(step)) step = 0;
uBak = bestU;
vBak = bestV;
stepBack = step;
bestU += step * dx;
bestV += step * dy;
bestEnergy = energy;
if (debugPrint)
printf("GN step %d: E %f, H %f, b %f. id-step %f. UV %f %f -> %f %f.\n",
it, energy, H, b, step,
uBak, vBak, bestU, bestV);
}
if (fabsf(stepBack) < setting_trace_GNThreshold) break;
}到这一步,已经找到了亚像素级别的匹配点,也确定像素的匹配误差,接下来就是计算逆深度和逆深度不确定以便进一步的更新,这一步的代码如下。在深度估计以及不确定度计算这一小节已经详细的推导了深度及不确定度的计算,公式严格的根据代码变量进行表示,因此也就不多陈述了。
if (dx * dx > dy * dy)
{
idepth_min = (pr[2] * (bestU - errorInPixel * dx) - pr[0]) / (hostToFrame_kt[0] - hostToFrame_kt[2] * (bestU - errorInPixel * dx));
idepth_max = (pr[2] * (bestU + errorInPixel * dx) - pr[0]) / (hostToFrame_kt[0] - hostToFrame_kt[2] * (bestU + errorInPixel * dx));
}
else
{
idepth_min = (pr[2] * (bestV - errorInPixel * dy) - pr[1]) / (hostToFrame_kt[1] - hostToFrame_kt[2] * (bestV - errorInPixel * dy));
idepth_max = (pr[2] * (bestV + errorInPixel * dy) - pr[1]) / (hostToFrame_kt[1] - hostToFrame_kt[2] * (bestV + errorInPixel * dy));
}
if (idepth_min > idepth_max) std::swap<float>(idepth_min, idepth_max);此次记录完全是根据笔者自己的理解,也有很多地方理解得不是特别清楚,如有错误的地方,还望指正,欢迎交流。
转载请注明作者和出处(https://blog.csdn.net/waittingforyou12)
























 895
895

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








