https://zhuanlan.zhihu.com/p/41993080

一、什么是生成对抗网络
通俗的讲:
- 对抗网络有一个生成器(Generator),还有一个判别器 (Discriminator);
- 生成器从随机噪声中生成图片,由于这些图片都是生成器臆想出来的,所以我们称之为 Fake Image;
- 生成器生成的照片Fake Image和训练集里的Real Image都会传入判别器,判别器判断他们是 Real 还是 Fake。
那么我们如何训练网络呢?要达到什么样的目的?
- 我们希望生成器生成的图片足够真实,可以骗过判别器;
- 我们也希望判别器足够“精明”,可以很好的分别出真图还是生成图;
- 最后在训练中,生成器和判别器达到一种“对抗”中的平衡,结束训练。
这时,我们分离出 生成器,它便可以帮助我们“生成”想要的图片。
二、基本概念
生成图片并不是一个新出现的需求,但是因为GAN的引入变得非常火爆。对于需要深入研究深度学习的人来说,还是需要认真学习其数学原理。
首先我们介绍几个概念(这几个概念是相互继承的,需要理解相互之间的关系):
- 信息量
- 信息熵
- K-L散度
- 交叉熵
1、信息量
假设有离散型随机变量 x,其取值集合为 X;且 x 的概率分布为 P(x)。那么定义事件 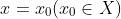 的信息量为:
的信息量为:
![]()
意义:对于小概率事件,其对应的信息量将会非常小;但是对于大概率事件,其包含的信息量就会很大。
2、信息熵
根据香浓信息熵公式,对任意一个随机变量 x,定义其信息熵为  ,单位为 bit,由于
,单位为 bit,由于 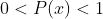 ,所以 H(x)>0。
,所以 H(x)>0。

信息熵可以简称为熵,代表了随机变量 x 的混乱程度。其实就是其信息量 I(x)的数学期望。熵越大,随机性越强。
通过简单的求导过程,我们可以发现熵是存在最大值的:
当一个随机变量 x 各取值的概率相等时,x 的无序混乱度最大,我们也就最难判断哪种情况容易放生,即熵最大!
3、KL散度:
参考博客:https://blog.csdn.net/wangdongwei0/article/details/83628438
4、交叉熵
参考博客:https://blog.csdn.net/wangdongwei0/article/details/83628438
三、生成图片的原理
1、基本原理
- 假设一组数据 x 服从概率分布
 ,记为
,记为 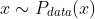
- 对于以 x 为输入的分布
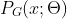 ,通过学习参数
,通过学习参数  使得
使得 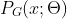 接近
接近  ,那么就可以找到一个生成器。
,那么就可以找到一个生成器。
那么如何学习参数呢?显然又到了使用最大似然估计的时候了。
2、最大似然估计
从 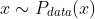 随机采集一组样本
随机采集一组样本 
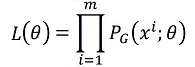
使得  取得最大值时的
取得最大值时的  即为我们想要的值:
即为我们想要的值:

注意到样本  来源自
来源自  ,所以:
,所以:

需要说明,公式中绿色横线项是一个  无关的常数项,所以减去后不会影响
无关的常数项,所以减去后不会影响  的结果。
的结果。
所以结论是:我们要找的  就是使得
就是使得  取得最小值的
取得最小值的  参数。
参数。
那如何来找这个  呢?
呢?
假设 是一个神经网络。
是一个神经网络。
首先随机一个向量  ,通过网络
,通过网络  生成图片
生成图片  ;那么我们如何比较两个分布是否相似呢?只要我们取一组sample
;那么我们如何比较两个分布是否相似呢?只要我们取一组sample  ,这组
,这组  符合一个分布,那么通过网络就可以生成另一个分布
符合一个分布,那么通过网络就可以生成另一个分布 ,然后来比较与真实分布
,然后来比较与真实分布 。
。
由于神经网络可以拟合任意的函数,那么也可以拟合任意分布(包括  )。所以可以用正态分布,取样去训练一个神经网络,学习到一个很复杂的分布。
)。所以可以用正态分布,取样去训练一个神经网络,学习到一个很复杂的分布。
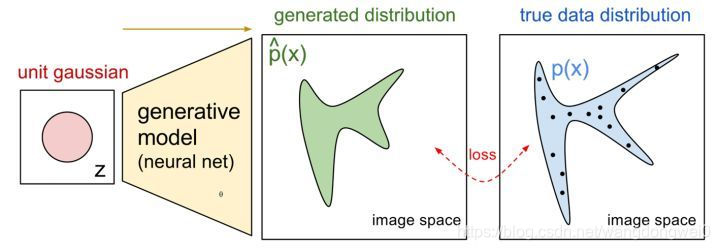
当给神经网络的输入时一个分布  ,它的输出也可以看做一个分布
,它的输出也可以看做一个分布  。那么这个过程可以看作:
。那么这个过程可以看作:
![P_G(x)=\int_{z}^{}P_{prrior}(z)I_{[G(z)=x]}dz\\](https://i-blog.csdnimg.cn/blog_migrate/29f15b61649a49e3550e5dd06a471685.png%28x%29%3D%5Cint_%7Bz%7D%5E%7B%7DP_%7Bprrior%7D%28z%29I_%7B%5BG%28z%29%3Dx%5D%7Ddz%5C%5C)
其中 ![I_{[G(z)=x]}](https://i-blog.csdnimg.cn/blog_migrate/251ec9823e54495090246522e74a1d8c.png) 代表神经网络输入
代表神经网络输入  时,输出恰好为
时,输出恰好为  。
。
但此时如果使用最大似然估计会存在问题,就是神经网络的参数量太大,想要计算似然(likelihood)来对神经网络的参数进行估计是不现实的。
所以生成对抗网络GAN的最大贡献,就是用神经网络黑盒代替了上述过程:
用Gernerator代替  ,用Discriminator代替
,用Discriminator代替  去约束Gernerator,不再需要似然估计,用玄学战胜了困难。
去约束Gernerator,不再需要似然估计,用玄学战胜了困难。
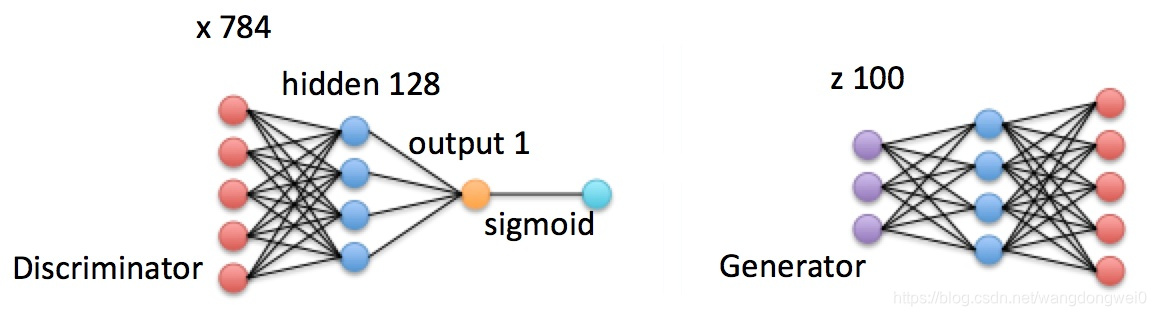
- Generator(G)
所谓的生成器,就是将  大小的随机噪声
大小的随机噪声  通过全连接上采样到
通过全连接上采样到  大小的图片(mnist图片大小)。设随机噪声
大小的图片(mnist图片大小)。设随机噪声  服从
服从  分布,即
分布,即 。那么生成器的输出可以表示为
。那么生成器的输出可以表示为  。
。
- Discriminator(D)
所谓判别器,其实就是一个全连接分类网络,输入为  大小的图片,记为
大小的图片,记为 。输出由于经过sigmoid,所以
。输出由于经过sigmoid,所以  是一个
是一个  之间的常数,代表输入
之间的常数,代表输入  为数字图片的概率。
为数字图片的概率。
定义GAN的Cost value如下:
![V(D,G)=E_{x\sim P_{data}(x)}\left[ \log D(x) \right]+E_{z\sim P_z(z)}\left[\log (1-D(G(z))) \right]\\](https://i-blog.csdnimg.cn/blog_migrate/551d275cf34259b2245527105f044342.png)
那么希望找到的Generator是:

如何理解  ?首先来感性的认识下
?首先来感性的认识下 
判别器是一个二分类模型,判断输入的图片是Real image or Fake image。
假定判别器  输入
输入 ,对应label为
 ,则交叉熵为:
,则交叉熵为:

当有  个样本
个样本  时
时  之和为:
之和为:

考虑这里的样本 来源:
- 假设以
 的概率
的概率 来自Real image,其中
;
- 即对应
 概率
概率 来自Fake image,其中
 。
。
那么:


当  采样足够多时,多到能够代表样本分布时:
采样足够多时,多到能够代表样本分布时:
![sum(CE)=-E_{x\sim P_{data}(x)}\left[ \log D(x) \right]-E_{z\sim P_z(z)}\left[\log (1-D(G(z))) \right]\\](https://i-blog.csdnimg.cn/blog_migrate/92d6c14c51155373e41bbbb53afbf06a.png)
即:


- 训练
 ,使得
,使得  变大,即交叉熵和KL散度变小
变大,即交叉熵和KL散度变小 - 训练
 ,使得
,使得  变小,即交叉熵和KL散度变大
变小,即交叉熵和KL散度变大
最终在  的博弈中整个GAN系统趋向于平衡。
的博弈中整个GAN系统趋向于平衡。
关于  原理的数学证明(数学公式预警)
原理的数学证明(数学公式预警)
首先考虑在给定  的情况下
的情况下 的含义。
的含义。
![V(D,G)=E_{x\sim P_{data}(x)}\left[ \log D(x) \right]+E_{z\sim P_z(z)}\left[\log (1-D(G(z))) \right]](https://i-blog.csdnimg.cn/blog_migrate/ddfa0b3df3e3b4652d18790f2694d624.png%3DE_%7Bx%5Csim+P_%7Bdata%7D%28x%29%7D%5Cleft%5B+%5Clog+D%28x%29+%5Cright%5D%2BE_%7Bz%5Csim+P_z%28z%29%7D%5Cleft%5B%5Clog+%281-D%28G%28z%29%29%29+%5Cright%5D)


![=\int_{x}^{}\left[ P_{data}(x)\log D(x)+P_G(x)\log(1-D(x)) \right]dx](https://i-blog.csdnimg.cn/blog_migrate/8eb95ee17b3c304c4f2b6eb8d028f380.png)
当每一个  取得最大值时,
取得最大值时,  也取得最大值。
也取得最大值。
观察函数  ,在
,在  取得最大值(不信你自己算)。所以:
取得最大值(不信你自己算)。所以:

在给定  时,
时,  使
使  取得最大值。
取得最大值。
然后将  带入
带入  :
:
![\max_DV(D,G)=E_{x\sim P_{data}(x)}\left[\log D^*(x)\right]+E_{z\sim P_z(z)} \left[ \log(1-D^*(G(z))) \right]](https://i-blog.csdnimg.cn/blog_migrate/690674ca77da97d2f02dcc6864c1f78c.png%3DE_%7Bx%5Csim+P_%7Bdata%7D%28x%29%7D%5Cleft%5B%5Clog+D%5E%2A%28x%29%5Cright%5D%2BE_%7Bz%5Csim+P_z%28z%29%7D+%5Cleft%5B+%5Clog%281-D%5E%2A%28G%28z%29%29%29+%5Cright%5D)
![=E_{x\sim P_{data}(x)}\left[\log D^*(x)\right]+E_{x\sim P_G(x)} \left[ \log(1- D^*(x)) \right]](https://i-blog.csdnimg.cn/blog_migrate/c70b8f15d1f689ff790dda052bcd517c.png)
![=E_{x\sim P_{data}(x)}\left[\log \frac{P_{data}(x)}{P_{data}(x) + P_G(x)}\right]+E_{x\sim P_G(x)} \left[ \log(\frac{P_{G}(x)}{P_{data}(x) + P_G(x)}) \right]](https://i-blog.csdnimg.cn/blog_migrate/d424178965d38ed0c438b927689a1089.png)


在  固定的情况下,当通过训练
固定的情况下,当通过训练  使得
使得  ,即
,即  生成的图片与真实图片非常接近的情况下获得
生成的图片与真实图片非常接近的情况下获得  。
。
看到这,GAN的训练过程就是小菜一碟了。

整个训练过程简单说就是交替下面的过程:
- 固定
 中所有参数,收集Real image + Fake image,用梯度下降法修正
中所有参数,收集Real image + Fake image,用梯度下降法修正 
- 然后固定
 中所有参数,收集Fake image,用梯度下降法修正
中所有参数,收集Fake image,用梯度下降法修正 
条件生成对抗网络CGAN(Conditional Generative Adversarial Nets)
OK,了解了GAN的基本原理后,就可以生成数字了。但是有一个问题,GAN生成的数字是完全随机的,即具体生成  中的哪一个数字依赖于随机输入
中的哪一个数字依赖于随机输入  。
。
那么如果只想固定生成某个具体数字怎么办?这时就要用到CGAN网络了。
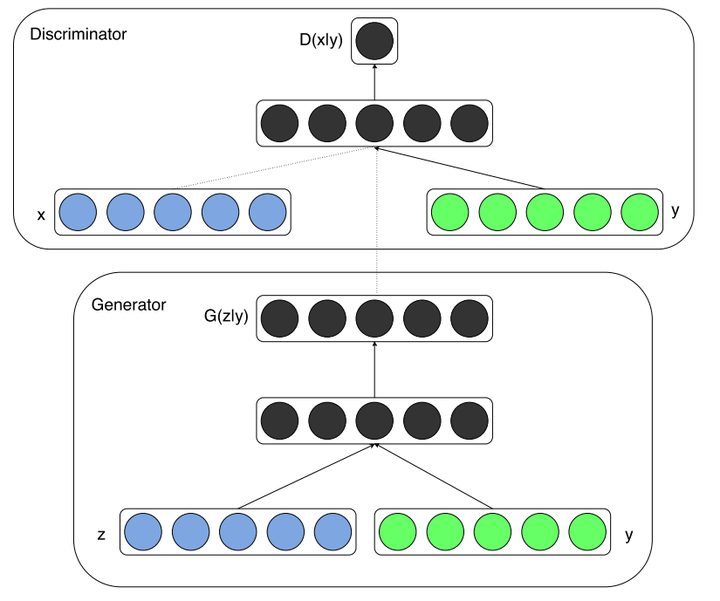
定义CGAN:
Generator为  ,代表输入噪声
,代表输入噪声 和标签
和标签  的情况下生成的特定
的情况下生成的特定  类别图片。
类别图片。
Discrimiator为 ,代表输入输入图片
,代表输入输入图片  经过判别后是
经过判别后是  类别的概率。
类别的概率。
同时  如下:
如下:
![V(D,G)=E_{x\sim P_{data}(x)}\left[ \log D(x|y) \right]+E_{z\sim P_z(z)}\left[\log (1-D(G(z|y))) \right]\\](https://i-blog.csdnimg.cn/blog_migrate/ddfa0b3df3e3b4652d18790f2694d624.png%3DE_%7Bx%5Csim+P_%7Bdata%7D%28x%29%7D%5Cleft%5B+%5Clog+D%28x%7Cy%29+%5Cright%5D%2BE_%7Bz%5Csim+P_z%28z%29%7D%5Cleft%5B%5Clog+%281-D%28G%28z%7Cy%29%29%29+%5Cright%5D%5C%5C)
要寻找的  如下:
如下:

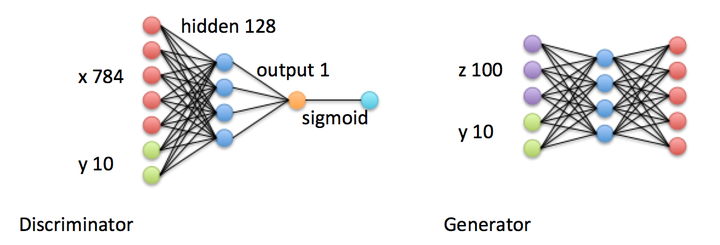
相比于原始GAN,其实就是多了个类别标签  ,并将原来的2分类变为多分类。
,并将原来的2分类变为多分类。
那么这个  是什么?也许是个矩阵,反正每个类别有自己特定的
是什么?也许是个矩阵,反正每个类别有自己特定的  ,只需要将
,只需要将  与
与  拼接或相加在一起就能形成
拼接或相加在一起就能形成  了(当然必须保证
了(当然必须保证  的生成方式,训练和评测时是一样的)。
的生成方式,训练和评测时是一样的)。
还没有懂CGAN?建议你看看代码吧:GAN Code
参考文献:
[1] Agustinus Kristiadi's Blog (GitHub stars 3k+)
Generative Adversarial Nets in TensorFlow
Conditional Generative Adversarial Nets in TensorFlow
[2] 李宏毅深度学习课程
Machine Learning and having it deep and structured (2017,Spring)








 本文深入浅出地介绍了生成对抗网络(GAN)的工作原理,包括生成器和判别器的交互机制,以及如何通过对抗训练达到生成高质量图片的目的。此外,还详细解释了信息熵、KL散度和交叉熵等关键概念,帮助读者理解GAN背后的数学原理。
本文深入浅出地介绍了生成对抗网络(GAN)的工作原理,包括生成器和判别器的交互机制,以及如何通过对抗训练达到生成高质量图片的目的。此外,还详细解释了信息熵、KL散度和交叉熵等关键概念,帮助读者理解GAN背后的数学原理。
















 941
941

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








