前言
本博文适合有一定立体几何基础的学生自学使用。
典例剖析
【2024高一数学必修二训练题】如图,已知正方体 A B C D − A 1 B 1 C 1 D 1 ABCD-A_1B_1C_1D_1 ABCD−A1B1C1D1,点 P P P 在面对角线 B C 1 BC_1 BC1 上运动,则下列四个结论:① 三棱锥 A − D 1 P C A-D_1PC A−D1PC 的体积不变;② A 1 P / / A_1P// A1P// 平面 A C D 1 ACD_1 ACD1;③ D P ⊥ B C 1 DP\perp BC_1 DP⊥BC1;④ 平面 P D B 1 ⊥ PDB_1\perp PDB1⊥ 平面 A C D 1 ACD_1 ACD1 . 其中正确的序号为__________ ;①②④ ;
解析:由于容易发现 B C 1 / / A D 1 BC_1//AD_1 BC1//AD1,故当点 P P P 在面对角线 B C 1 BC_1 BC1 上运动时,点 P P P 到平面 A D 1 C AD_1C AD1C 的距离应该是定值,再结合下底面 A D 1 C AD_1C AD1C 的面积固定,则可知三棱锥 P − A D 1 C P-AD_1C P−AD1C 的体积不变,即三棱锥 A − D 1 P C A-D_1PC A−D1PC 的体积不变,故①正确;
证明②的正确的思路比较多:其一,连接 A 1 B A_1B A1B, A 1 C 1 A_1C_1 A1C1,则容易知道平面 A D 1 C / / AD_1C// AD1C// 平面 A 1 B C 1 A_1BC_1 A1BC1,故当点 P P P 在面对角线 B C 1 BC_1 BC1 上运动时,直线 A 1 P ⊂ A_1P\subset A1P⊂ 平面 B A 1 C 1 BA_1C_1 BA1C1,故 A 1 P / / A_1P// A1P// 平面 A C D 1 ACD_1 ACD1;其二,特殊位置法,分别让点 P P P 移动到点 B B B 和点 C 1 C_1 C1,在这两个特殊位置时都可以说明 A 1 P / / A_1P// A1P// 平面 A C D 1 ACD_1 ACD1,这样猜想当点 P P P 移动到其他位置时,一定有 A 1 P / / A_1P// A1P// 平面 A C D 1 ACD_1 ACD1;其三,在平面 A D 1 C AD_1C AD1C 中如何找这样的直线,过点 C C C 在平面 A D 1 C AD_1C AD1C 中做 C V / / A 1 P CV//A_1P CV//A1P,连接 A 1 V A_1V A1V,则四边形 A 1 P C V A_1PCV A1PCV 是平行四边形,故一定有 A 1 P / / A_1P// A1P// 平面 A C D 1 ACD_1 ACD1;故 ②正确;
对于③,采用特殊位置法,当点 P P P 移动到点 B B B 和点 C 1 C_1 C1, D P DP DP 和 B C 1 BC_1 BC1 都是面对角线,如果再连接 C 1 D C_1D C1D(或 B D BD BD),则 D P DP DP 和 B C 1 BC_1 BC1 的夹角为 6 0 ∘ 60^{\circ} 60∘,故③错误;
对于④,我们已经积累了体对角线 B 1 D ⊥ B_1D\perp B1D⊥ 平面 A D 1 C AD_1C AD1C,又 B 1 D ⊂ B_1D\subset B1D⊂ 平面 P D B 1 PDB_1 PDB1,则平面 P D B 1 ⊥ PDB_1\perp PDB1⊥ 平面 A C D 1 ACD_1 ACD1,故 ④正确,
综上所述, ①②④ 正确;
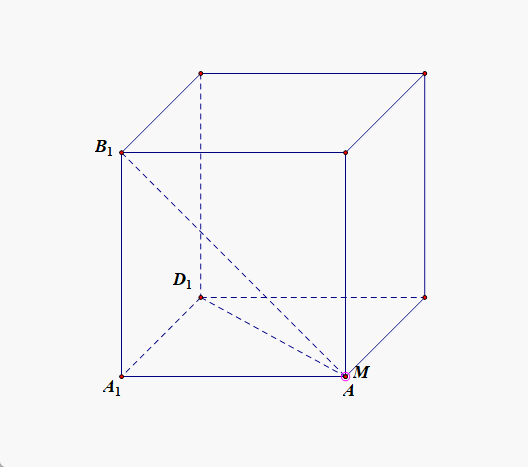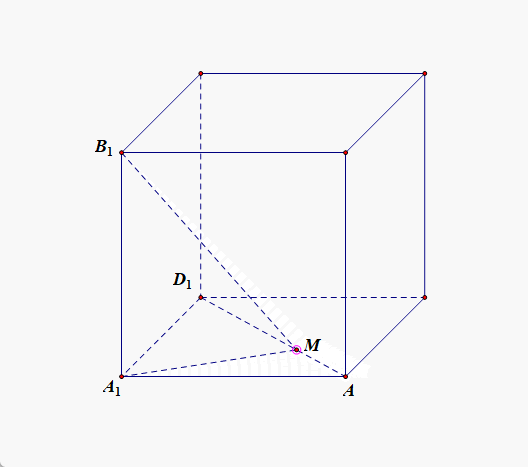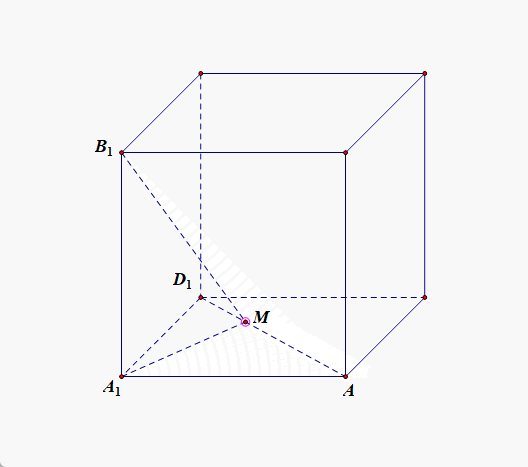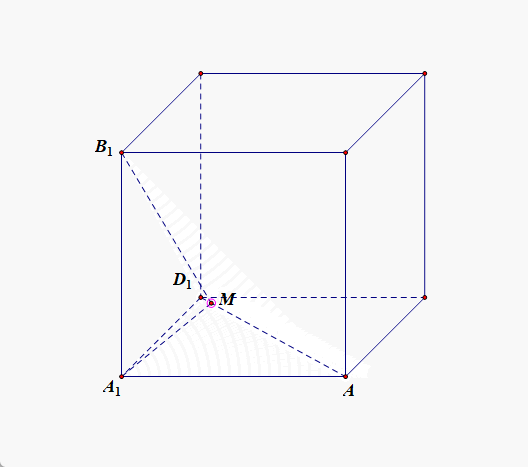
【2024高一训练题目】如图,点 M M M 是棱长为 1 1 1 的正方体 A B C D − A 1 B 1 C 1 D 1 ABCD-A_1B_1C_1D_1 ABCD−A1B1C1D1 中的侧面 A D D 1 A 1 ADD_1A_1 ADD1A1 上的一个动点(包含边界),则下列结论正确的是【 \qquad 】

A.有无数个点 M M M 满足 C M ⊥ A D 1 CM\perp AD_1 CM⊥AD1;
B.当点 M M M 在棱 D D 1 DD_1 DD1 上运动时, M A + M B 1 MA+MB_1 MA+MB1 的最小值为 3 + 1 \sqrt{3}+1 3+1;
C.若 M B 1 = 2 MB_1=\sqrt{2} MB1=2,则动点 M M M 的轨迹长度为 π 2 \cfrac{\pi}{2} 2π;
D.在线段 A D 1 AD_1 AD1 上存在点 M M M ,使异面直线 M B 1 MB_1 MB1 与 C D CD CD 所成的角是 3 0 ∘ 30^{\circ} 30∘;
解:对于选项 A A A,当点 M M M 在线段 A 1 D A_1D A1D 上运动时,容易证明 C M ⊥ A D 1 CM\perp AD_1 CM⊥AD1;由于 A D 1 ⊥ A 1 D AD_1\perp A_1D AD1⊥A1D, A D 1 ⊥ C D AD_1\perp CD AD1⊥CD,
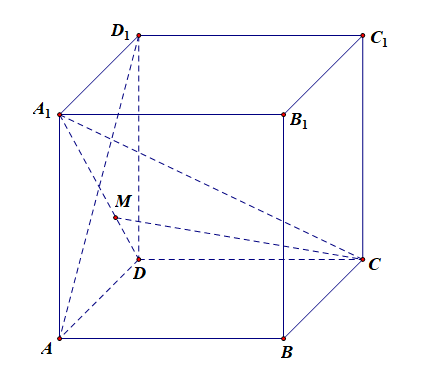
所以 A D 1 ⊥ AD_1\perp AD1⊥ 平面 A 1 C D A_1CD A1CD, C M ⊂ CM\subset CM⊂ 平面 A 1 D C A_1DC A1DC,故 A D 1 ⊥ C M AD_1\perp CM AD1⊥CM,即有无数个点 M M M 满足 C M ⊥ A D 1 CM\perp AD_1 CM⊥AD1,故选项 A A A 正确;
对于选项 B B B,当点 M M M 在棱 D D 1 DD_1 DD1 上运动时, M A + M B 1 MA+MB_1 MA+MB1 是两条折线长度的和,而我们知道,在一个平面内两点之间线段最短,故需要将正方体展开,使得点 A A A 和点 B 1 B_1 B1 以及点 M M M 三点共面, 要使得 M A + M B 1 MA+MB_1 MA+MB1 最小,只需要那三点共线即可。为此,我们将侧面 A D D 1 A 1 ADD_1A_1 ADD1A1 以 D D 1 DD_1 DD1 为轴,顺时针旋转 13 5 ∘ 135^{\circ} 135∘,使得旋转后的平面 A D D 1 A 1 ADD_1A_1 ADD1A1 与平面 B D D 1 B 1 BDD_1B_1 BDD1B1 共面,连接 A B 1 AB_1 AB1 与 D D 1 DD_1 DD1 相交于点 M M M,此时线段 A B 1 AB_1 AB1 的长度就是 M A + M B 1 MA+MB_1 MA+MB1 的最小值,如图所示,
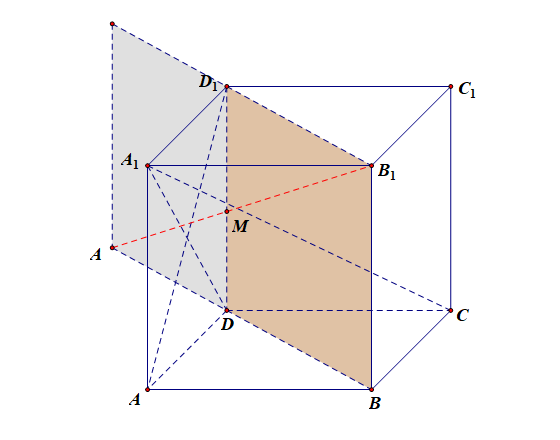
此时, A B 1 2 AB_1^2 AB12 = = = A B 2 + B B 1 2 AB^2+BB_1^2 AB2+BB12,即 A B 1 AB_1 AB1 = = = 1 2 + ( 1 + 2 ) 2 \sqrt{1^2+(1+\sqrt{2})^2} 12+(1+2)2 = = = 4 + 2 2 \sqrt{4+2\sqrt{2}} 4+22 ≠ \neq = 3 + 1 = \sqrt{3}+1= 3+1= ( 3 + 1 ) 2 = 4 + 2 3 \sqrt{(\sqrt{3}+1)^2}=\sqrt{4+2\sqrt{3}} (3+1)2=4+23,故选项 B B B 错误;
对于选项 C C C,连接 A 1 M A_1M A1M 和 B 1 M B_1M B1M,在 R t △ A 1 B 1 M Rt\triangle A_1B_1M Rt△A1B1M 中, A 1 B 1 = 1 A_1B_1=1 A1B1=1, B 1 M = 2 B_1M=\sqrt{2} B1M=2,

由勾股定理可知, A 1 M = 1 A_1M=1 A1M=1,由于点 M M M 在平面 A D D 1 A 1 ADD_1A_1 ADD1A1 内运动,且 A 1 M = 1 A_1M=1 A1M=1,故点 M M M 的轨迹为以点 A 1 A_1 A1 为圆心,以 1 1 1 为半径的四分之一个圆周(在平面 A D D 1 A 1 ADD_1A_1 ADD1A1 内),故所求轨迹长度为 1 4 × 2 π × 1 = π 2 \cfrac{1}{4}\times 2\pi\times 1=\cfrac{\pi}{2} 41×2π×1=2π,故选项 C C C 正确;
对于选项 D D D ,采用计算的方法,由于棱长 A 1 B 1 = 1 A_1B_1=1 A1B1=1,令 ∠ A 1 B 1 M = θ \angle A_1B_1M=\theta ∠A1B1M=θ,则 tan θ = A 1 M A 1 B 1 = A 1 M \tan\theta=\cfrac{A_1M}{A_1B_1}=A_1M tanθ=A1B1A1M=A1M,由于 y = tan x y=\tan x y=tanx 在 [ 0 , π 2 ) [0,\cfrac{\pi}{2}) [0,2π) 内单调递增,故 A 1 M A_1M A1M 最小时,角 θ \theta θ 最小,接下来关键是确定何时 A 1 M A_1M A1M 最小;问题转化为直线外一点到直线上的任意一点的点点距离何时最小,我们知道直线外一点到直线上的任意一点的连线中,只有垂线段最短,即当 A 1 M A_1M A1M ⊥ \perp ⊥ A D 1 AD_1 AD1 时满足条件,由图形的特殊性可知,当点 M M M 为线段 A D 1 AD_1 AD1 的中点时 A 1 M A_1M A1M 最短,此时 A 1 M = 2 2 A_1M=\cfrac{\sqrt{2}}{2} A1M=22,即 tan θ \tan\theta tanθ = = = A 1 M A_1M A1M = = = 2 2 \cfrac{\sqrt{2}}{2} 22 > > > 3 3 \cfrac{\sqrt{3}}{3} 33 = = = tan 3 0 ∘ \tan30^{\circ} tan30∘,故 θ \theta θ 的最小值大于 3 0 ∘ 30^{\circ} 30∘ ,即在线段 A D 1 AD_1 AD1 上不存在点 M M M ,使异面直线 M B 1 MB_1 MB1 与 C D CD CD 所成的角是 3 0 ∘ 30^{\circ} 30∘,故选项 D D D 错误;
综上所述,选 A C AC AC ;
【2024高一训练题目】如图,在正方体 A B C D − A 1 B 1 C 1 D 1 ABCD-A_1B_1C_1D_1 ABCD−A1B1C1D1 中,点 F F F 是线段 B C 1 BC_1 BC1 上的动点,则直线 A 1 F A_1F A1F 与平面 B D C 1 BDC_1 BDC1 所成的最大角的余弦值为___________.

解:如图所示,利用正方体中储备的知识 1很容易想到,连接 A 1 C A_1C A1C,则可知体对角线 A 1 C ⊥ A_1C\perp A1C⊥ 平面 B C 1 D BC_1D BC1D,令垂足为点 O O O,连接 O F OF OF ,则直线 A 1 F A_1F A1F 与平面 B D C 1 BDC_1 BDC1 所成的角为 ∠ A 1 F O \angle A_1FO ∠A1FO,为了求 ∠ A 1 F O \angle A_1FO ∠A1FO 的最大值,可以考虑两个角度:其一,从形上思考,在等边 △ D C 1 B \triangle DC_1B △DC1B 中,当动点 F F F 靠近点 B B B 或点 C 1 C_1 C1 时 ∠ A 1 F O \angle A_1FO ∠A1FO 越来越小(可以借助极端的情形思考,让线段 B C 1 BC_1 BC1 非常长,则角的顶点就近乎在无限远处,其大小就接近 0 了),那么在线段的中点位置时[其实是 O F ⊥ B C 1 OF\perp BC_1 OF⊥BC1 时,为什么这样可以从思路二中得到解答和印证], ∠ A 1 F O \angle A_1FO ∠A1FO 达到最大,为便于计算,令 A B = 1 AB=1 AB=1,则 A 1 C = 3 A_1C=\sqrt{3} A1C=3, A 1 O A_1O A1O = = = 2 3 A 1 C \cfrac{2}{3}A_1C 32A1C = = = 2 3 3 \cfrac{2\sqrt{3}}{3} 323, B D BD BD = = = 2 \sqrt{2} 2,则 B F BF BF = = = 2 2 \cfrac{2}{2} 22, D F DF DF = = = 6 2 \cfrac{6}{2} 26,则 O F OF OF = = = 1 3 D F \cfrac{1}{3}DF 31DF = = = 6 6 \cfrac{\sqrt{6}}{6} 66,又由 R t △ A 1 B 1 F Rt\triangle A_1B_1F Rt△A1B1F 可得 A 1 F A_1F A1F = = = 6 2 \cfrac{\sqrt{6}}{2} 26,故 cos ∠ A 1 F O \cos\angle A_1FO cos∠A1FO = = = O F A 1 F \cfrac{OF}{A_1F} A1FOF = = = 1 3 \cfrac{1}{3} 31;

其二,从数上思考,由上述可知所求的线面角为 ∠ A 1 F O \angle A_1FO ∠A1FO,在 R t △ A 1 F O Rt\triangle A_1FO Rt△A1FO 中,由于 A 1 O A_1O A1O 的长度为定值,故可设 A 1 O A_1O A1O = = = a a a, O F OF OF = = = x x x,则 A 1 F A_1F A1F = = = x 2 + a 2 \sqrt{x^2+a^2} x2+a2,这样 cos ∠ \cos\angle cos∠ A 1 F O A_1FO A1FO = = = O F A 1 F \cfrac{OF}{A_1F} A1FOF = = = x x 2 + a 2 \cfrac{x}{\sqrt{x^2+a^2}} x2+a2x = = = x 2 x 2 + a 2 \sqrt{\cfrac{x^2}{x^2+a^2}} x2+a2x2 = = = x 2 + a 2 − a 2 x 2 + a 2 \sqrt{\cfrac{x^2+a^2-a^2}{x^2+a^2}} x2+a2x2+a2−a2 = = = 1 − a 2 x 2 + a 2 \sqrt{1-\cfrac{a^2}{x^2+a^2}} 1−x2+a2a2.
由于 a a a 为常数,故当 x > 0 x>0 x>0 时, x ↗ x\nearrow x↗, x 2 ↗ x^2\nearrow x2↗, x 2 + a 2 ↗ x^2+a^2\nearrow x2+a2↗, a 2 x 2 + a 2 ↘ \cfrac{a^2}{x^2+a^2}\searrow x2+a2a2↘, − a 2 x 2 + a 2 ↗ -\cfrac{a^2}{x^2+a^2}\nearrow −x2+a2a2↗, 1 − a 2 x 2 + a 2 ↗ 1-\cfrac{a^2}{x^2+a^2}\nearrow 1−x2+a2a2↗, 1 − a 2 x 2 + a 2 ↗ \sqrt{1-\cfrac{a^2}{x^2+a^2}}\nearrow 1−x2+a2a2↗,故当 x ↗ x\nearrow x↗, cos ∠ \cos\angle cos∠ A 1 F O ↗ A_1FO\nearrow A1FO↗,又由于 y = cos x y=\cos x y=cosx 为 [ 0 , π 2 ] [0,\cfrac{\pi}{2}] [0,2π] 上的减函数,故如果要 ∠ \angle ∠ A 1 F O A_1FO A1FO 最大,则需要 cos ∠ \cos\angle cos∠ A 1 F O A_1FO A1FO 最小,即需要 x x x 最小,这样就需要 O F OF OF 最小,而直线外一点和直线上的动点之间的点点距中只有垂线段最短,故需要 O F ⊥ B C 1 OF\perp BC_1 OF⊥BC1, 依托思路一求得 A 1 O = 2 3 3 A_1O=\cfrac{2\sqrt{3}}{3} A1O=323, O F OF OF = = = 6 6 \cfrac{\sqrt{6}}{6} 66,代入求得 cos ∠ A 1 F O \cos\angle A_1FO cos∠A1FO = = = O F A 1 F \cfrac{OF}{A_1F} A1FOF = = = 1 3 \cfrac{1}{3} 31;
比如,积累正方体中体对角线 A 1 C ⊥ A_1C\perp A1C⊥ 平面 B C 1 D BC_1D BC1D,且知道 A 1 O = 2 3 A 1 C A_1O=\cfrac{2}{3}A_1C A1O=32A1C,等等,数学学习中的好多东西是需要积累的; ↩︎
























 959
959

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










