Tracking算法：Discriminative Correlation Filter (DCF)

基本框架

Minimum Output Sum of Squared Error Filter (MOSSE)

t个目标区域样本分别为$f_1,f_2,\cdots,f_t$，通过滤波器$h_t$，期望输出$g_i$（通常为二维高斯函数，峰值位于目标区域中心），最小化均方误差：

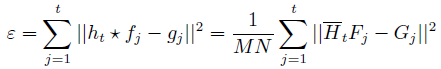
对$H_t$求导，令导数为0，得：

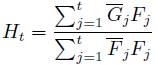
对于t+1帧，假设其在第t帧的目标区域内提取得到特征图z，那么计算$h_t$与z的相关值

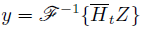
y的最大值的位置即被认为是t+1帧中目标区域的中心点.
我们保持目标区域尺寸不变，将其中心点进行移动相应位置，就得到了在新帧中的目标区域。对该区域进行特征提取，然后加入到训练集中对模型进行更新得到$h_{t+1}$后，即可进行下一帧
中的目标检测了。

在实际的tracking过程中，一般使用如下方法来更新模型:

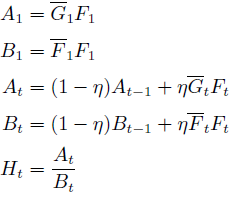
其中$\eta$为学习率。

缺点

• 只使用了灰度作为特征，模型所使用的特征维数太低，难以很好地反映目标的特性。
• 只估算了目标区域中心点在帧间的平移运动，而没有考虑目标在运动过程中反映在画面上的尺度变化，在目标尺度发生改变时难以适应。

Discriminative Scale Space Tracking Filter (DSST)

对MOSSE的改进：

• 使用fHoG替代灰度（通常fHoG为31dims，而DSST实际使用28dims）
• 考虑目标尺度变化

不考虑尺度变化

设特征维数为d，则特征图可记作$f^l, l=1,2,\cdots,d$。滤波器应和特征图匹配，误差函数：

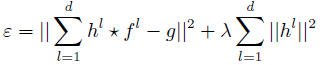
引入$\lambda$项是为了控制滤波器频域参数求解过程中的除0，另一方面也可以控制滤波器参数变化范围，$\lambda$越小，滤波器参数变化范围越大。
对上式做傅里叶变换，求导，令导数为0，得：

在实际操作中，可以用下式更新模型：

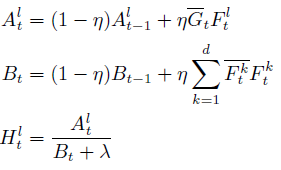
新帧预测：

考虑尺度变化

滤波器和特征图由$d\times M\times N$改为$d\times M\times N\times S$，S = num of scales，即构造金字塔。这导致复杂度增大为 O(dMNS×logMNS)