Tracking算法学习之Compressive Tracking——Real-Time Compressive Tracking

原文地址：【http://www4.comp.polyu.edu.hk/~cslzhang/CT/CT.htm】

部分理解借鉴于【http://blog.csdn.net/zouxy09/article/details/8118360】

一个很好的解读：【https://zhuanlan.zhihu.com/p/25312390】
本文的主要思想是：首先利用符合压缩感知RIP条件的随机感知矩阵对多尺度图像特征进行降维，然后再降维的特征上采用简单的朴素贝叶斯分类器进行分类。

主要思路如下：
（1）在第t帧的时候，采样得到若干张目标（正样本）和背景（负样本）的图像片，然后对他们进行多尺度变换。再通过一个稀疏测量矩阵对生成的多尺度图像特征进行降维，然后通过降维后的特征（包括目标和背景，属二分问题）去训练朴素贝叶斯分类器。
（2）在t+1帧的时候，我们在上一帧跟踪到的目标位置的周围采样n个扫描窗口（避免去扫描整幅图像），通过同样的稀疏测量矩阵对其降维，提取特征，然后用第t帧训练好的朴素贝叶斯分类器进行分类，分类分数最大的窗口就认为是目标窗口。
这样就实现了从t帧到t+1帧的目标跟踪。

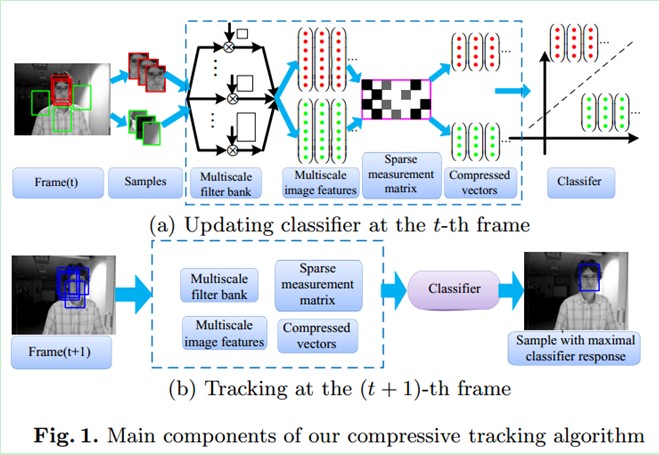
文章中提到的几个重要概念：
压缩感知：
压缩感知是一种数据获取和采样理论，该理论指出：如果信号是稀疏的或者在某个变换域是稀疏的，则可用一个测量矩阵将该信号投影到低维空间，投影后的低维信号包含了重构原始信号的全部信息，通过求解一个优化问题就可以从这些少量的投影中精确构建出原始信号。

RIP：有限等距性
1.随机投影：
对于一个高维空间的向量x（m维），使用一个随机矩阵R（nxm维），将其降维至低维空间向量v（n维），n远远小于m。表达式为v=R**x**。
文中提及Johnson-Lindenstrauss推论表明：可以随机选择一个适当的高维子空间（当然，需要比原始空间维度小），原始空间两点间的距离投影到这个子空间，能够高概率保留这种概率关系。（k+1次测量足以精确复原N维空间的k-稀疏信号。）而Baraniuk证明了满足J-L推论的随机矩阵同样满足压缩感知理论中的有限等距性（RIP）。因此，如果随机矩阵R满足J-L理论，并且如果x是可压缩的（或者说是稀疏的），那么晚我们就可以通过最小化误差来从v中高概率重构x。

2.随机测量矩阵：
一个比较典型的满足RIP条件的测量矩阵是随机高斯矩阵。对于矩阵R中的每一个元素r[i][j],均满足N（0，1）。但是，如果矩阵的维数m比较大的话，对于算法的存储和计算量都是较大的考验。因此，本文采用了一个非常稀疏的测量矩阵，定义如下：

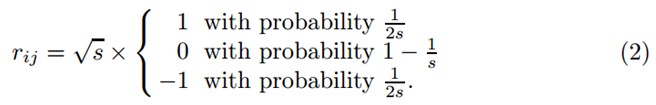
在s取值2或者3的情况下，能够满足J-L理论。因为只需要一个随机数生成器，所以上式的计算非常简单。当s取值m/log(m)（m为x的维度）时，生成的随机投影的精度可以近似随机高斯矩阵产生的随机投影。
在本文中，选取s=m/4，生成一个非常稀疏的随机矩阵。对于矩阵R的每一行，只需要计算c个元素的值，c<4。因此，时间复杂度很小。此外，只需要存储R的非零元素，所需存储空间也很小。

3.提出的算法：

假设在第一帧中已经选定了目标窗口。对于之后的每一模板帧，在当前目标位置的周围随机选取一些窗口，作为正样本，远离目标位置的地方随机选取一些窗口作为负样本，然后生成分类器。对于下一帧中的预测位置，在当前目标处选取一些窗口样本，分类分数最高的则为目标所在。

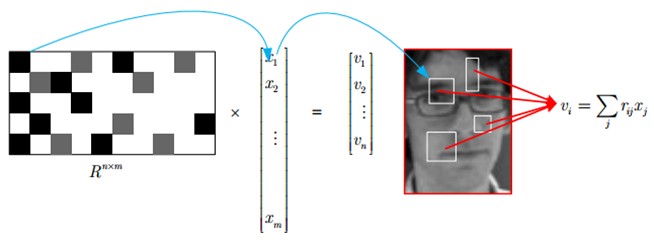
上图表示一个nxm的稀疏矩阵，即我们在2里生成的测量矩阵。他可以将一个高维图像空间的x（m维）变换到一个低维的空间v，即v=R**x**。
其中，矩阵R中，黑色、灰色和白色分别代表矩阵元素为负数、正数和零。蓝色箭头表示测量矩阵R的一行的一个非零元素感知x中的一个元素，等价于一个方形窗口滤波器和输入图像某一固定位置的灰度卷积。
为了实现尺度不变性，对每一个样本z∊R（wxh维），通过将其与一系列多尺度的矩形滤波器{h1,1,…,hw,h}进行卷积，每一种尺度的矩形滤波器定义如下：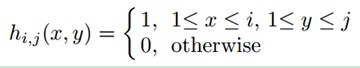
式中，i和j分别是矩形滤波器（模版）的宽和高。然后将滤波后的的图像矩阵展成一个wxh维的列向量。再将这些列向量连接成一个非常高维（(wxh)x(wxh)维）的多尺度图像特征向量x=(x1,…,xm)’。维数一般在10的6次方到10次方之间。
我们通过采用上面的稀疏随机矩阵R将x投影到低维空间的v。这个随机矩阵R只需要在程序启动时计算一次，然后在跟踪过程中保持不变。通过积分图，我们可以高效的计算v。

4.低维特征分析：
在低维特征空间v中的每个元素vi，都是不同尺度的空间分布特征的线性组合。由于测量矩阵R的稀疏可正可负，所以压缩特征可以像广义Haar-like特征一样计算相关灰度差。Haar-like特征计算比较耗时，通常是通过boosting算法选择重要特征来减少需要计算的特征数。在本文中，通过稀疏测量矩阵对这些数目庞大的Haar-like特征进行压缩，稀疏感知理论保证了压缩后的特征几乎保留了原有图像的所有信息，因此，我们可以直接对压缩空间里的投影特征进行分类，避免了维数灾难。

5.分类器的构建和更新：
对于每一个样本z（m维向量），他的低维表示是v（n维向量，n远小于m），假定v中的各元素是独立分布的。可以通过朴素贝叶斯分类器来建模。

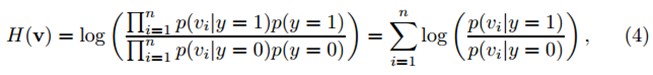
其中，y∊{0,1}代表样本标签，y=0表示负样本，y=1表示正样本，假设两个类的先验概率相等。p(y=1)=p(y=0)=0.5。Diaconis和Freedman证明了高维随机向量的随机投影几乎都是高斯分布的。因此，我们假定在分类器H(v)中的条件概率p(vi|y=1)和p(vi|y=0)也属于高斯分布，并且可以用四个参数来描述：

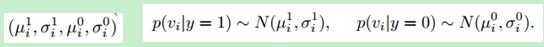
上式中的四个参数会进行增量更新：

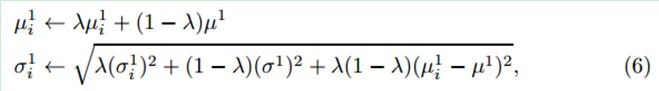
上式中的四个参数会进行增量更新：