note_三元量化中的Weight Grouping

读在前面：
三元量化中的 group 方法是指，通过逐渐增加全精度权重量化的比例来减小量化带来的误差。量化误差可以表达为：
$$\begin{array}{c}\Vert \mathbf{y}-{\mathbf{x}}^{\top }\mathbf{w}{\Vert }_2^2\le \Vert \mathbf{y}-{\mathbf{x}}^{\top }(r\mathbf{w}+(1-r)\mathbb{Q}(\mathbf{w})){\Vert }_2^2\\ \le \Vert \mathbf{y}-{\mathbf{x}}^{\top }\mathbb{Q}(\mathbf{w}){\Vert }_2^2,\end{array}$$其中，$r$ 控制着量化的比例。

本博客中文献笔记总结：

文献索引	量化精度	缩放因子求解	量化损失函数定义	增加精度方式	适用算法
一	多bit（$2$的幂次）	\	$E({\mathbf{W}}_l)=L({\mathbf{W}}_l)+\lambda R({\mathbf{W}}_l)$	重训练	CNN(all)
二	2/3 bit	$$\begin{gathered} {\alpha }_l=mean(W_l)+\beta max(W_l), \\ \beta =0.05 \end{gathered}$$	$L(W_l)+a_1{L}_p(W_l,\widehat{W_l})+a_{2}E(W_l,\widehat{W_l})$	重写量化损失+重训练	DNN
三	\	\	\	重训练	all
四	多bit	最小二乘法求解	$E_{x\sim \mathcal{N}(0,1),x>ϵ}[(Q_{ϵ}(x)-x{)}^2],\text{利用稀疏度}ϵ$ ∑ { α i } , { w ^ i T } ∥ y i T − Q ϵ ( α i w ^ i T X ) ∥ 2 2 \sum_{\{\alpha_i\},\{\hat{w}_i^T\}}\parallel y_i^T-Q_\epsilon(\alpha_i\hat{w}_i^TX)\parallel_2^2 ∑{αi​},{w^iT​}​∥yiT​−Qϵ​(αi​w^iT​X)∥22​	解耦量化“权重”和“激活”	DNN
五	3 bit	${\alpha }^{\ast }=({\sum }_{i\in I_{\Delta }}|{\mathbf{W}}_i|)/|I_{\Delta }|$	${\sum }_i\underset{{\alpha }_i,{\hat{\mathbf{W}}}^{(i)}}{\mathrm{argmin}}|{\mathbf{W}}^{(i)}-{\alpha }_i{\hat{\mathbf{W}}}^{(i)}{|}_F^2$	分组解析分析	all
六	3 bit	向后传播动态得到	\	pixel-wise和row-wise两种分组方式	DNN(CNN)
七	3 bit	NP问题，贪心策略	minimize ⁡ { x i } , { d i } , { y i } ∥ W − ∑ i k d i x i y i T ∥ F 2 \underset{{\{x_i\},\{d_i\},\{y_i\}}}{\operatorname{minimize}}\parallel W-\sum_i^kd_ix_iy_i^T\parallel_F^2 {xi​},{di​},{yi​}minimize​∥W−∑ik​di​xi​yiT​∥F2​	权重矩阵的不动点分解	all

下面是如下这篇综述中关于“Weight Grouping”部分引用文献的笔记：

作者综述笔记：Ternary Quantization: A Survey
原文链接：Ternary Quantization: A Survey

一、INCREMENTAL NETWORK QUANTIZATION: TOWARDS LOSSLESS CNNS WITH LOW-PRECISION WEIGHTS

Zhou A, Yao A, Guo Y, et al. Incremental network quantization: Towards lossless cnns with low-precision weights[J]. arXiv preprint arXiv:1702.03044, 2017.
ICLR 2017（此会虽无CCF等级，但是是人工智能顶会）

1. 动机和贡献

动机： 虽然 CNN 的量化已经取得了一些进步，但是依然面临着两个重要的问题：

• CNN量化过程中不可避免的精度损失；
• 与全精度权重训练模型相比，量化后模型需要增加更多轮数使得模型收敛。

贡献： 本文提出一种 incremental network quantization（INQ）CNN量化框架，在没有对CNN结构做出任何限制性假设的前提下，可以有效地将已经预训练好的全精度CNN模型（例如：32bit）转化为低精度模型（权重值限制到 $2$ 的幂次或者是 $0$）。相比于其他一次性将全部权重都进行量化的技术，本文通过考虑不同网络权重的重要程度不同，对其进行分批次的量化，主要包括如下几个步骤：

1. weight partition：将全精度权重分为两个互不相交的 “组group”；
2. group-wise quantization：将一个组中的权重量化，另一个组保持不变；
3. re-training：固定已量化后的组中的值，重新训练模型，改变另一个组中的值。

注：本文中将权重量化为 $2$ 的幂次或者是 $0$的目的是：将全精度权重的浮点数乘法运算变成二进制移位运算，以达到降低计算复杂度的作用。

2. 算法表示

2.2 weight partition

对于第 $l$ 层， weight partition 可以定义为：
A l ( 1 ) ∪ A l ( 2 ) = { W l ( i , j ) } , a n d   A l ( 1 ) ∩ A l ( 2 ) = ∅ , \mathbf{A}_{l}^{(1)}\cup\mathbf{A}_{l}^{(2)}=\{\mathbf{W}_{l}(i,j)\},\mathrm{and}~\mathbf{A}_{l}^{(1)}\cap\mathbf{A}_{l}^{(2)}=\emptyset, Al(1)​∪Al(2)​={Wl​(i,j)},and Al(1)​∩Al(2)​=∅,同时定义一个二元矩阵 ${\mathbf{T}}_l(i,j)$ 作为掩码，即：
$$\{\begin{array}{cc}{\mathbf{T}}_l(i,j)=0& \text{if}{\mathbf{W}}_l(i,j)\in {\mathbf{A}}_l^{(1)}\\ {\mathbf{T}}_l(i,j)=1& \text{if}{\mathbf{W}}_l(i,j)\in {\mathbf{A}}_l^{(2)}\end{array}$$

对于分组策略，本文中提出了两种方案：

• random partition：随机的将待分权重分成不相交的两个组；
• pruning-inspired partition：给一个以层为单位的阈值，绝对值大于此阈值的权重更有可能被分到同一组进行量化。（原因是：本文认为绝对值大的权重要性更大）

2.2 group-wise quantization: 使用变长编码的权重量化

假设 CNN 模型的权重可以表示为 { W l : 1 ≤ l ≤ L } \{{\mathbf{W}}_{l}:1\leq l\leq L\} {Wl​:1≤l≤L}，其中 ${\mathbf{W}}_l$ 表示第 $l$ 层权重值集合，$L$ 表示总层数；量化后低精度模型权重表示为 ${\hat{\mathbf{w}}}_l$，它的每一个元素取值都从集合 ${\mathbf{P}}_l$ 中选取：
P l = { ± 2 n 1 , ⋯   , ± 2 n 2 , 0 } , \mathbf{P}_l=\{\pm2^{n_1},\cdots,\pm2^{n_2},0\}, Pl​={±2n1​,⋯,±2n2​,0},其中，$n_1\ge n_2$ 是两个整数。

INQ 的量化规则为：
$${\hat{\mathbf{W}}}_l(i,j)=\{\begin{array}{ll}\beta \text{sgn}({\mathbf{W}}_l(i,j))& \text{if}(\alpha +\beta )/2\le \text{abs}({\mathbf{W}}_l(i,j))<3\beta /2\\ 0& \text{otherwise},\end{array}$$其中，$\alpha ,\beta$ 表示集合 ${\mathbf{P}}_l$ 中的相邻的两个元素。那么，如何得到集合 ${\mathbf{P}}_l$ 中的元素，即得到 $n_1,n_2$ 的值？首先，定义 $n_1$ 的取值为：
$$n_1=\text{floor}({\log }_2(4s/3)),$$其中，
$$s=\max (\mathrm{abs}({\mathbf{W}}_l)).$$因此，当确定量化维数 $b$ 后，可以得到 $n_2$ 的值为：
$$n_2=n_1+1-\frac{2^{(b-1)}}{2},$$下图是关于上述量化过程的一个示意图：

2.3 re-training

根据上面描述，重训练需要优化的如下目标函数：
$$\begin{array}{rl}\underset{{\mathbf{W}}_l}{\min }& E({\mathbf{W}}_l)=L({\mathbf{W}}_l)+\lambda R({\mathbf{W}}_l)\\ \text{s.t.}& {\mathbf{W}}_l(i,j)\in {\mathbf{P}}_l,\text{if}{\mathbf{T}}_l(i,j)=0,1\le l\le L,\end{array}$$其中，$L({\mathbf{W}}_l)$ 表示网络损失函数，$R({\mathbf{W}}_l)$ 表示正则项。因此，可以得到如下重训练规则：
$${\mathbf{W}}_l(i,j)\leftarrow {\mathbf{W}}_l(i,j)-\gamma \frac{\partial E}{\partial ({\mathbf{W}}_l(i,j))}{\mathbf{T}}_l(i,j),$$

综上，总算法流程图为：

二、Explicit Loss-Error-Aware Quantization for Low-Bit Deep Neural Networks

Zhou, Aojun, et al. “Explicit loss-error-aware quantization for low-bit deep neural networks.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2018.
CVPR 2018 CCF-A

1. 动机和贡献

动机： 现有关于DNN的二元/三元压缩存在测试精度低的问题，可能原因包括：

• 通过最小化 原始模型和量化后模型的差异 或者 输入与原始模型内积和输入与量化模型内积 这两种方式之一来量化模型；
• 很多策略都是一次性全部量化模型。

贡献： 本文提出一种基于最小化损失函数的量化技术（ELQ）来解决上述问题：

• 首先，同时考虑了 “近似误差” 和 “损失扰动” 的影响；
• 然后，通过增强策略，逐步量化模型参数（仿照“一”中思想）。

2. 主要算法

2.1 预备知识

向量函数的Taylor公式：
带积分余项的泰勒公式

0阶：
$$f(x)=f(x_0)+⟨{\int }_0^1\nabla f(x_0+\theta (x-x_0))\mathrm{d}\theta ,x-x_0⟩$$
1阶：
$$\begin{array}{rl}f(x)& =f(x_0)+⟨\nabla f(x_0),x-x_0⟩\\ & +⟨{\int }_0^1{\nabla }^{2}f(x_0+\theta (x-x_0))(1-\theta )\mathrm{d}\theta (x-x_0),x-x_0⟩\end{array}$$
带Lagrange余项的泰勒公式

0阶：
$$f(x)=f(x_0)+⟨\nabla f(\xi ),x-x_0⟩$$
1阶：
$$f(x)=f(x_0)+⟨\nabla f(x_0),x-x_0⟩+\frac{1}{2}⟨{\nabla }^{2}f(\xi )(x-x_0),x-x_0⟩$$
带Peano余项的泰勒公式

0阶：
$$f(x)=f(x_0)+o(1)$$
1阶：
$$f(x)=f(x_0)+⟨\nabla f(x_0),x-x_0⟩+o(\Vert x-x_0\Vert )$$
2阶：
$$\begin{array}{c}f(x)=f(x_0)+⟨\nabla f(x_0),x-x_0⟩+\frac{1}{2}⟨{\nabla }^{2}f(x_0)(x-x_0),x-x_0⟩\\ +o(\Vert x-x_0{\Vert }^2)\end{array}$$
其中，$⟨x,y⟩$表示 $x$ 和 $y$ 的内积（i.e. 若$x,y\in {\mathbb{R}}^d$，则 $⟨x,y⟩=x^{T}y$）；$\Vert x\Vert$ 表示 $x$ 的范数，$\Vert x\Vert =\sqrt{⟨x,x⟩}$。

简单粗暴地推导Taylor公式的各种形式 - 知乎 (zhihu.com)

2.2 基本 ELQ

首先，定义本文中量化函数的形式为：
Q l = { α l c k ∣ 1 ≤ k ≤ K } {Q_{l}}=\{\alpha_{l}c_{k}|{1}\leq k\leq K\} Ql​={αl​ck​∣1≤k≤K}其中，$L$表示量化中心的总个数；${\alpha }_l$ 表示按层收缩因子；$c_k$ 表示一个正整数。例如，二元量化中， K = 2 , c k ∈ { − 1 , + 1 } K=2,c_k\in\{-1,+1\} K=2,ck​∈{−1,+1}；三元量化中， K = 3 , c k ∈ { − 1 , 0 , + 1 } K=3,c_k\in\{-1,0,+1\} K=3,ck​∈{−1,0,+1}。

然后，为了联合考虑“近似误差”和“损失扰动”的影响，ELQ算法中重新定义了优化问题，即：
min ⁡ W l ^ L ( W l ) + a 1 L p ( W l , W l ^ ) + a 2 E ( W l , W l ^ ) s.t. W l ^ ∈ { α l c k ∣ 1 ≤ k ≤ K } , 1 ≤ l ≤ L \begin{array}{ll}\min_{\widehat{W_l}}&L(W_l)+a_1L_p(W_l,\widehat{W_l})+a_2E(W_l,\widehat{W_l})\\\\\text{s.t.}&\widehat{W_l}\in\{\alpha_lc_k|1\le k\le K\},1\le l\le L\end{array} minWl​ ​​s.t.​L(Wl​)+a1​Lp​(Wl​,Wl​ ​)+a2​E(Wl​,Wl​ ​)Wl​ ​∈{αl​ck​∣1≤k≤K},1≤l≤L​其中，$L$ 表示全精度模型的损失函数；$L_p$ 表示全精度模型和量化模型损失的差异；$E$ 表示全精度模型和量化模型的近似差异；$a_1,a_2\in {\mathbb{R}}^{+}$ 表示两个正则化系数。特别的，定义函数 $L_p,E$ 如下：
$$\begin{array}{rl}{L}_p(W_l,\widehat{W_l})& =|L(W_l)-L(\widehat{W_l})|\stackrel{(a)}{=}|\frac{\partial L}{\partial (W_l)}|\delta ,\\ E(W_l,\widehat{W_l})& =||W_l-\widehat{W_l}|{|}^2.\end{array}$$其中，等式 $\stackrel{(a)}{=}$ 成立是由于：对函数 $L_p$ 在 $W_l$ 处进行1阶Taylor展开，得到：
$$\begin{array}{rl}{L}_p(W_l,{\hat{W}}_l)& =|L(W_l)-L(W_l)-\frac{\partial L}{\partial (W_l)}(\widehat{W_l}-W_l)|\\ & =|\frac{\partial L}{\partial (W_l)}(W_l-\widehat{W_l})|\\ & =|\frac{\partial L}{\partial (W_l)}|\delta ,\end{array}$$其中，$\delta =|W_l-\widehat{W_l}|$。

为了简单起见，本文中假设一个线性关系 $\frac{\partial L}{\partial (W_l)}\propto \delta$。因此，得到全精度模型的更新规则是：
$$\begin{array}{r}{W}_l^t=W_l^{t-1}-\gamma \frac{\partial L}{\partial (W_l^{t-1})}-\lambda sign(W_l^{t-1}-{\widehat{W_l}}^{t-1}),\end{array}$$

最后，定义量化函数 $Q_l$ 中的收缩因子 ${\alpha }_l$ 为：
$${\alpha }_l=mean(W_l)+\beta max(W_l),$$其中，$\beta =0.05$表示超参，根据实验所得。那么可以定义二元/三元量化函数为：
$$\begin{array}{cc}\widehat{W_l}=\{\begin{array}{ll}{\alpha }_l& \text{if}{W}_l\ge 0\\ -{\alpha }_l& \text{otherwise},\end{array}& \widehat{W_l}=\{\begin{array}{ll}{\alpha }_l& \text{if}{W}_l>0.5{\alpha }_l\\ -{\alpha }_l& \text{if}{W}_l<-0.5{\alpha }_l\\ 0& \text{otherwise}.\end{array}\end{array}$$
注：本文没有介绍阈值$\Delta$的介绍，只是定义 $\Delta =0$或者$\Delta =\pm 0.5{\alpha }_l$。

2.3 ELQ和增量策略的结合

仿照 “一” 中的思想，本文采取逐步量化的策略，即分为 “模型分类、模型量化、重训练” 三个步骤。那么全精度模型的更新规则修改为：
$$W_l^t=W_l^{t-1}-\gamma \frac{\partial L}{\partial (W_l^{t-1})}\odot T_l-\lambda sign(W_l^{t-1}-{\widehat{W_l}}^{t-1})\odot T_l$$其中，矩阵$T_l$定义为：
$$\begin{array}{cc}{T}_l=\{\begin{array}{ll}0& \text{if }{W}_l\odot T_l\in W_a,\\ 1& \text{if }{W}_l\odot T_l\in W_b,\end{array}& W_a\cup W_b=W_l\mathrm{and}{W}_a\cap W_b=\varnothing .\end{array}$$

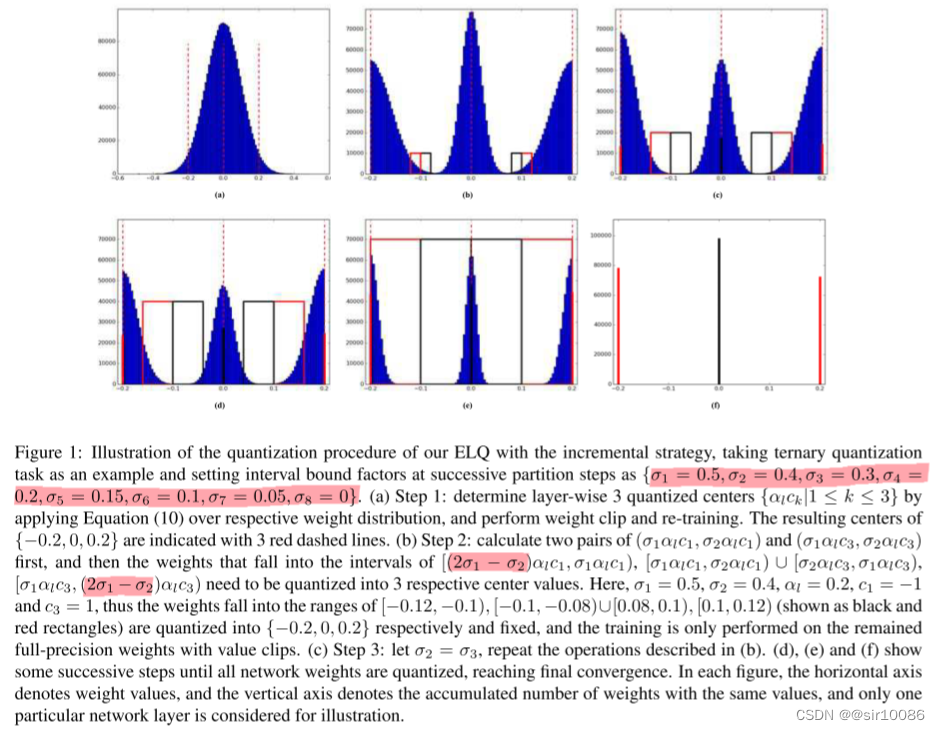
与 “一” 中的不同点在于 “模型量化” 上。其核心思想是：当权重的训练越靠近量化权重中心时（例如对于三元量化，有3个量化权重中心，$-\alpha ,0,+\alpha$），将更加有利于重训练过程；因此，本文将远离量化权重中心的值量化为中心点，然后进行重训练。这会带来一个问题：如何判断哪些值时远离量化权重中心的呢？本文定义了interval bound factor { σ n ∈ [ 0 , 1 ] ∣ 1 ≤ n ≤ N } \{\sigma_{n}\in[0,1]|1\leq n\leq N\} {σn​∈[0,1]∣1≤n≤N}来进行确定。另外，本文根据经验对三元量化选择 { σ 1 = 0.5 , σ 2 = 0.4 , σ 3 = 0.3 , σ 4 = 0.2 , σ 5 = 0.15 , σ 6 = 0.1 , σ 7 = 0.05 , σ 8 = 0 } \{\sigma_{1}=0.5,\sigma_{2}=0.4,\sigma_{3}=0.3,\sigma_{4}=0.2,\sigma_5=0.15,\sigma_6=0.1,\sigma_7=0.05,\sigma_8=0\} {σ1​=0.5,σ2​=0.4,σ3​=0.3,σ4​=0.2,σ5​=0.15,σ6​=0.1,σ7​=0.05,σ8​=0}，文中给出一个示例：

综上，得出ELQ算法流程为：

3. 讨论

本文主要创新点如下：

• 通过综合考虑之前成果中的 近似误差和损失扰动，来重写损失函数，以增加量化后模型的测试精度
• 模仿 “一” 中的增量量化策略，但修改了分组策略：将远离权重中心点的值最为量化的一组，其余的作为固定的一组，然后精心重训练

缺点如下：

• 没有详细解释量化函数中的阈值 $\Delta$，而是直接定义 $\Delta =0$或者$\Delta =\pm 0.5{\alpha }_l$
• 对新提出的分组策略没有详尽地介绍，即如何得到interval bound factor $\sigma$ 的取值

三、RPR: Random partition relaxation for training; Binary and ternary weight neural networks

Cavigelli L, Benini L. RPR: Random partition relaxation for training; Binary and ternary weight neural networks[J]. arXiv preprint arXiv:2001.01091, 2020.
arXiv 2020

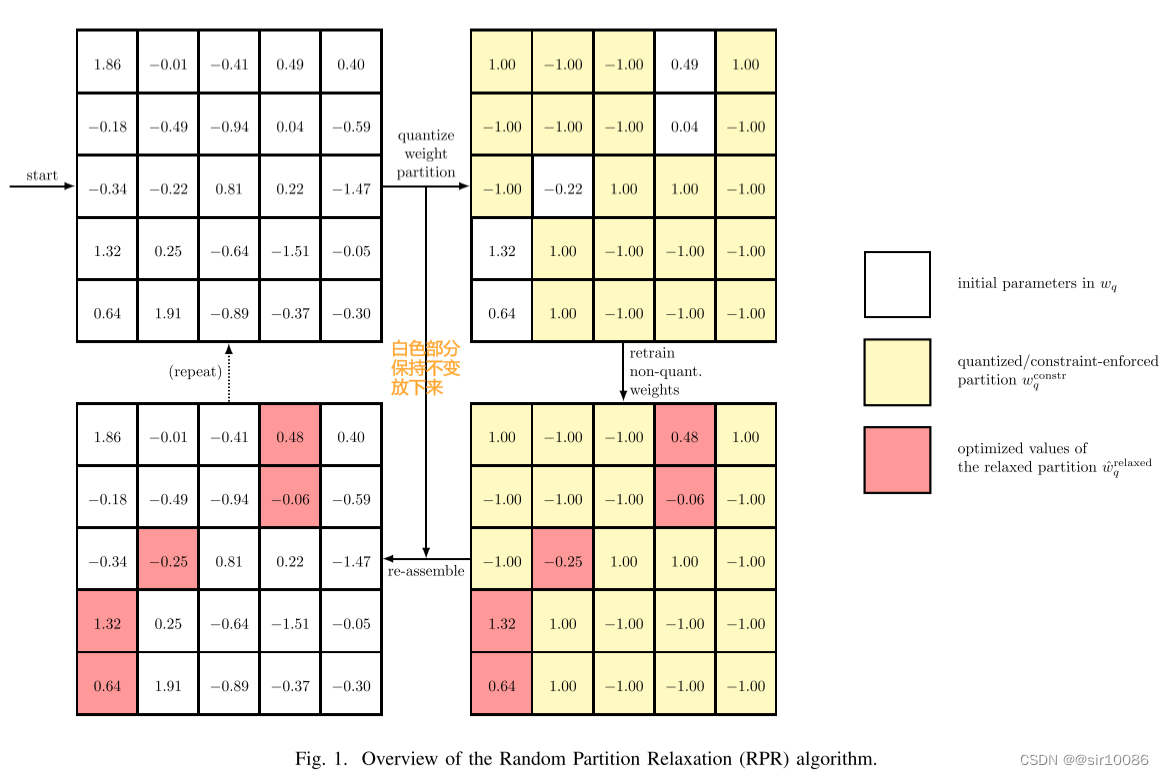
本文中心思想为：将待量化的权重 ${\mathbb{W}}_q$ 按照 冻结因子$FF=\frac{{\mathbb{W}}_q^{constr}}{{\mathbb{W}}_q}\in [0,1]$ 随机分为 ${\mathbb{W}}_q^{constr}$ 和 ${\mathbb{W}}_q^{relaxed}$。首先，选择一个 $FF$ 的值，将 ${\mathbb{W}}_q^{constr}$ 中的权重量化，然后重训练修改 ${\mathbb{W}}_q^{relaxed}$，最后重新将为量化之前的 ${\mathbb{W}}_q^{constr}$ 值代入。重复上述过程，直到 $FF=1$ 时模型依旧可以收敛，量化后的结果就是最终结果。一个简单的示例如下：

四、Two-Step Quantization for Low-bit Neural Networks

Wang P, Hu Q, Zhang Y, et al. Two-step quantization for low-bit neural networks[C]//Proceedings of the IEEE Conference on computer vision and pattern recognition. 2018: 4376-4384.
CVPR 2018 CCF-A会

1. 动机和贡献

动机： DNN的量化过程中，需要量化两种参数：“权重”和“激活”，但是当这两种参数同时使用较低精度量化时，模型测试精度下降会十分严重，甚至导致模型不能收敛。
注：和之前不同的是，本文提到了量化“激活”。具体概念在 2.1 中解释。

贡献： 为了解决同时量化 “权重”和“激活” 导致的模型性能下降的问题，本文提出了一种 两步走量化策略TSQ，来解耦权重量化过程和激活量化过程，主要包括如下两个部分：

1. code learning（量化激活）：利用网络中的 “激活稀疏性activation sparsity” 进行量化；
   注：大多文献关注权重的稀疏性，而没有解决激活的稀疏性
2. transformation function learning（量化权重）：当激活量化之后，认为它已经是最忧，然后利用 “最小二乘法” 优化权重。

2. 算法

2.1 量化权重与量化激活

传统DNN的优化问题可以转化为量化后DNN的优化问题，具体表示为：
minimize L ( Z L , y ) subject to Z l = W l A l − 1 A l = ψ ( Z l ) , for l = 1 , 2 , ⋯ L ⇒ t a n s l a t e   i n t o minimize ⁡ { W l } L ( Z L , y ) subject to  W ^ l = Q w ( W l )    Z l = W ^ l A ^ l − 1    A l = ψ ( Z l )    A ^ l = Q a ( A l ) , f o r l = 1 , 2 , ⋯ L \begin{array}{ll}\text{minimize}&\mathcal{L}(Z_L,y)\\\text{subject to}&Z_l=W_lA_{l-1}\\&A_l=\psi(Z_l),\text{for}l=1,2,\cdots L\end{array} \overset{tanslate~into}{\Rightarrow}\quad \begin{aligned} &\operatorname*{minimize}_{\{W_{l}\}} \mathcal{L}(Z_{L},y) \\ &\text{subject to}~ \hat{W}_{l}=Q_{\boldsymbol{w}}(W_{l}) \\ &\qquad\qquad~~ Z_{l}=\hat{W}_{l}\hat{A}_{l-1} \\ &\qquad\qquad~~ A_{l}=\psi(Z_{l}) \\ &\qquad\qquad~~ \hat{A}_{l}={Q}_{\boldsymbol{a}}(A_{l}),\mathrm{for}l=1,2,\cdots L \end{aligned} minimizesubject to​L(ZL​,y)Zl​=Wl​Al−1​Al​=ψ(Zl​),forl=1,2,⋯L​⇒tanslate into​{Wl​}minimize​L(ZL​,y)subject to W^l​=Qw​(Wl​)  Zl​=W^l​A^l−1​  Al​=ψ(Zl​)  A^l​=Qa​(Al​),forl=1,2,⋯L​其中，$W_l$ 表示第 $l$ 层权重，$Q_{\mathbf{w}}\psi (\cdot )$ 表示权重量化函数；$A_l$ 表示第 $l$ 层激活（$A_0$就是输入数据），$Q_{\mathbf{a}}$ 表示激活量化函数；$\psi (\cdot )$ 表示DNN中的激活函数。

2.2 Code Learning（量化激活）

在这个阶段，所有的权重都是全精度的，只有激活会被量化，其核心思想是：绝对值大的激活对网络的左右大于小的，因此，引入稀疏度将所有低于某个阈值的激活设置为 $0$，用数学语言定义为：给定一个稀疏阈值（sparse threshold） $ϵ$，那么量化函数为：
$$Q_{ϵ}(x)=\{\begin{array}{cl}{q}_i^{\prime }& x\in (t_i^{\prime },t_{i+1}^{\prime }],\\ 0& x\le ϵ,\end{array}$$那么，量化函数可以由解决以下优化问题得到：
$$Q_{ϵ}^{\ast }(x)=\underset{Q_{ϵ}}{\mathrm{argmin}}{E}_{x\sim \mathcal{N}(0,1),x>ϵ}[(Q_{ϵ}(x)-x{)}^2],$$最后，稀疏阈值 $ϵ$定义为：经过 批归一化batch normalization，每层的输出近似为一个标准正太分布 $x\sim \mathcal{N}(0,1)$，因此，给定一个稀疏度 $\theta$，稀疏阈值通过解决如下等式得到：
$$\Phi (ϵ)=P(x<=ϵ)=\theta .$$

注：上述过程说明，只要获得了稀疏度 $\theta$ 就可以得到量化函数。那么，如何获得稀疏度 $\theta$ 呢？本文没有详细说明，我认为是通过预处理过程吗？

2.3 Transformation Function Learning（量化权重）

经过 Code Learning，认为激活的量化已经是最优，表示为 ${\hat{A}}_l$。这个阶段，主要是考虑如何学习 ${\hat{A}}_{l-1}\to {\hat{A}}_l$ 的转换函数。假设 ${\hat{A}}_{l-1},{\hat{A}}_l$ 表示为 $X,Y$，那么，转换函数学习问题的解决如同解决如下最小二乘问题：
minimize ∥ Y − Q ϵ ( Λ W ^ X ) ∥ F 2 = minimize ∑ { α i } , { w ^ i T } ∥ y i T − Q ϵ ( α i w ^ i T X ) ∥ 2 2 \begin{aligned}&\text{minimize}\quad\parallel Y-Q_\epsilon(\Lambda\hat{W}X)\parallel_F^2\\=&\text{minimize}\quad\sum_{\{\alpha_i\},\{\hat{w}_i^T\}}\parallel y_i^T-Q_\epsilon(\alpha_i\hat{w}_i^TX)\parallel_2^2\end{aligned} =​minimize∥Y−Qϵ​(ΛW^X)∥F2​minimize{αi​},{w^iT​}∑​∥yiT​−Qϵ​(αi​w^iT​X)∥22​​其中，${\alpha }_i$ 表示量化后权重 ${\hat{w}}_i$ 的全精度缩放因子。
注：本文中 ${\alpha }_i$ 表示为量化后卷积核 ${\hat{w}}_i$ 的全精度缩放因子。

由于量化函数 $Q_{ϵ}(\cdot )$ 没办法求导，因此本文中，通过引入一个辅助变量 $z$ 来解决，即：
$$\underset{\alpha .\hat{w}}{\mathrm{minimize}}\parallel y-Q_{ϵ}(\alpha X^T\hat{w}){\parallel }_2^2\Rightarrow \underset{\alpha ,\hat{w},z}{\mathrm{minimize}}\parallel y-Q_{ϵ}(z){\parallel }_2^2+\lambda \parallel z-\alpha X^T\hat{w}{\parallel }_2^2$$其中，$\lambda$ 表示惩罚系数。

为了解决上述问题，本文采取交替策略，即：

1. 固定 $z$，优化 $\alpha ,\hat{w}$：优化问题转化为
   $$\underset{\alpha ,\hat{w}}{\mathrm{minimize}}J(\alpha ,\hat{w})=\parallel z-\alpha X^T\hat{w}{\parallel }_2^2$$通过设置 $\partial J/\partial \alpha =0$，得到
   $${\alpha }^{\ast }=\frac{z^T{X}^T\hat{w}}{{\hat{w}}^{T}X{X}^T\hat{w}}\stackrel{代入原式}{\Rightarrow }{\hat{w}}^{\ast }=\underset{\hat{w}}{\mathrm{argmax}}\frac{(z^T{X}^T\hat{w}{)}^2}{{\hat{w}}^{T}X{X}^T\hat{w}}$$这样，就可以通过 ”暴力搜索“ 的方式，得到最佳的 $\alpha ,\hat{w}$。
2. 固定 $\alpha ,\hat{w}$，优化 $z$：优化问题转化为
   $$\underset{z_i}{\min }\text{minimize}(y_i-Q_{ϵ}(z_i){)}^2+\lambda (z_i-v_i{)}^2,$$其中，$v=\alpha X^T\hat{w}$是一个已知向量。为了进一步简化问题，将量化函数 $Q_{ϵ}$ 放缩为 ${\tilde{Q}}_{ϵ}$:
   $${\tilde{Q}}_{ϵ}(x)=\{\begin{array}{cl}M& x>M,\\ x& 0<x\le M,\\ 0& x\le 0.\end{array}$$那么，上述优化问题可以通过分类讨论得到解：
   $$\{\begin{array}{ll}{z}_i\le 0& \Rightarrow z_i^{(0)}=min(0,v_i)\\ 0<z_i\le M& \Rightarrow z_i^{(1)}=min(M,max(0,\frac{\lambda v_i+y_i}{1+\lambda })\\ M<z_i& \Rightarrow z_i^{(2)}=max(M,v_i)\end{array}$$

关于初始化 $\alpha ,\hat{w}$ 的方式：本文通过解决如下优化问题，获得初始化值：
minimize ∥ w − α w ^ ∥ 2 2 subject to α > 0 w ^ ∈ { − 1 , 0 , + 1 } m , \begin{array}{ll}\text{minimize}&\parallel w-\alpha\hat{w}\parallel_2^2\\\text{subject to}&\alpha>0\\&\hat{w}\in\{-1,0,+1\}^m\end{array}, minimizesubject to​∥w−αw^∥22​α>0w^∈{−1,0,+1}m​,那么，
$$\begin{array}{rl}{\alpha }^{\ast }& =\frac{w^T\hat{w}}{{\hat{w}}^T\hat{w}}\\ {\hat{w}}^{\ast }& =\underset{\hat{w}}{\mathrm{argmax}}\frac{(w^T\hat{w}{)}^2}{{\hat{w}}^T\hat{w}}\end{array}.$$

3. 讨论

本文主要贡献是

• 通过 ”两步走“ 的策略，当 权重量化和激活量化解耦
• 本文量化第 $l$ 层时，前 $l-1$ 层已经量化完毕，表示为
  $$\underset{\Lambda ,\hat{W}}{\mathrm{minimize}}\parallel Y-Q_{ϵ}(\Lambda \hat{W}\tilde{X}){\parallel }_F^2$$这就解决了不同层独立量化中出现的 误差积累 的问题

借鉴点：

• 对不同层之间的量化方式可以不是独立，这样可以缓解误差的积累问题
• 之前都是考虑量化权重，是否可以考虑量化激活

五、Ternary Neural Networks with Fine-Grained Quantization

Mellempudi N, Kundu A, Mudigere D, et al. Ternary neural networks with fine-grained quantization[J]. arXiv preprint arXiv:1705.01462, 2017.
arXiv 2017

1. 动机和贡献

动机： 低精度模型可以减少计算量和内存消耗，对边缘设备是十分友好的，但是却面临着测试精度下降的问题。

贡献： 本文提出一种细粒度的量化策略FGQ，在没有重训练的情况下，使用三元表示梯度，取得了较好的测试精度。

2. 算法

2.1 问题引出

TWN 中三元量化可以表示为：
α ∗ , Δ ∗ = argmin ⁡ α ≥ 0 , Δ > 0 E ( α , Δ ) = d e f ∥ W − α W ^ ∥ F 2 , s . t .   α ≥ 0 , W ^ i ∈ { − 1 , 0 , + 1 } , i = 1 , 2 , ⋯   , n \alpha^{*},\Delta^{*}=\underset{\alpha\geq0,\Delta>0}{\operatorname*{argmin}}E(\alpha,\Delta)\overset{def}{=}\|\mathbf{W}-\alpha\hat{\mathbf{W}}\|_F^2,\\\mathrm{s.t.}~\alpha\geq0,\hat{\mathbf{W}}_{i}\in\{-1,0,+1\},i=1,2,\cdots,n α∗,Δ∗=α≥0,Δ>0argmin​E(α,Δ)=def∥W−αW^∥F2​,s.t. α≥0,W^i​∈{−1,0,+1},i=1,2,⋯,n其中，$W\in {\mathbb{R}}^n$；同时，为了更好地表示正负权重的不同分布，通常也会对其使用不同的阈值参数 ${\Delta }_p\text{ and }{\Delta }_n>0$。但是使用单一或者少数的阈值 $\Delta$ 和 缩放因子 $\alpha$ 会导致量化后权重不能很好表示原始权重之间不同的分布，从而导致量化误差的增大。

基于此，本文提出了一种新的更细粒度的算法。

2.2 算法描述

假设 $I$ 表示权重 $W\in {\mathbb{R}}^n$ 的 $n$ 个索引组成的集合。将 $I$ 正交的分为 $k$ 个子集，表示为 $c_1,c_2\cdots c_k$，则有 $c_i\cap c_j=\varnothing ,{\cup }_i{c}_i=I,{\sum }_i{n}_i=n$。同理，权重 $W$ 也分为 $k$ 个正交向量 $W^{(i)}\in {\mathbb{R}}^n,i=1,2,\cdots ,k$，且 ${\mathbf{W}}_j^{(i)}={\mathbf{W}}_j\text{ if }j\in c_i,\text{ otherwise }0$，因此有 ${\sum }_i{\mathbf{W}}^{(i)}=\mathbf{W}$。根据其正交性，可以有：
$$({\mathbf{W}}^{(i)}-{\alpha }_i{\hat{\mathbf{W}}}^{(i)})\perp ({\mathbf{W}}^{(j)}-{\alpha }_j{\hat{\mathbf{W}}}^{(j)}),\mathrm{for}i\ne j\Rightarrow \Vert \mathbf{W}-\sum _i{\alpha }_i{\hat{\mathbf{W}}}^{(i)}{\Vert }_F^2=\sum _i\Vert {\mathbf{W}}^{(i)}-{\alpha }_i{\hat{\mathbf{W}}}^{(i)}{\Vert }_F^2$$那么上述优化问题转换为：
$${\alpha }_1^{\ast },..,{\alpha }_k^{\ast },{\hat{\mathbf{W}}}^{(1)\ast },..,{\hat{\mathbf{W}}}^{(k)\ast }=\underset{{\alpha }_i,{\hat{\mathbf{W}}}^{(i)}}{\mathrm{argmin}}\Vert \mathbf{W}-\sum _i{\alpha }_i{\hat{\mathbf{W}}}^{(i)}{\Vert }_F^2=\sum _i\underset{{\alpha }_i,{\hat{\mathbf{W}}}^{(i)}}{\mathrm{argmin}}\Vert {\mathbf{W}}^{(i)}-{\alpha }_i{\hat{\mathbf{W}}}^{(i)}{\Vert }_F^2$$这样，就可以单独解决 $k$ 个子问题。

另外，如果对正负权重使用不同的阈值，则优化问题是：
α ∗ , Δ p ∗ , Δ n ∗ = argmin ⁡ α ≥ 0. Δ n > 0. Δ n > 0 ∥ W − α W ^ ∥ F 2 , s . t . W ^ i ∈ { − 1 , 0 , + 1 } , i = 1 , ⋯   , n . \alpha^{*},\Delta_{p}^{*},\Delta_{n}^{*}=\underset{\alpha\geq0.\Delta_{n}>0.\Delta_{n}>0}{\operatorname*{argmin}}\|\mathbf{W}-\alpha\hat{\mathbf{W}}\|_{F}^{2},\quad\mathrm{s.t.}\quad\hat{\mathbf{W}}_{i}\in\{-1,0,+1\},i=1,\cdots,n. α∗,Δp∗​,Δn∗​=α≥0.Δn​>0.Δn​>0argmin​∥W−αW^∥F2​,s.t.W^i​∈{−1,0,+1},i=1,⋯,n.

根据 TWN 中给出的解析解，有：
$${\alpha }^{\ast }=(\sum _{i\in I_{\Delta }}|{\mathbf{W}}_i|)/|I_{\Delta }|,{\Delta }^{\ast }={\mathrm{argmax}}_{\Delta >0}(\sum _{i\in I_{\Delta }}|{\mathbf{W}}_i|{)}^2/|I_{\Delta }|$$或者
$${\Delta }_p^{\ast },{\Delta }_n^{\ast }={\mathrm{argmax}}_{{\Delta }_p>0,{\Delta }_n>0}\frac{({\sum }_{i\in I_{\Delta }^{+}}|{\mathbf{W}}_i|+{\sum }_{i\in I_{\Delta }^{-}}|{\mathbf{W}}_i|{)}^2}{|I_{\Delta }^{+}|+|I_{\Delta }^{-}|},{\alpha }^{\ast }=\frac{{\sum }_{i\in I_{\Delta }^{+}}|{\mathbf{W}}_i|+{\sum }_{i\in I_{\Delta }^{-}}|{\mathbf{W}}_i|}{|I_{\Delta }^{+}|+|I_{\Delta }^{-}|}$$

那么，如何进行分组？
原文中没有详细给出分组策略，只是给出分组需要遵守的原则是：尽可能使组中权重有着相同的数据分布。
原文中也提到了使用K-means聚类方法，只不过对算力有一定要求。

六、SYQ: Learning Symmetric Quantization For Efficient Deep Neural Networks

Faraone, Julian, et al. “Syq: Learning symmetric quantization for efficient deep neural networks.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018.
CVPR 2018 CCF-A会

1. 动机和贡献

动机： 由于量化导致DNN前馈和后馈过程中大量梯度的错配，因此导致推理过程中模型精度的大幅度下降。

贡献： 本文提出一种 “对称性三元量化”策略SYQ。首先通过权重的位置对其进行分组，然后对不同组权重给出不同的缩放因子。
注：本文中主要关心DNN中的 “卷积层CONV”。

2. 算法

2.1 权重量化

根据 TWN 中的描述，三元量化函数定义为：
$$Q_l=sign(W_l)\odot M_l,$$其中，权重 $W_l\in {\mathbb{R}}^{K\times K\times I\times N}$，$K$表示卷积核大小，$I$表示输出特征数，$N$表示输出特征数；掩码矩阵定义为：
$$M_{l_{i,j}}=\{\begin{array}{ll}1& \text{if}|W_{l_{i,j}}|\ge {\eta }_l\\ 0& \text{if}-{\eta }_l<W_{l_{i,j}}<{\eta }_l\end{array}$$根据 TTQ 中定义，阈值 $\eta =0.05\times \max (\Vert W_l\Vert )$。类似于TTQ中解决梯度消失的方式，本文中也采用STE的方式，即：
$$\frac{\partial \hat{E}}{\partial W_{l_{i,j}}}=\frac{\partial \hat{E}}{\partial Q_{l_{i,j}}},$$其中，$\hat{E}$ 表示没有缩放因子的误差函数

2.2 收缩因子定义和分组

收缩因子 $c_i$ 采用和TWN中相同的对称收缩因子的定义方式，本文采用的数学语言描述为：
$$\forall c_i\in C^p,\exists |c_j|\in C^n\text{where}{c}_i=|c_j|,$$其中， C p = { c i ∣ c i > 0 } , C n = { c j ∣ c j < 0 } C^{p}=\{c_{i}|c_{i}>0\},C^n=\begin{Bmatrix}c_j|c_j<0\end{Bmatrix} Cp={ci​∣ci​>0},Cn={cj​∣cj​<0​}。因此，使用STE方法有：
$$\frac{\partial E}{\partial W_{l_{i,j}}}=\frac{\partial E}{\partial Q_{l_{i,j}}}={\alpha }_l^i\frac{\partial \hat{E}}{\partial Q_{l_{i,j}}}.$$
因此，本文可以采用和TWN、TTQ相同的思路，采用向后传播的方式逐步更新缩放因子，其初始值定义为相对应权重绝对值的均值，即：
$${\alpha }_{l_0}^i=\frac{{\sum }_{j\in S_l^i}\left|{\tilde{W}}_{l_{i,j}}\right|}{I\times N}.$$

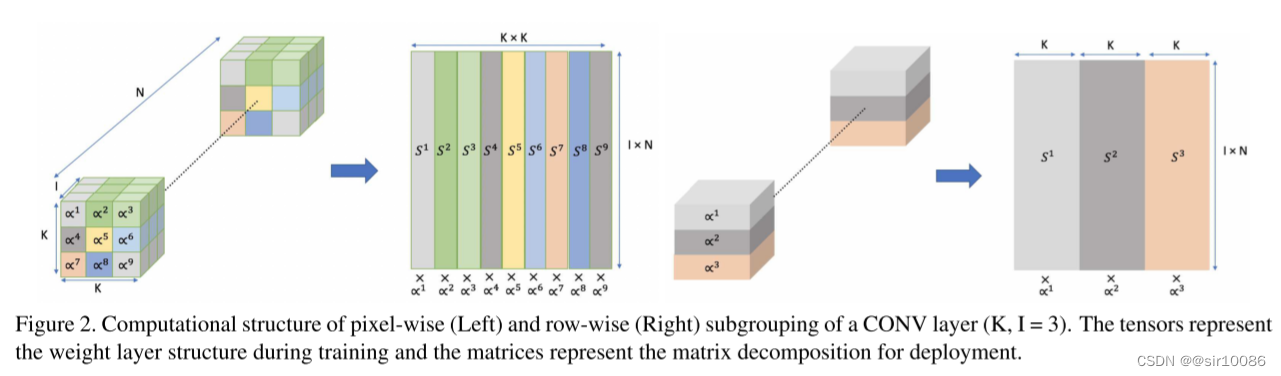
分组方式： 本文中的分组方式是一个比较新颖的点，包括两种方式，c。但是对于这两种方式的具体优势，本文没有给出。下图是这种分组方式的示意图：

3. 讨论

本文基本采用TWN、TTQ这两篇文章的中心思想，有所不同的是给出两种权重分组策略，所以我认为创新性不太充足。

缺点：

• 本文中对误差函数的定义没有详细说明，可能采用与TWN、TTQ中相同的定义方式，即$J(\alpha ,\hat{W}=\Vert W-\alpha \hat{W}{\Vert }_2^2)$；
• 对收缩因子的定义不清，似乎本文收缩因子绝对值采用 “绝对值权重和的平均” 来定义；
• 对于文中所提到的pixel-wise和row-wise的两种分组方式，都是适用于卷积层CONV，对于其他类型的学习算法，并不适用。

七、Fixed-point factorized networks

Wang P, Cheng J. Fixed-point factorized networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 4012-4020.
CVPR 2017 CCF-A会

1. 动机和贡献

动机： 为了压缩DNN模型，并加快其训练过程，同时尽可能地减少推理精度损失。

贡献： 本文提出了一种基于矩阵不动点分解网络模型 FFN，将原始全精度权重使用 $(-1,0,+1)$ 三元组表示，具体分为如下三个部分：

• direct fixed-point factorization：基于矩阵不动点分解，FFN分解原始全精度权重，这种分解方式十分灵活且准确；
• full precision weight recovery：进行梯度累加时，如果直接使用量化值进行相加，会损失重要信息，因此，本文将量化值重新恢复为（伪）全精度值进行梯度累加；
• weight balancing：由于分解形式不是唯一的，使用分解技术通常会产生权重不平衡问题，因此，本文提出了一种有效的权重平衡策略。

2. 算法

2.1 Fixed-point Factorization of Weight Matrices

假设全精度权重矩阵为 $W\in R^{m\times n}$，那么其半离散分解SDD可以表示为：
minimize ⁡ X , D , Y ∥ W − X D Y T ∥ F 2 = minimize ⁡ { x i } , { d i } , { y i } ∥ W − ∑ i k d i x i y i T ∥ F 2 \begin{equation*} \begin{split} &\qquad\underset{{X,D,Y}}{\operatorname{minimize}}\parallel W-XDY^T\parallel_F^2\\\\&=\underset{{\{x_i\},\{d_i\},\{y_i\}}}{\operatorname{minimize}}\parallel W-\sum_i^kd_ix_iy_i^T\parallel_F^2 \end{split} \end{equation*} ​X,D,Yminimize​∥W−XDYT∥F2​={xi​},{di​},{yi​}minimize​∥W−i∑k​di​xi​yiT​∥F2​​​其中， X ∈ { − 1 , 0 , + 1 } m × k , Y ∈ { − 1 , 0 , + 1 } n × k X\in\{-1,0,+1\}^{m\times k},Y\in\{-1,0,+1\}^{n\times k} X∈{−1,0,+1}m×k,Y∈{−1,0,+1}n×k，$D\in R_{+}^{k\times k}$ 是一个对角矩阵，$k$ 代表了SDD分解的维数（选择不同的$k$可以尽可能准确的模拟原始全精度权重，注意到$k$可以比$m,n$都要大）。

由于上述优化问题的三元值限制，这是一个NP问题，本文借用[19]中的内容，使用贪心策略得到其近似解，具体过程见如下算法：

2.2 Full-precision Weight Recovery

假设 $X,Y$ 的全精度表示为 $\hat{X},\hat{Y}$，注意到 $\hat{X},\hat{Y}$ 必须量化到 $X,Y$。本文中，将全精度权重恢复技术视为量化过程的逆过程，描述为：
$$\begin{array}{rl}\mathrm{minimize}& \parallel W-\hat{X}D{\hat{Y}}^T{\parallel }_F^2\\ \mathrm{subject}\mathrm{to}& \mid {\hat{X}}_{ij}-X_{ij}\mid <0.5,\forall i,j\\ & \mid {\hat{Y}}_{ij}-Y_{ij}\mid <0.5,\forall i,j\end{array}$$这里的两个限制条件是为了 $\hat{X},\hat{Y}$ 可以量化到 $X,Y$。注意到 $\hat{X},\hat{Y}\in [-1.5,1.5]$，同时一开始原始权重也限制到 $[-1.5,1.5]$ 之内。因此，$\hat{X},\hat{Y}$ 的量化可以是：
$$q(A_{ij})=\{\begin{array}{cc}+1& 0.5<A_{ij}<1.5\\ 0& -0.5\le A_{ij}\le 0.5\\ -1& -1.5<A_{ij}<-0.5\end{array}$$

2.3 Weight Balancing

这是由于 “矩阵的不动点分解不存在唯一的分解形式” 所导致的问题。由于不是本阶段关注重点，所以此部分略过。

3. 讨论

和传统量化方式不同，本文利用 矩阵的不动点分解进行量化，使得量化过程更加灵活、准确。

可参考的点儿：

• 在梯度累加时使用（伪）全重精度权重，可以降低损失；
• 由于（伪）全精度权重恢复的需要，原始权重可以归一到区间 $[-1.5,1.5]$，而不是传统意义上的 $[-1.1]$；