计算几何：凸包

极点：在一组点中，若沿着某一个点做直线，必然能找到一条直线使得所有点都在直线的另一侧，则这个点为极点。

凸包：给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点

 

平面的一个子集S被称为是“凸”的，当且仅当对于任意两点p，s∈S，线段ps都完全属于S。（平面凸包定义）：

计算凸包：

Graham扫描法: 复杂度O(nlogn) 

求得凸包中的点是按逆时针排序的

<=表示如果存在共线的极点，则只取端点

扫描方法有两种，可以用极角序（按极角排序）或坐标序（按x坐标排序，x坐标一样按y坐标排序，其中扫描上凸包是从大到小，扫描下凸包是从小到大）

1. 找到最左下的点(即y最小，y一样取最左边的)，赋给p[1]
2. 以p[1]作为极点，将所有点按极角排序，极角相同则按距离排序（去掉极角相同的，只留下距离最远的那个点）
3. 求凸包时while循环把发现不是凸包顶点的点移除出去。因为当逆时针遍历凸包时，我们应该在每个顶点向左转，因此当while循环发现在一个顶点处没有向左转时，就把该顶点移除出去。

计算凸包周长：

hdu1392:Surround the Trees

//以左下点为极点求凸包周长

#include<bits/stdc++.h>
using namespace std;

struct point{
    double x,y;
    point friend operator -(point a,point b)
    {return {a.x-b.x,a.y-b.y};}
}p[105],s[105];//p为所有点的集合,s为凸包点集
double dis(point a,point b)
{
    point c=a-b;
    return sqrt(c.x*c.x+c.y*c.y);
}
double cross(point a,point b)
{
    return a.x*b.y-a.y*b.x;
}
//按照极角(polar angle)从小到大排序(以 p1为极点)
//极角相同的点按照到的距离从小到大排序。
int cmp(point a,point b)
{
    double x=cross(a-p[1],b-p[1]);

    if(x>0) return 1;
    if(x==0&&dis(a,p[1])<dis(b,p[1])) return 1;
    return 0;
}
double multi(point p1,point p2,point p3)//计算向量叉积
{
    return cross(p2-p1,p3-p1);
}
int main()
{
    int N;
    while(scanf("%d",&N),N)
    {
        for(int i=1;i<=N;i++) cin>>p[i].x>>p[i].y;

        if(N==1)
        {
            printf("0.00\n");
            continue;
        }
        else if(N==2)
        {
            printf("%.2lf\n",dis(p[1],p[2]));
            continue;
        }

        int k=1;
        for(int i=2;i<=N;i++)
        if(p[i].y<p[k].y||(p[i].y==p[k].y&&p[i].x<p[k].x))k=i;
        swap(p[1],p[k]);//找到处于最左下方的点,赋给p[1]

        sort(p+2,p+1+N,cmp);//对点按极角排序,p[1]为极点

        s[1]=p[1];
        s[2]=p[2];
        int cnt=2;
        //while循环把发现不是凸包顶点的点移除出去,因为当逆时针遍历凸包时，我们应该在每个顶点向左转
        //因此当while循环发现在一个顶点处没有向左转时，就把该顶点移除出去。
        for(int i=3;i<=N;i++)//求凸包
        {
            while(cnt>=2&&multi(s[cnt-1],s[cnt],p[i])<=0) cnt--;
            s[++cnt]=p[i];
        }
        double sum=0;
        for(int i=1;i<cnt;i++)//求凸包周长
            sum+=dis(s[i],s[i+1]);
        printf("%.2f\n",sum+dis(s[1],s[cnt]));
        /*
        double area=0;
        for(int i=2;i<=cnt-1;i++)//求凸包面积，这里因为就是凸多边形所以可以用某个顶点作为顶点分割三角形
            area+=fabs(multi(s[1],s[i],s[i+1]));
        printf("%d\n",int(area/100));
        */
        /*标准求多边形面积,别漏了最后一个和起点的叉积
        for(int i=1;i<=cnt;i++)//求凸包面积
            area+=cross(s[i],s[i==cnt?1:i+1]);
        if(area<0)
            area=-area;
        */
    }
    return 0;
}

分治法：求解上凸包和下图包合并

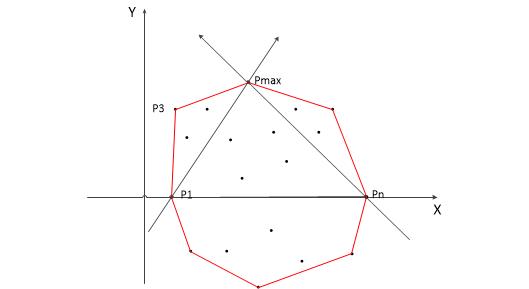
1. 按横坐标从小到大（再总坐标从小到大）排序，首先排序后的起终点必然在凸包里
2. 连接p1pn，这条直线将点集分成了上下两个部分，则在这两个部分中分别求得上、下凸包
3. 对于上凸包，找到上部分离直线最远的点pmax,连接p1max,pmaxpn，则直线p1pmax右将上部分分成了两个凸包部分
4. 重复，求下凸包类似
5. 判断点位于直线的左侧还是右侧可以用叉积

//这是三个点的叉乘（判断第三个点p3在直线p1p2的左方还是右方）左方>0
double multi(node p1, node p2, node p3)
{
	return p1.x*p2.y+p3.x*p1.y+p2.x*p3.y-p3.x*p2.y-p2.x*p1.y-p1.x*p3.y;
}

上凸包：即将点按x坐标从小到大排序，相当于以y轴负无穷处某一点为极点，从右往左扫描极点。这样算出来的凸包为上凸包。即在左右端点上方的极点

下凸包：即将点按x坐标从小到大排序，相当于以y轴负无穷处某一点为极点，从左往右扫描极点。这样算出来的凸包为上凸包。即在左右端点上方的极点

poj1113:Wall

theme:求能围住所有的点且距离所有点的距离>=L的围墙的长度

solution:即凸包周长+2*pi*L

//求能围住所有的点且距离所有点的距离>=L的围墙的长度

#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;

struct Point
{
	double x, y;

	Point operator-(Point & p)
	{
		Point t;
		t.x = x - p.x;
		t.y = y - p.y;
		return t;
	}

	double cross(Point p)
	{
		return x*p.y - p.x*y;
	}

	double dist(Point & p)
	{
		return sqrt((x - p.x)*(x - p.x) + (y - p.y)*(y - p.y));
	}
};

bool cmp(Point p1, Point p2)//先横坐标从小到大,再纵坐标从小到大
{
	if (p1.x != p2.x)
		return p1.x < p2.x;
	return p1.y < p2.y;
}

Point point[1005];
int convex[1005];
int N, L;

//返回极点个数+1
int getConvexHull()
{
	sort(point, point + N, cmp);
	int temp;
	int total = 0;
	for (int i = 0; i < N; i++)//求解下凸包,<=关系则如果存在共线的点只取端点
	{
		while (total > 1 && (point[convex[total - 1]] - point[convex[total - 2]]).cross(point[i] - point[convex[total - 1]]) <= 0)
			total--;
		convex[total++] = i;
	}
	//求解上凸包
	temp = total;
	for (int i = N - 2; i >= 0; i--)
	{
		while (total > temp && (point[convex[total - 1]] - point[convex[total - 2]]).cross(point[i] - point[convex[total - 1]]) <= 0)
			total--;
		convex[total++] = i;
	}
	return total;//返回组成凸包的点的个数，实际上多了一个,是起点(开始与最后都是起点),所以组成凸包的点个数是total-1
}

int main()
{
	scanf("%d%d", &N, &L);
	for (int i = 0; i < N; i++)
		scanf("%lf%lf", &point[i].x, &point[i].y);

	int num = getConvexHull();
	double ans = 0.0;
	for (int i = 0; i < num - 1; i++)
		ans += point[convex[i]].dist(point[convex[i + 1]]);
	ans += 3.14159265358927 * 2 * L;
	printf("%.0f\n", ans);
	return 0;
}
/*
9 100
200 400
300 400
300 300
400 300
400 400
500 400
500 200
350 200
200 200

1628
*/

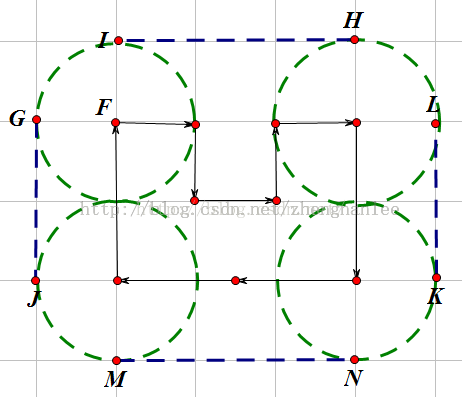
稳定凸包

即由这些点构成的凸多边形唯一，无论再添加多少新的点都不可能再形成别的凸多边形。

结论：稳定凸多边形的任意一条边的点数>=3

        

左边的凸包是不稳定的，因为加上一个点后可以形成一个新的凸多边形。

可以看出如果一个凸多边形的某一条边上只有端点两个点的话，则这个凸多边形是不稳定的。