飞行时间约束的弹道导弹轨迹仿真算法
关于弹道导弹轨迹仿真的研究思路及主要参考文献,可以参见博文《发射瞬时速度约束下的弹道导弹轨迹仿真算法》,本文不再赘述。本文主要是提出了另外一种弹道导弹轨迹仿真的算法。
一、STK中的固定飞行时间弹道导弹模型
STK中导弹对象的轨迹模型中的ballistic(弹道)有几种选项:Fixed Delta V、Fixed Delta V Min ECC、Fixed Apogee Alt、Fixed Time of Flight。
其中的Fixed Time of Flight模型界面如图所示。
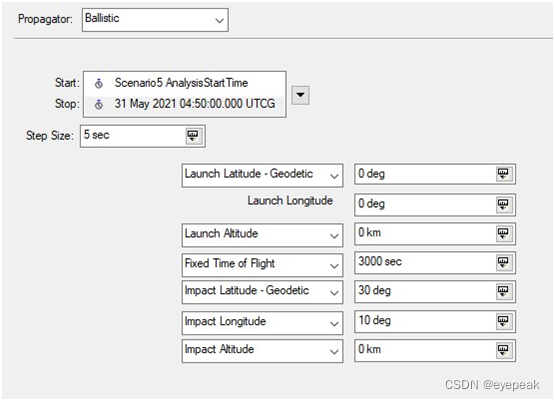
给定发射点和落点的经度、纬度和高度,以及飞行时间,根据二体模型计算导弹的轨迹。
其中的开始和结束时间,对于轨迹的形状没有影响。
当给定的飞行时间过短的时候,会出现提示对话框,并将发射点和落点所对应的最短时间填充在编辑框之内。
对于飞行时间上界,可以是非常大的数值,只有当极大极大的时候才会不支持。如发射点坐标为(0,0,0),落点(30,10,0),飞行时间10天,其计算得到的轨道半长轴为196187km,这显然没有实际的意义。注:以上坐标按经度、纬度、高度顺序,单位分别为°、°、km。
二、算法任务描述
本文拟实现的算法即类似于上述STK模型,即给定发射点、落点坐标(高度任意、不限于0km)、飞行时间,计算出对应的二体模型表示的导弹弹道。
可以看出,上述模型即为Lambert模型,相信STK中也是使用Lambert模型的。本文主要是想尝试利用搜索的方法来计算弹道。
在二体模型轨道的6个根数中,当确定了半长轴和偏心率之后,结合发射点和落点位置、地心的几何关系,可以很确定地计算出轨道倾角、升交点赤经、近地点幅角和平近点角,可参见博文《发射瞬时速度约束下的弹道导弹轨迹仿真算法》。
因此,现在要解决的算法归结为:给定轨道上2点,以及两点之间的飞行时间,计算出半长轴a和偏心率e。
三、已知条件的分析
用搜索的方法来找出答案,但显然不能穷举,而必须构造某种策略来进行搜索。那么,我们有哪些条件是可以利用的呢?
①给定飞行时间,意味着地球的自旋已知,因此可以直接确定经过该飞行时间的落点位置,即可以直接确定惯性坐标系下的落点位置,并基于此来计算半长轴和偏心率。
②轨道越高、飞行时间越长,因此,对于a,可以利用某些约束进行折半的搜索。
③给定a的情况下,需要对e进行搜索,以期找到符合某种条件的e值,同时其搜索结果应该可以指导a值的搜索方向。
④给定发射点和落点的位置,实际上就确定了两点之间的真近点角差。如图中的θ。该值可以利用余弦定理得到。


⑤给定飞行时间,实际上就确定了两点之间的平近点角差,因为

所以
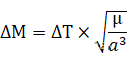

三、算法描述
根据以上的分析,设计了相应的算法。
算法1:基于飞行时间的真近点角差计算算法
算法概述:基于飞行时间,计算发射点和落点的真近点角差。目的是用于与前述利用余弦定理得到的真近点角进行比较。
输入:半长轴a,偏心率e,通径r
输出:真近点角差
算法如下:
(1)根据发射点的半长轴a,偏心率e,通径r,计算发射点的平近点角M_F和真近点角F_F;
(2)根据前述∆M,得到落点的平近点角M_L=M_F+∆M;
(3)根据M_L,反算落点的偏近点角E_L;
(4)根据E_L,反算落点的真近点角F_L;
(5)返回F_L-F_F。
上述算法代表了本文中的一个比较重要的思路,即“基于飞行时间的真近点角差”,基于此值与“基于余弦定理的真近点角差”的比较,来决定偏心率搜索的策略。
算法2:偏心率递归搜索算法
给定半长轴a,计算满足飞行时间和真近点角差2个条件的e值,并判定此时导弹是否飞抵落点。
输入:给定惯性系下发射点位置、落点位置、飞行时间、半长轴a
输出:满足时间约束的e值,以及导弹是否飞抵落点的标志。规则为:无法找到满足飞行时间和真近点角差2个条件的e,返回false;否则,返回true,但另外提供一个标志值,返回0表示给定飞行时间恰好到达落点;返回-1表示给定时间已经飞过落点,返回1表示尚未到达落点。
采用递归实现,其伪代码形式如下
bool recursiveCalculateE(double a, double eMin, double eMax,double launchRa,double impactRa,double deltaTrueAnomaly, double& e, int& tag){
if (fabs(eMax - eMin) < 1e-8)//找不到满足2个条件的e值
return false;
double em = (eMin + eMax) / 2;
调用算法1,计算em对应的基于飞行时间的真近点角差deltaTAm
if (fabs(deltaTAm - deltaTrueAnomaly) < 1e-5) {//满足飞行时间和真近点角差2个条件
基于a、r、e计算发射点和落点的平近点角;
根据平近点角计算发射点和落点的飞行时间flyTime,与目的飞行时间_flyTime比较;
if (fabs(_flyTime - flyTime) < 1e-3)
tag = 0;
else if ( _flyTime > flyTime )
tag = 1;
else tag = -1;
return true;}
调用算法1,计算eMin对应的基于飞行时间的真近点角差deltaTAmin;
调用算法1,计算eMax对应的基于飞行时间的真近点角差deltaTAmax;
if (deltaTAm > deltaTrueAnomaly){
if (deltaTAmin < deltaTrueAnomaly && deltaTAmax < deltaTrueAnomaly){
int tag0 = recursiveCalculateE(a, em, eMax,launchRa,impactRa,deltaTrueAnomaly, e, tag);
int tag1 = recursiveCalculateE(a, eMin, em, launchRa, impactRa, deltaTrueAnomaly, e, tag);
return tag1 || tag0;}
else if (deltaTAmin < deltaTrueAnomaly)
return recursiveCalculateE(a, eMin, em, launchRa, impactRa, deltaTrueAnomaly, e, tag);
else
return recursiveCalculateE(a, em, eMax, launchRa, impactRa, deltaTrueAnomaly, e, tag);}
else {略}}
上述算法的说明:
(1)当e值满足飞行时间和真近点角差两个条件时,并不一定此时对应的点即为落点。实际上,几乎在某个很大范围内的所有a值,都能找到满足这两个条件的e。因此还需要判断发射点经过给定飞行时间后到达的点是否就是落点。在本文中是通过比较飞行时间确定的。
(2)在进行基于飞行时间的真近点角差与基于余弦定理的真近点角差进行比较的时候,其大小关系与e并不是一种线性关系。即:记两个真近点角差为∆∆F,那么,无法确保在eMin到eMax之间,∆∆F单调递增或单调递减。因此,在递归过程中,需要根据eMin、em、eMax三者对应的∆F值,采用不同的递归策略,有的情况折半递归,有的情况需要向2个方向递归。
算法3:半长轴搜索算法
给定惯性系发射点和落点坐标、飞行时间,搜索计算半长轴a和偏心率e。
输入:给定发射点位置、落点位置、飞行时间
输出:半长轴a和偏心率e
伪代码如下
bool MissileTrajectoryModel_FixedFlyTime::calculateAE(double& a, double &e){
CVector3D launchPos, impactPos;
LB2DD(_launchLatitude, _launchLongitude, _launchAltitude, launchPos.x, launchPos.y, launchPos.z);
LB2DD(_impactLatitude, _impactLongitude + _flyTime * (EARTH_ROTATE_SPEED*180.0 / osg::PI), _impactAltitude, impactPos.x, impactPos.y, impactPos.z);//惯性系
double launchRa = launchPos.GetLength () / 1000.0;
double impactRa = impactPos. GetLength () / 1000.0;
double dis = (launchPos-impactPos).GetLength() / 1000.0;
double deltaTrueAnomaly = acos((launchRa*launchRa + impactRa * impactRa - dis * dis) / (2 * launchRa*impactRa));
double a0 = calculateMinA(launchRa, impactRa,dis)+1e-3;
double a1 = 36000.000;
bool res0 = calculateEbyA(launchRa, impactRa, dis, deltaTrueAnomaly, a0, e0, tag);
bool res1 = calculateEbyA(launchRa, impactRa, dis, deltaTrueAnomaly, a1, e1, tag);
while (true){
double amid = (a0 + a1) / 2;
double emid;
int tag;
bool res = calculateEbyA(launchRa, impactRa, dis, deltaTrueAnomaly, amid, emid, tag);
if (res) {
if (tag == 0){
a = amid;
e = emid;
return true;}
else if ( tag == -1 )//向下搜索
a1 = amid;
else
a0 = amid;
}
else
a0 = amid;
if (fabs(a1 - a0) < 1e-8)return false;}}
对于给定的飞行时间,并非一定可以搜索到结果,此时会返回false。利用返回值,可以用于计算给定发射点和落点情况下飞行时间的范围。
同时在本文算法中,限定了最大的半长轴值,因为很大的值对于弹道仿真来说并无太大意义。半长轴的最小值则是根据给定的发射点和落点,计算其合法的偏心率范围,以此来得到最小值。
四、仿真结果
下面给出仿真结果,并同时给出计算的a、e值与STK的对比。发射点(0,0,0),落点(30,10,0)。

上图中给定的飞行时间为1000秒。本文算法计算得到的半长轴为4165.2965,偏心率为0.70285362。STK中模型的半长轴为4165.3,偏心率为0.702854。

上图中给定的飞行时间为4000秒。本文算法计算得到的半长轴为6368.92404,偏心率为0.91500638。STK中模型的半长轴为6368.92,偏心率为0.915006。

上图中给定的飞行时间为10000秒。本文算法计算得到的半长轴为10699.3805,偏心率为0.92073491。STK中模型的半长轴为10699.4,偏心率为0.920735。

上图中给定的飞行时间为20000秒。本文算法计算得到的半长轴为16501.8713,偏心率为0.89685717。STK中模型的半长轴为16501.9,偏心率为0.896857。
本文算法与STK的ae结果,存在微小的差异(当然,如果本文算法a,e值均按STK所显示的位数的话,是完全一致的)。
此外,在计算得到的最短飞行时间方面,同样是上述的发射点和落点,本文算法计算得到的为756.2秒,而STK得到的为470.033秒。
与Lambert模型相比,本文算法简单,但缺乏理论上的分析。本文的2次搜索中分别利用真近点角差和飞行时间差进行了折半的搜索,这可能会出现搜索不正确的情况,而最短飞行时间与STK的不同即为此。
此外,分别利用了Gauss方程(《近地航天器轨道基础》)、Lambert时间方程(《近地航天器轨道基础》)和变形的Lambert时间方程(哈工大博士论文《航天器自主交会对接制导与控制方法研究》)进行了计算。Gauss方程对于小一点的飞行时间较为友好,但大约到2000秒以上时就再也无法收敛了。直接利用Lambert时间方程,完全解不出。变形Lambert时间方程对各种情况均较为友好,比本文算法的适用性更强。























 2337
2337

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








