多智能体强化学习(四)多智能体RL
在多智能体场景中,就像在单智能体场景中一样,每个智能体都在尝试通过试错程序来解决顺序决策问题。不同的是,环境状态的演变和每个智能体收到的奖励功能现在由所有智能体的联合行动决定(见图3)。因此,智能体不仅需要考虑环境,还需要考虑其他学习代理交互。一个涉及多个智能体的决策过程通常通过一个随机游戏来建模(沙普利,1953),也被称为马尔可夫游戏(利特曼,1994)。
1. 问题的公式:随机博弈
定义2(随机博弈)随机博弈可以看作是定义1中MDP的多人博弈扩展。因此,它也由一组关键元素定义, < N , S , A i { i ∈ 1 , … , N } , P , { R i } i ∈ { 1 , … , N } , γ > <N,\mathbb{S},{A^i}_{\{i∈{1,…,N}\}},P,\{R^i\}_{i∈{\{1,…,N\}}},γ> <N,S,Ai{i∈1,…,N},P,{Ri}i∈{1,…,N},γ>。
- N:智能体的数量,N=1退化为单智能体MDP,N>>2在本文称为多智能体情况。
- S \mathbb S S:所有智能体共享的环境状态集。
- A \mathbb A A::智能体 i i i的动作集。我们表示 A \mathbb A A:= A 1 \mathbb A^1 A1×···× A N \mathbb A^N AN。
- P : S × A × S → ∆ ( S ) P:\mathbb S×A ×\mathbb S→∆(\mathbb S) P:S×A×S→∆(S):对于每个时间步骤 t ∈ N t∈\mathbb N t∈N,给定智能体的联合动作为 a ∈ A a∈\mathbb A a∈A,在下一个时间步骤中从状态 s ∈ S s∈\mathbb S s∈S到状态 s ′ ∈ S s'∈\mathbb S s′∈S的转换概率。
- R i : S × A × S → R R^i:\mathbb S× \mathbb A× \mathbb S→\mathbb R Ri:S×A×S→R:从 ( s , a ) (s,a) (s,a)到 s ′ s' s′转换的第 i i i个智能体返回的奖励函数标量值。奖励的绝对值一致受 R m a x R_{max} Rmax为界。
- γ ∈ [ 0 , 1 ] γ∈[0,1] γ∈[0,1]是表示时间值的折扣系数。
当有必要区分智能体 i i i和所有其他 N − 1 N−1 N−1的对手时,我们使用 ( ⋅ i , ⋅ − i ) (·^i, ·^{−i}) (⋅i,⋅−i)(例如, a = ( a i , a − i ) ) a=(a^i, a^{−i})) a=(ai,a−i))的上标。
最终,随机博弈(SG)作为一个框架,允许在决策场景中同时从智能体进行移动。该游戏可以按顺序描述如下:在每个时间步长
t
t
t中,环境都有一个状态
s
t
s_t
st,并且给定
s
t
s_t
st,每个智能体与所有其他智能体同时执行其操作
a
t
i
a^i_t
ati。所有智能体的联合行动使环境过渡到下一个状态
s
t
+
1
∼
P
(
⋅
∣
s
t
,
a
t
)
s_{t+1}∼P(·|s_t,a_t)
st+1∼P(⋅∣st,at);然后,环境决定了对每个智能体的即时奖励
R
i
(
s
t
、
a
t
、
s
t
+
1
)
R^i(s_t、a_t、s_{t+1})
Ri(st、at、st+1)。正如在单智能体MDP场景中所看到的,每个智能体
i
i
i的目标都是解决SG。换句话说,每个智能体的目标是找到一个行为策略(或者,博弈论中的混合策略术语)。也就是说,
π
i
∈
Π
i
:
S
→
∆
(
A
i
)
π^i∈Π^i:S→∆(\mathbb A^i)
πi∈Πi:S→∆(Ai),它可以指导智能体采取顺序行动,以便获得等式(12)中的折扣累积奖励已最大化。在这里,∆(·)是一个集合上的概率单形。在博弈论中,如果∆(·)被狄拉克测度所取代,
π
i
π^i
πi也被称为纯策略(vs混合策略)。
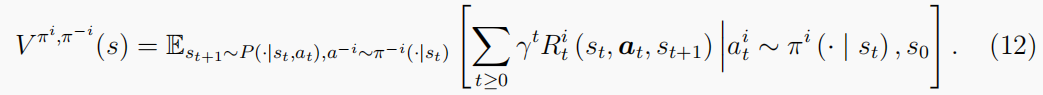
等式(12)的比较与等式(4)一起使用指出,每个智能体的最优策略不仅受到其自身策略的影响,而且也受到游戏中其他智能体的策略的影响。这种情况导致了单智能体RL和多智能体RL之间的解决方案概念上的根本差异。
2. 解决随机对策
一个SG可以看作是一系列正常形式的对策,这是一种可以在矩阵中表示的对策。以原始交叉口场景为例(见图4)。SG在时间t的快照(阶段游戏)可以表示为矩阵格式的正常形式的游戏。这些行对应于智能体 1 1 1的动作集 A 1 \mathbb A^1 A1,并且这些列对应于代理2的动作集 A 2 \mathbb A^2 A2。矩阵的值是对每个联合动作对的奖励。在这种情况下,如果两个智能体只关心最大化自己可能的奖励,而不考虑其他智能体(单智能体RL问题中的解决方案概念),并选择匆忙的动作,它们将达到相互碰撞的结果。显然,这种状态是不安全的,因此对每个智能体都是次优的,尽管每个智能体在匆忙时可能的奖励是最高的。因此,为了解决销售问题并真正最大化累积奖励,每个智能体在决定其政策时必须考虑他人采取战略行动。
不幸的是,与具有多项式可解时间的线性编程公式的MDPs相比,求解SGs通常涉及到应用牛顿方法来求解非线性程序。然而,有两种特殊的双人游戏获得折扣奖励的SGs情况是它仍然可以写成LPs(肖汉姆和莱顿-布朗,2008年,第6.2章)。内容如下:
- 单控制器SG:如果向量 a a a中的第 i i i指数是 a [ i ] = a i , ∀ s ∈ S , ∀ a ∈ A a[i]=a^i,∀s∈\mathbb S,∀a∈\mathbb A a[i]=ai,∀s∈S,∀a∈A,则确定 P ( ⋅ ∣ a , s ) = P ( ⋅ ∣ a i , s ) P(·|a,s)=P(·|a^i,s) P(⋅∣a,s)=P(⋅∣ai,s)。
- 可分离的奖励状态独立的过渡(SR-SIT)SG ,例如:状态和行为对奖励函数有独立的影响,而转换函数仅依赖于联合行为。
2.1 基于价值的MARL方法
等式(7)中的单智能体Q-学习更新在多智能体的情况下仍然有效。在第
t
t
t次迭代中,对于每个智能体
i
i
i,给定从重播缓冲区采样的转换数据
{
(
s
t
,
a
t
,
R
i
,
s
t
+
1
)
}
t
≥
0
\{(s_t,a_t,R^i,s_{t+1})\}_{t≥0}
{(st,at,Ri,st+1)}t≥0,它只更新
Q
(
s
t
,
a
t
)
Q(s_t,a_t)
Q(st,at)的值,并保持q函数的其他条目不变。具体来说,我们有
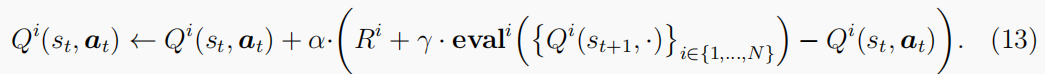
与等式(7)相比,最大运算符被更改为
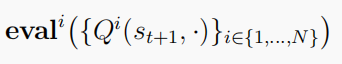
在等式(13)中来反映这样一个事实,即每个智能体不能只考虑自己,而必须通过考虑所有智能体在
t
+
1
t+1
t+1的价值,以他们的q函数集表示。然后,就可以解决最优策略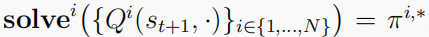
因此,我们可以进一步将评估运算符写为
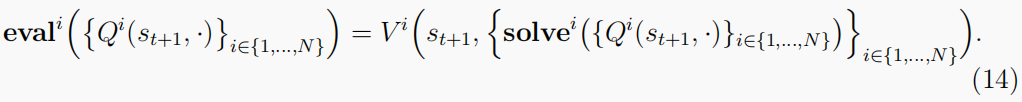
总之,
s
o
l
v
e
i
solve^i
solvei在某个平衡点返回智能体最优策略的一部分(不一定对应于其最大的可能回报),而
e
v
a
l
i
eval^i
evali给智能体在这种平衡下我的预期长期回报,假设所有其他智能体都同意发挥相同的平衡。
2.2 基于策略的MARL方法
由于多智能体系统的组合性质,该基于价值的方法受到了维数的诅咒(有关进一步的讨论,请见第4.1节)。这一特性需要开发基于策略的函数逼近算法。具体地说,每个智能体通过更新例如神经网络的参数
θ
i
θ^i
θi来学习自己的最优策略
π
θ
i
i
:
S
→
∆
(
A
i
)
π^i_{θ^i}:\mathbb S→∆(\mathbb A^i)
πθii:S→∆(Ai)。让
θ
=
(
θ
i
)
i
∈
{
1
,
…
…
,
N
}
θ=(θ^i)_{i∈\{1,……,N\}}
θ=(θi)i∈{1,……,N}表示所有智能体的策略参数的集合,并让
π
θ
:
=
∏
{
i
∈
1
,
…
…
,
N
}
π
θ
i
i
(
a
∣
i
)
π_θ:=\prod_{\{i \in{1,……,N}\}}π^i_{θ^i} (a^|i)
πθ:=∏{i∈1,……,N}πθii(a∣i)是联合策略。为了优化参数
θ
i
θ^i
θi,可以将第2.3.2节中的策略梯度定理扩展到多智能体上下文。给定代理
i
i
i的目标函数
J
i
(
θ
)
=
E
s
∼
P
,
a
∼
π
θ
∑
t
>
=
0
γ
t
R
t
i
J^i(θ)=\mathbb E_{s∼P, a∼π_θ}\sum_{t>=0}\gamma_tR^i_t
Ji(θ)=Es∼P,a∼πθ∑t>=0γtRti,有:
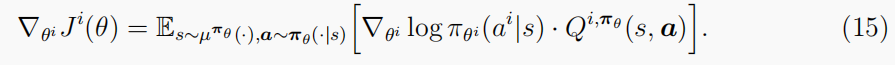
考虑一个具有确定性策略的连续动作集,我们将多主体确定性策略梯度(MADDPG)(Lowe等人,2017)写为
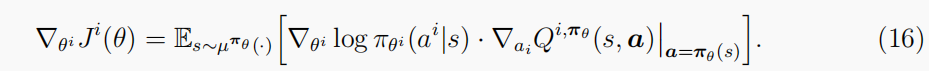
请注意,在这两个问题中。(15)&(16),对联合策略
π
θ
π_θ
πθ的期望意味着必须遵守其他代理的策略;对于许多实际应用程序,这通常是一个强有力的假设。
2.3 纳什均衡的求解概念
博弈论在多智能体学习中扮演着重要的作用,它提供了所谓的解决方案概念,通过展示玩家最终将采用哪些策略来描述游戏的结果。MARL存在许多类型的解概念(见第4.2节),其中最著名的可能是非合作博弈论中的纳什均衡(NE)(Nash,1951)。“非合作”一词并不意味着智能体不能一直合作或必须相互争斗,它只是意味着每个智能体独立地最大化自己的奖励,智能体不能组成联盟来做出集体决定。
在一个正常形式的博弈中,NE描述了联合策略轮廓的一个平衡点
(
π
1
,
∗
,
…
,
π
N
,
∗
)
(π^{1,∗},…,π^{N,∗})
(π1,∗,…,πN,∗),其中每个智能体根据它们对其他智能体的最佳反应行事。一旦考虑了所有其他玩家的策略,最佳的反应就会为玩家产生最佳的结果。玩家
i
i
i对
π
−
i
π^{−i}
π−i的最佳响应是一组满足以下条件的策略。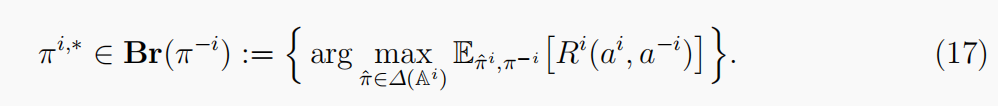
NE 指出,如果所有的玩家都是完全理性的,他们中没有一个会有动机偏离他们最好的反应,
π
i
,
∗
π^{i,∗}
πi,∗,因为其他人正在玩
π
−
i
,
∗
π^{−i,∗}
π−i,∗。请注意,NE是根据最佳响应来定义的,这依赖于相对的奖励值,这表明识别NE并不需要奖励的确切值。事实上,NE在玩家奖励函数的正仿射变换下是不变的。应用布鲁维尔不动点定理,纳什(1951)证明了任何具有有限作用集的博弈都始终存在混合策略NE。在驾车穿过图4中的十字路口的示例中,NE为(屈服、冲)和(冲、屈)。
对于SG,一个常用的平衡是ne的更强版本,称为马尔可夫完美NE(马斯金和Tirore,2001),定义为:
定义3(随机对策的纳什均衡)马尔可夫策略
π
∗
=
(
π
i
,
∗
,
π
−
i
,
∗
)
π^∗=(π^{i,∗},π^{−i,∗})
π∗=(πi,∗,π−i,∗)是在定义2中定义的SG的马尔可夫完美NE。
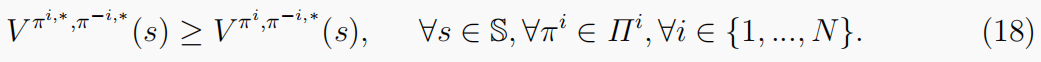
“马尔可夫政策”是指纳什政策对于可能的历史的特定划分是可衡量的(通常指的是最后一个状态)。“完美”这个词的意思是,无论开始状态如何,平衡状态也是子博弈完美的(Selten,1965年)。考虑到SGs的顺序性质,这些假设是必要的,同时仍然保持着普遍性。此后,马尔可夫完美NE将被称为NE。对于折扣和平均奖励的SGs,始终存在混合策略NE,虽然它们可能不是唯一的。事实上,检查唯一性是NP-hard(科尼策和桑德霍尔姆,2002年)。以NE为最优性的求解概念,我们可以重写等式(14),视为:
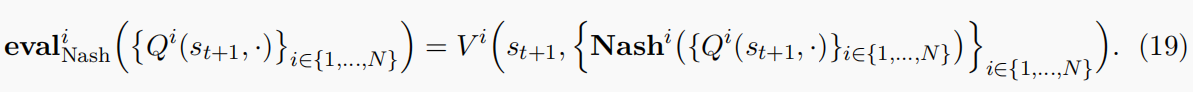
在上述方程中,
N
a
s
h
i
(
⋅
)
=
π
i
,
∗
Nash^i(·)=π^{i,∗}
Nashi(⋅)=πi,∗计算agent
i
i
i策略的NE,
V
i
(
s
,
{
N
a
s
h
i
}
i
∈
{
1
,
…
…
,
N
}
)
V^i(s,\{{ Nash^i}\}_{i∈{\{1,……,N\}}})
Vi(s,{Nashi}i∈{1,……,N})是在状态s下agent i的预期回报。等式(19)和等式(13)构成了纳什Q-学习的学习步骤(Hu等人,1998)。这个过程本质上导致了一组学习的最优策略的结果,对于遇到的每一个单阶段游戏都达到NE。在NE不是唯一的情况下,Nash-Q采用手工制作的规则进行均衡选择(例如,所有玩家都选择第一个NE)。此外,与正常的Q学习相似,在等式中定义的Nash-Q算子(20)也被证明是一个收缩映射,当NE唯一时,随机更新规则在所有状态下都收敛于NE:
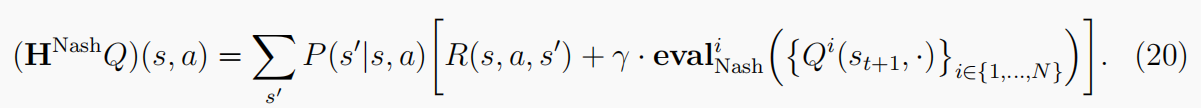
在二人general-sum博弈中寻找NE的过程可以表述为线性互补问题(LCP),然后用莱姆克豪森算法求解(沙普利,1974)。然而,拥有三名以上玩家的游戏的确切解决方案是未知的。事实上,寻找NE的过程对计算要求很高。即使在双人游戏的情况下,求解NE的复杂性也是P P AD-hard(有向图上的多项式奇偶校验参数)(陈和邓,2006;Daskalakis等人,2009);因此,在最坏的情况下,解决方案可能需要时间与游戏大小呈指数级的。这种复杂性禁止任何暴力或详尽的搜索解决方案,除非P=NP(见图5)。正如我们所期望的那样,对于一般的SGs来说,NE要困难得多,其中确定一个纯策略的NE是否存在是P SP ACE-hard。即使SG有一个有限的时间范围,计算仍然是NP-hard(科尼策和桑德霍尔姆,2008)。当提到对NE的近似方法,最著名的多项式可计算算法可以在双矩阵博弈上实现=0.3393(Tsaknakis和Spirakis,2007);它的方法是把寻找网元的问题变成一个寻找平稳点的优化问题。
图5:不同复杂性类的景观。相关例子包括1)解决双人零和博弈中的NE,P-complete(Noumann,1928),2)在一般和博弈中求解NE的问题(PPKalakis等人,2009),3)检查NE的唯一性(Conizer和桑德霍尔姆,2002),4)检查纯策略NE是否存在于随机博弈,PSPACE-hard(科尼策尔和桑德霍尔姆,2008)和5)解决Dec-POMDP,NEXPTIME-Hard(Bern斯坦等人,2002)。
2.4 特殊类型的随机策略
要总结SGs的解决方案,可以想到“master”方程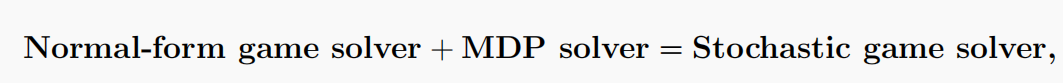
Bowling和Veloso(2000)首先总结了它(见表4)。第一项是指解决在每个时间步长中遇到的阶段博弈的平衡(NE)。它假设过渡和奖励功能是已知的。第二个术语是指应用RL技术(如Q-elaring)在序列决策过程中对时间结构进行建模。它假设只接受对过渡和奖励功能的观察。两者的结合给出了SGs的解决方案,智能体到达游戏中每一个步的某种类型的平衡。
图6:POSGs中不同类型游戏的维恩图。SG和Dec-POMDP的交集是团队游戏。在上半段的SG中,我们有MDP⊂团队游戏⊂潜在游戏⊂相同感兴趣的游戏⊂SGs,和零和游戏⊂SGs。在Dec-POMDP的下半段,我们有MDP⊂团队游戏⊂Dec-MDP⊂Dec-POMDP,和MDP⊂POMDP⊂Dec-POMDP。关于这些游戏的详细定义,我们参考章节(3.2.4和3.2.5)。
由于用网NE作为正常形式博弈的解概念求解一般SGs在计算上具有挑战性,研究人员的目标是研究具有可处理解概念的特殊类型的SGs。在本节中,我们提供了这些特殊类型的游戏的简要总结。
定义4(随机对策的特殊类型)给定了定义2中SG的一般形式,我们有以下特殊情况:
- 正常形式的游戏/重复游戏:|S|=1,见图4中的示例。这些游戏只有一个状态。虽然理论上没有基础,但它实际上更容易解决一个小规模SG的问题。
- 相同利益设置:智能体共享相同的学习目标,我们表示为R。由于所有智能体都是独立处理的,每个智能体都可以安全地选择最大化自己奖励的动作。因此,单智能体RL算法可以安全地应用,并开发了一种分散的方法。有几种类型的SGs属于这一类。
- 团队游戏/完全合作的游戏/多智能体MDP(MMDP):智能体被认为是同质的和可互换的,所以重要的是,它们共享相同的奖励功能, R = R 1 = R 2 = ⋅ ⋅ ⋅ = R N R=R^1=R^2=···=R^N R=R1=R2=⋅⋅⋅=RN。
- 团队平均奖励游戏/网络多智能体MDP(M-MDP):智能体可以有不同的奖励功能,但他们有相同的目标, R = 1 / N ∑ i = 1 N R i R=1/N\sum ^N_{i=1}R^i R=1/N∑i=1NRi。
- 随机势博弈:智能体可以有不同的奖励函数,但它们的共同利益由共享势函数
R
=
φ
R=φ
R=φ描述,定义为
φ
:
S
×
A
→
R
φ:\mathbb S× \mathbb A→ \mathbb R
φ:S×A→R,使
∀
(
a
i
,
a
−
i
)
,
(
b
i
,
b
−
i
)
∈
A
,
∀
i
∈
{
1
,
…
,
N
}
,
∀
∈
S
∀(a^i,a^{−i}),(b^i,b^{−i})∈\mathbb A,∀i∈{\{1,…,N\}},∀∈\mathbb S
∀(ai,a−i),(bi,b−i)∈A,∀i∈{1,…,N},∀∈S和以下方程式成立:
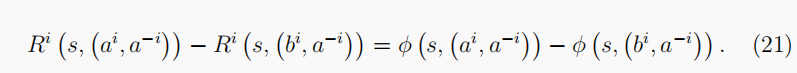 这类类型的游戏保证具有纯策略NE(Mguni,2020)。此外,如果选择奖励函数作为潜在函数,潜在游戏就会退化为团队游戏。
这类类型的游戏保证具有纯策略NE(Mguni,2020)。此外,如果选择奖励函数作为潜在函数,潜在游戏就会退化为团队游戏。
- 零和设置:智能体共享相反的利益并具有竞争力,每个智能体针对最坏情况进行优化。由于Neoumann(1928)提出的极大极小定理,可以在多项式时间内使用线性程序(LP)来求解。最小-最大值的概念也与机器学习中的鲁棒性有关。我们可以细分零和设置如下:
- 双人constant-sum游戏: R 1 ( s 、 a 、 s ′ ) + R 2 ( s 、 a 、 s ′ ) = c , ∀ ( s 、 a 、 s ′ ) R^1(s、a、s')+R^2(s、a、s')=c, ∀(s、a、s') R1(s、a、s′)+R2(s、a、s′)=c,∀(s、a、s′),其中c是一个常数,通常是c=0。对于 c ≠ 0 c\ne0 c=0的情况,人们总是可以减去所有回报条目的常数c,使游戏为零和。
- 两队的竞争性比赛:两支球队互相竞争,队号分别为
N
1
N_1
N1和
N
2
N_2
N2。他们的奖励功能是:
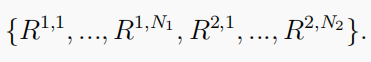
一个团队中的团队成员共享相同的目标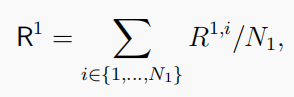 或者
或者
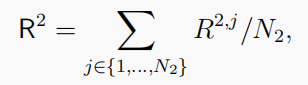
和 R 1 + R 2 = 0 R^1+ R^2=0 R1+R2=0。 - 调和游戏:任何正常形式的游戏都可以分解为潜在游戏和调和游戏(Candogan等人,2011)。一种调和对策(例如,岩石剪刀布)可以看作是一类具有调和性质的一般零和对策。让
∀
p
∈
A
∀p∈\mathbb A
∀p∈A是一个联合的纯策略配置文件,并让
A
[
−
i
]
=
{
q
∈
A
:
q
i
≠
p
i
,
q
−
i
=
p
−
i
}
\mathbb A^{[−i]}={\{q∈ \mathbb A:q^i\ne p^i,q^{−i}=p^{−i}\}}
A[−i]={q∈A:qi=pi,q−i=p−i}是与智能体
i
i
i上的
p
p
p不同的策略集;然后,谐波性质是:
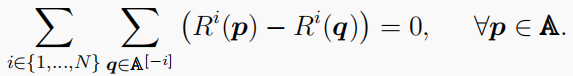
- 线性二次(LQ)设置:过渡模型遵循线性动力学,奖励函数相对于状态和动作是二次的。与黑盒奖励功能相比,LQ游戏提供了一个简单的设置。例如,已知的演员-批评家方法可以促进收敛到零和LQ对策的NE(Al-Tamimi等人,2007)。同样,LQ设置也可细分如下:
- 双人零和LQ游戏:
Q
∈
R
∣
S
∣
、
U
1
∈
R
∣
A
1
∣
和
W
2
∈
R
∣
A
2
∣
Q∈\mathbb R^{|S|}、U^1∈\mathbb R^{|A^1|}和W^2∈\mathbb R^{|A^2|}
Q∈R∣S∣、U1∈R∣A1∣和W2∈R∣A2∣分别是状态空间和动作空间的已知成本矩阵,而矩阵
A
∈
R
∣
S
∣
×
∣
S
∣
、
B
∈
R
∣
S
∣
×
∣
A
1
∣
、
C
∈
R
∣
S
∣
×
∣
A
2
∣
A∈R^{|S|×|S|}、B∈R^{|S|×|A^1|}、C∈R^{|S|×|A^2|}
A∈R∣S∣×∣S∣、B∈R∣S∣×∣A1∣、C∈R∣S∣×∣A2∣通常是未知的。
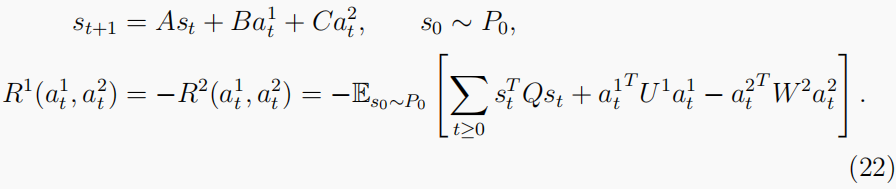
- 多人general-sumLQ游戏:关于双人游戏的区别在于,智能体奖励的总和不一定等于零:
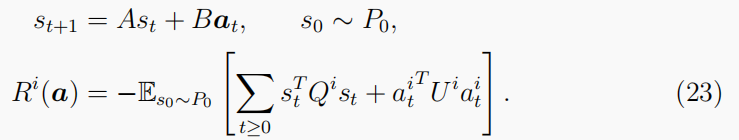
- 双人零和LQ游戏:
Q
∈
R
∣
S
∣
、
U
1
∈
R
∣
A
1
∣
和
W
2
∈
R
∣
A
2
∣
Q∈\mathbb R^{|S|}、U^1∈\mathbb R^{|A^1|}和W^2∈\mathbb R^{|A^2|}
Q∈R∣S∣、U1∈R∣A1∣和W2∈R∣A2∣分别是状态空间和动作空间的已知成本矩阵,而矩阵
A
∈
R
∣
S
∣
×
∣
S
∣
、
B
∈
R
∣
S
∣
×
∣
A
1
∣
、
C
∈
R
∣
S
∣
×
∣
A
2
∣
A∈R^{|S|×|S|}、B∈R^{|S|×|A^1|}、C∈R^{|S|×|A^2|}
A∈R∣S∣×∣S∣、B∈R∣S∣×∣A1∣、C∈R∣S∣×∣A2∣通常是未知的。
2.5 部分可观测的设置
一个部分可观察的随机博弈(POSG)假设代理不能访问精确的环境状态,而只能通过观察函数观察真实状态。形式上,此方案的定义为:
定义5(部分可观测的随机对策) POSG由集合定义
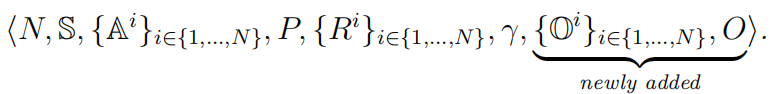 除了在定义2中定义的SG外,POSG还添加了以下术语:
除了在定义2中定义的SG外,POSG还添加了以下术语:
- O i \mathbb O^i Oi:每个代理的观察集。联合观测集定义为 O : = O 1 × ⋅ ⋅ ⋅ × O N \mathbb O:=\mathbb O^1×···×\mathbb O^N O:=O1×⋅⋅⋅×ON。
- O : S × A → ∆ ( O ) \mathbb O:S×\mathbb A→∆(\mathbb O) O:S×A→∆(O):观察函数 O ( o ∣ a , s ′ ) O(o|a,s') O(o∣a,s′)表示给定动作为a∈A的观察o∈O的概率,以及来自环境过渡的新状态 s ′ ∈ S s'∈\mathbb S s′∈S。
每个代理的策略现在都会更改为 π i ∈ Π i : O → ∆ ( A i ) π^i∈Π^i:\mathbb O→∆(\mathbb A^i) πi∈Πi:O→∆(Ai)。
虽然添加的部分可观察性约束在许多实践中的实际应用中很常见,但理论上它加剧了解决SGs的困难。甚至在最简单的双人游戏完全合作的有限视野博弈的设置中,解决POSG是NEXP-hard(见图5),这意味着在最坏情况下解决POSG需要超指数时间(伯恩斯坦等人,2002)。然而,在部分可观察的设置下研究游戏的好处来自于算法的优势。Centralised-training-with-decentralised-execution方法(福斯特等,2017a;劳等,2017;奥利ehoek等,2016;拉希德等,2018;杨等,2020)取得了许多经验成功,与DNNs一起充满希望。
POSG是最一般的游戏类之一。POSGs的一个重要子类是分散的部分可观察的MDP(Dec-POMDP),其中所有的代理都共享相同的奖励。在形式上,此方案的定义如下:
定义6(Dec-POMDP) Dec-POMDP是定义5中定义的 特殊型 当 R 1 = = R 2 ⋅ ⋅ ⋅ = R N R^1==R^2···=R^N R1==R2⋅⋅⋅=RN。
Dec-POMDPs通过部分可观察性条件与单代理MDPs相关,通过假设相同的奖励,它们也与随机团队博弈相关。换句话说,单代理MDPs和随机团队游戏的版本都是特定类型的Dec-POMDPs(见图6)。

定义7(特殊类型的POMDPs) 以下博弈是特殊类型的Dec-POMDPs.。
- 部分可观察到的MDP(POMDP):只有一个令人感兴趣的代理,N=1。这种情况相当于定义1中具有部分可观察性约束的单代理MDP。
- 分散的MDP(Dec-MDP):Dec-MDP中的代理具有共同的完全可观测性。也就是说,如果所有的代理分享他们的观察结果,他们可以一致恢复Dec-MDP的状态。数学上,我们有 ∀ o ∈ O , ∃ ∈ S , 这 样 P ( S t = ∣ O t = o ) = 1 ∀o∈O,∃∈S,这样P(S_t=|O_t=o)=1 ∀o∈O,∃∈S,这样P(St=∣Ot=o)=1。
- 完全合作的随机博弈:假设每个代理都有完全的可观察性, ∀ i = { 1 , … , N } , ∀ o i ∈ O i , ∃ ∈ S , 使 P ( S t = ∣ O t = o i ) = 1 ∀_i=\{1,…,N\},∀o^i∈O^i,∃∈\mathbb S,使P(S_t=|O_t=o_i)=1 ∀i={1,…,N},∀oi∈Oi,∃∈S,使P(St=∣Ot=oi)=1。定义4中的完全合作的SG是一种Dec-POMDP。






















 1256
1256











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








