文章目录
一、课本概念及公式
3.1 平面图及其平面嵌入
平面图的定义
3.2 平面图欧拉公式
公式
3.3 极大平面图
面的次数和桥的概念
平面图的各个面的边数和与边满足的关系
即：
∑
i
=
1
ϕ
d
(
f
i
)
=
2
ε
\sum_{i=1}^{\phi} d\left(f_{i}\right)=2 \varepsilon
∑i=1ϕd(fi)=2ε
推论3.1
证明：
若非连通图时，可以分成多个连通片，有：
推论3.2
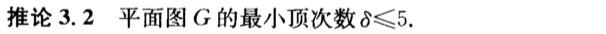
证明：
由
：
{
ε
⩽
3
ν
−
6
∑
v
∈
V
(
G
)
d
(
v
)
=
2
ε
∑
v
∈
V
(
G
)
d
(
v
)
⩾
δ
ν
由：\left\{\begin{array}{c} \varepsilon \leqslant 3\nu-6 \\ \sum_{v \in V(G)} d(v)=2 \varepsilon \\ \sum_{v \in V(G)} d(v) \geqslant \delta \nu \end{array}\right.
由：⎩⎨⎧ε⩽3ν−6∑v∈V(G)d(v)=2ε∑v∈V(G)d(v)⩾δν
得 ： δ ν ⩽ 2 ε ⩽ 2 ( 3 ν − 6 ) δ ⩽ 6 − 12 ν 得：\begin{aligned} \delta \nu & \leqslant 2 \varepsilon \leqslant 2(3 \nu-6) \\ \delta & \leqslant 6-\frac{12}{\nu} \end{aligned} 得：δνδ⩽2ε⩽2(3ν−6)⩽6−ν12
极大平面图定义
定理3.3，极大平面图的充要条件
证明：
充分性，即证若存在G的平面嵌入G`的每个面都是三角形，则G是极大平面图：
{
d
(
f
)
=
3
①
∑
f
∈
F
(
G
)
d
(
f
)
=
2
ε
②
ν
−
ε
+
ϕ
=
2
③
\left\{\begin{array}{l}d(f)=3 \quad \text { ① } \\ \sum_{f \in F(G)} d(f)=2 \varepsilon \text { ② } \\ \nu-\varepsilon+\phi=2 \text{ ③ } \end{array}\right.
⎩⎨⎧d(f)=3 ① ∑f∈F(G)d(f)=2ε ② ν−ε+ϕ=2 ③
联立①②得： 3 ϕ = 2 ε 3 \phi=2 \varepsilon 3ϕ=2ε
代入③消去φ得： ε = 3 ν − 6 \varepsilon=3 \nu-6 ε=3ν−6
由推论3.1知 ε ⩽ 3 ν − 6 \varepsilon \leqslant 3 \nu-6 ε⩽3ν−6，故边已经达到上界，故G是极大平面图
必要性，即证G是极大平面图，则G的平面嵌入G`的每个面都是三角形：
推论3.3(极大平面图的充要条件公式表达)和定理3.4
3.4 平面图的充要条件
证明k3,3不是平面图
反证法：
{ d ( f ) ⩾ 4 ① ∑ d ( f ) = 2 ε ② \left\{\begin{array}{l}d(f) \geqslant 4 \quad \text{ \ \ \ \ \ \ \ ①} \\ \sum d(f)=2 \varepsilon \text{ \ \ \ \ ②} \end{array}\right. {d(f)⩾4 ①∑d(f)=2ε ②
得： 4 ϕ ⩽ 18 , ϕ ⩽ 4 4 \phi \leqslant 18, \phi \leqslant 4 4ϕ⩽18,ϕ⩽4
再结合 ε = 9 , ν = 6 \varepsilon=9, \nu=6 ε=9,ν=6 和 ν − ε + ϕ = 2 \nu-\varepsilon+\phi=2 ν−ε+ϕ=2 得： 6 − 9 + 4 ⩾ 2 6-9+4 \geqslant 2 6−9+4⩾2
推出矛盾，故k3,3不是平面图。
同胚的概念
定理3.5，G是平面图的充要条件
一般使用定理的下面这个形式来证明某个图不是平面图（将其收缩成K5或K3,3）
G的初等收缩概念
图的厚度估计式
扫一扫
2937
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
