【图论及其运用 — 电子科技大学】（六）第六章平面图

最新推荐文章于 2024-07-17 17:40:04 发布

青年有志

最新推荐文章于 2024-07-17 17:40:04 发布

阅读量334

点赞数 3

分类专栏：研究生课程文章标签：图论算法

本文链接：https://blog.csdn.net/qq_46450354/article/details/136993195

版权

研究生课程专栏收录该内容

21 篇文章 0 订阅

订阅专栏

一、平面图概念与性质

(一)、平面图的概念

图的平面性问题是图论典型问题之一。生活中许多问题都与该问题有关。

上面的例子都涉及同一个图论问题：能否把一个图画在平面上，使得边与边之间没有交叉？针对这一问题，我们引入如下概念

定义1 如果能把图 $G$ 画在平面上，使得除顶点外，边与边之间没有交叉，称 $G$ 可嵌入平面，或称 $G$ 是可平面图。可平面图 $G$ 的边不交叉的一种画法，称为 $G$ 的一种平面嵌入， $G$ 的平面嵌入表示的图称为平面图。

由定义，图 $G$ 的平面嵌入只是 $G$ 的一种方式，它和 $G$ 实际上是同一个图

注： (1) 可平面图概念和平面图概念有时可以等同看待；(2) 图的平面性问题主要涉及如下几个方面：1) 平面图的性质；2) 平面图的判定；3) 平面嵌入方法(平面性算法) ;4）涉及图的平面性问题的拓扑不变量。

(二)、平面图性质

定义2 (1) 一个平面图 $G$ 把平面分成若干连通片，这些连通片称为 $G$ 的区域，或 $G$ 的一个面。 $G$ 的面组成的集合用 $Φ$ 表示。（ $G$ 是一个平面图， $G$ 将所嵌入的平面划分为若干个区域，每个区域的内部连同边界称为 $G$ 的面）

(2) 面积有限的区域称为平面图 $G$ 的内部面，否则称为 $G$ 的外部面或无限面。

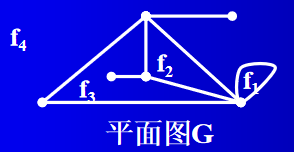
$f_1$ 是一个环围成的区域， $f_2$ 是三条边组成的三角形区域， $f_3$ 由五条边围成， $f_4$ 是无限面，面无限大的

在上图 $G$ 中，共有 $4$ 个面。其中 $f_4$ 是外部面，其余是内部面。 $Φ=\{f_1, f_2, f_3, f_4\}$ 。

在任何一个图中，均有且仅有一个无限面（外部面）

一个点组成的平面图，规定是只有一个无限面

(3) 在 $G$ 中，顶点和边都与某个给定区域关联的子图，称为该面的边界。某面 $f$ 的边界中含有的边数(割边计算2次)称为该面 $f$ 的次数, 记为 $d e g (f)$ 。

在上图中，红色边在 $G$ 中的导出子图为面 $f_3$ 的边界。 $f_1$ 是个环， $f_2$ 是三条边组成的三角形面， $f_3$ 有 4 条非割边，但是有一条割边，算两次、 $f_4$ 外部面看最外部的边界，环也是外部面的边界，还有一个割边

可以观察到，总次数是边数的二倍，总次数为 16，边数为 8，这个在所有图中都是成立的

1、平面图的次数公式

定理1 设 $G = (n, m)$ 是平面图，则：
$\sum_{f\in\Phi}\deg(f)=2m$
证明： 对 $G$ 的任意一条边 $e$ , 如果 $e$ 是某面割边，那么由面的次数定义，该边给 $G$ 的总次数贡献 $2$ 次；如果 $e$ 不是割边，那么，它必然是两个面的公共边，因此，由面的次数定义，它也给总次数贡献 $2$ 次。于是有：
$\sum_{f\in\phi}\deg(f)=2m$

实际上就是，除了割边之外的一条边会关联两个面，而割边会计算两次。所以构建 $f$ 的边的总次数，为边的两倍

2、平面图的欧拉公式

定理2(欧拉公式) 设 $G = (n, m)$ 是连通平面图， $\phi$ 是 $G$ 的面数，则：
$n-m+\phi=2$

以下是书上的证明方法：（本人觉得说明得更好些）

下面是 PPT 上证明：

证明：
情形1，如果 $G$ 是树，那么 $\phi=1$ （树只有一个外部面）。在这种情况下，容易验证，定理中的恒等式是成立的。
情形2， $G$ 不是树形的连通平面图。
假设在这种情形下，欧拉恒等式不成立。则存在一个含有最少边数的连通平面图 $G$ , 使得它不满足欧拉恒等式。设这个最少边数连通平面图 $G = (n, m)$ , 面数为 $\phi$ ，则：
$n-m+\phi\neq2$
因为 $G$ 不是树，所以存在非割边 $e$ 。显然， $G - e$ 是连通平面图，边数为 $m - 1$ , 顶点数为 $n$ , 面数为 $\phi-1$ 。
由最少性假设， $G - e$ 满足欧拉等式： $n-(m-1)+(\phi-1)=2$
化简得： $n-m+\phi\neq2$ 这是一个矛盾。
注：该定理可以采用对面数 $\phi$ 作数学归纳证明。

一个可平面图有多种平面嵌入，但无论是何种平面嵌入，由定理 2 容易知道他们的面数是相等的。

3、欧拉公式的几个有趣推论

推论1 设 $G$ 是具有 $\phi$ 个面 $k$ 个连通分支的平面图，则：
$n-m+\phi=k+1$

证明： 对第 $i (1 ≦ i ≦ k)$ 个分支来说，设顶点数为 $n_i$ ，边数为 $m_i$ ，面数为 $\phi$ , 由欧拉公式： $n_i-m_i+\phi_i=2$
所以， $\sum_{i=1}^k\left(n_i-m_i+\phi_i\right)=2k$
$\sum_{i=1}^kn_i-\sum_{i=1}^km_i+\sum_{i=1}^k\phi_i=2k$
而：
$\sum_{i=1}^kn_i=n ~~~~ \sum_{i=1}^km_i=m ~~~~ \sum_{i=1}^k\phi_i=\phi+(k-1) \text{ 这是因为外部面多计算了 (k - 1) 次}$
所以得：
$n-m+\phi=k+1$

推论2 设 $G$ 是具有 $n$ 个点 $m$ 条边 $\phi$ 个面的连通平面图，如果对 $G$ 的每个面 $f$ ,有： $d e g (f) \geq l \geq 3$ , 则：（ $l$ 可以看做是 $G$ 中的一个圈的边长，即 $d e g (f) \geq l$ 表示 $G$ 中所有圈的边长至少为 $l$ ）
$m\leq\frac l{l-2}(n-2)$

注： (1)上面推论2也可以叙述为：
设 $G = (n, m)$ 是连通图，如果： $m>\frac l{l-2}(n-2)$ 则G是非可平面图。

(2) 推论2的条件是 $G$ 是平面图的必要条件,不是充分条件。

偶图一定不存在奇圈, 所以 $K_{3,3}$ 没有长度小于 $4$ 的圈

推论3 设 $G$ 是具有 $n$ 个点 $m$ 条边 $\phi$ 个面的简单平面图，若 $n \geq 3$ ，则：（每个面的次数一定满足 $\geq 3$ ，因为至少 3 条边才能围成一个圈）
$m\leq3n-6$

推论4 设 $G$ 是具有 $n$ 个点 $m$ 条边的连通平面图，若 $G$ 的每个圈均由长度是 $l$ 的圈围成，则：
$m (l - 2) = l (n - 2)$

证明： 由次数公式，欧拉公式容易得证。将推论2中的不等式改为等式即可

推论5 设 $G$ 是具有 $n$ 个点 $m$ 条边的简单平面图，则： $\delta\leq5$

定理3 一个连通平面图是 $2$ 连通的，当且仅当它的每个面的边界是圈。（了解）

2连通图中，没有环是一定没有割边的

推论6 若一个平面图是 $2$ 连通的，则它的每条边恰在两个面的边界上。（了解）

(三)、图的嵌入性问题简介（仅了解，属于扩展内容，但是是有必要了解的）

在图的平面嵌入的基础上，简单介绍：

1、曲面嵌入

1)、球面嵌入

定理4 $G$ 可球面嵌入当且仅当 $G$ 可平面嵌入。
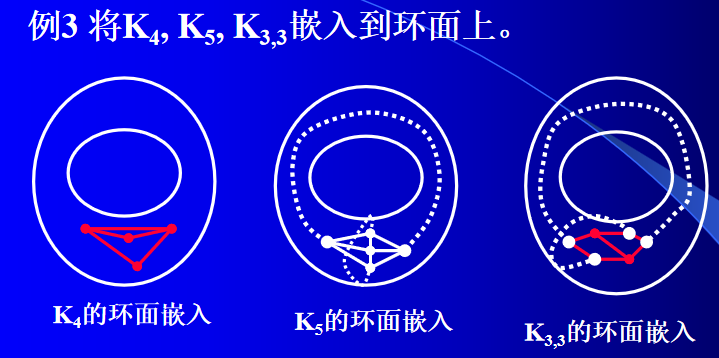
在这里插入图片描述

2)、环面嵌入
环面的形状像一个汽车轮胎的表面。
在这里插入图片描述

在这里插入图片描述

3) 定向曲面嵌入
这是目前嵌入性问题研究热点。国内：刘彦佩，黄元秋等是从事该方向研究的代表。

2、图的3维空间嵌入

定理5 所有图均可嵌入 $R^3$ 中。

证明： 在 $R^3$ 中作空间曲线：
$\left.l:\left\{\begin{aligned}x&=t\\y&=t^2\\z&=t^3\end{aligned}\right.\right.$

把图 $G$ 的顶点放在该直线的不同位置，则 $G$ 的任意边不相交。

事实上，对处于曲线 $l$ 上的任意 $4$ 个相异顶点，它们对应的参数值分别为： $t_1,t_2,t_3,t_4$ 。

因为：
$\begin{vmatrix}1&t_1&{t_1}^2&{t_1}^3\\1&{t_2}&{t_2}^2&{t_2}^3\\1&{t_3}&{t_3}^2&{t_3}^3\\1&{t_4}&{t_4}^2&{t_4}^3\end{vmatrix}\neq0$

所以，上面 $4$ 点不共面。

(四)、凸多面体与平面图

一个多面体称为凸多面体，如果在体上任取两点，其连线均在体上。

凸多面体的一维骨架：把一个凸多面体压缩在平面上，得到一个对应的平面图，该平面图称为该凸多面体的一维骨架。
在这里插入图片描述

定理6 存在且只存在5种正多面体：它们是正四、六、八、十二、二十面体。

证明： 任取一个正 $\phi$ 面体，其顶点数、棱数分别是 $n$ 和 $m$ 。对应的一维骨架是一个每个面次数为 $l$ ,顶点度数为 $r$ 的简单平面正则图 $G$ .

在这里插入图片描述

二、特殊平面图与平面图的对偶图

(一)、特殊平面图

1、极大平面图及其性质

对于一个简单平面图来说，在不邻接顶点对间加边，当边数增加到一定数量时，就会变成非平面图。这样，就启发我们研究平面图的极图问题。

定义1 设 $G$ 是简单可平面图，如果 $G$ 是 $K_i (1≦i≦4)$ , 或者在 $G$ 的任意非邻接顶点间添加一条边后，得到的图均是非可平面图，则称 $G$ 是极大可平面图。 极大可平面图的平面嵌入称为极大平面图。

第一个图是一个 $K_4$ 图，第二个图在任意两个顶点之间添加边，不会破坏平面性、第三个图在某些点连接后会导致边交叉

注：只有在单图前提下才能定义极大平面图。（因为如果允许存在环，则无论在每个顶点画多少个环，都不影响其平面性）

引理设 $G$ 是极大平面图，则 $G$ 必然连通；且若 $G$ 的阶数大于等于 $3$ （ $n \geq 3$ ），则 $G$ 无割边。

下面证明极大平面图的一个重要性质。

定理1 设 $G$ 是至少有 $3$ 个顶点的平面图，则 $G$ 是极大平面图，当且仅当 $G$ 的每个面的次数是 $3$ 且为单图。

注：该定理可以简单记为是“极大平面图的三角形特征”，即每个面的边界是三角形。

注意： 为什么构造的 $f$ 不能再内部添加边，就是因为我们需要保证 $f$ 的次数大于等于 4，从而说明矛盾，从而必须在 $f$ 内部添加边才行。

围绕极大性进行证明

推论： 设 $G$ 是 $n$ 个点， $m$ 条边和 $\phi$ 个面的极大平面图，且 $n \geq 3$ .则：
(1) $m = 3 n - 6$ ;
(2) $\phi=2n-4$ .

注：顶点数相同的极大平面图并不唯一。例如：

还在研究中的问题是：顶点数相同的极大平面图的个数和结构问题。

定义2 如果在不可平面图 $G$ 中任意删去一条边所得的图为可平面图，则称 $G$ 为极小不可平面图。

例如 $K_5$ 与 $K_{3,3}$ 均为极小不可平面图

2、极大外平面图及其性质

定义3 若一个可平面图 $G$ 存在一种平面嵌入，使得其所有顶点均在某个面的边界上，称该图为 外可平面图。外可平面图的一种外平面嵌入，称为外平面图。

为什么第一个图是外可平面图呢，是因为可以同构出将所有点均在同一个平面上，如外平面图1和外平面图2，所有点均在同一面 $f$ 上 （实际上可以看成，是否可以把所有顶点排布在外平面的边界上）

注：对外可平面图 $G$ 来说，一定存在一种外平面嵌入，使得 $G$ 的顶点均在外部面的边界上 （如上图的外平面图2）。这由球极投影法可以说明。

下面研究极大外平面图的性质。

定义4 设 $G$ 是一个简单外可平面图，若在 $G$ 中任意不邻接顶点间添上一条边后， $G$ 成为非外可平面图，则称 $G$ 是极大外可平面图。极大外可平面图的外平面嵌入，称为极大外平面图。（联系到极大图，一定都是简单图，不能有环，因为环可以无限加）

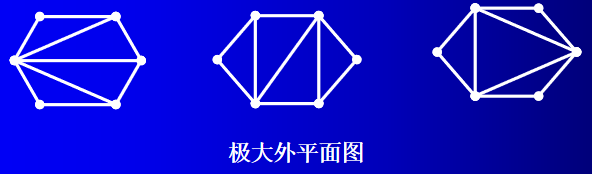
引理设 $G$ 是一个连通简单外可平面图，则在 $G$ 中存在度数至多是2的顶点。(证明略)

定理2 设 $G$ 是一个有 $n (n \geq 3)$ 个点，且所有点均在外部面上的极大外平面图，则 $G$ 有 $n - 2$ 个内部面。（考过这道题）

$G$ 是极大外平面， $G_1$ 只是 $G$ 去掉了外平面上的一个 2 度点，依然满足其他所有点在外部面上， $G_1$ 是极大外平面图，把这个点现在加回来，则多一条边，则面数 $k - 2 + 1$ 也即，内部面为 $(k + 1) - 2$ ，因为 $G$ 有 $k + 1$ 个点

定理3 设 $G$ 是一个有 $n (n \geq 3)$ 个点，且所有点均在外部面上的外平面图，则 $G$ 是极大外平面图，当且仅当其外部面的边界是圈，内部面是三角形。

定理4 每个至少有7个顶点的外可平面图的补图不是外可平面图，且7是这个数目的最小者。(了解即可)

我们用枚举方法证明。

(二)、平面图的对偶图

1、对偶图的定义

定义4 给定平面图 $G$ ， $G$ 的对偶图 $G^*$ 如下构造：

(1) 在 $G$ 的每个面 $f_i$ 内取一个点 $v_i^*$ 作为 $G^*$ 的一个顶点；

(2) 对 $G$ 的一条边 $e$ , 若 $e$ 是面 $f_i$ 与 $f_j$ 的公共边，则连接 $v_i^*$ 与 $v_j^*$ ，得 $G^*$ 的边 $v_i^*v_j^*$ , 且 $v_i^*v_j^*$ 与 $e$ 相交；若 $e$ 是面 $f_i$ 中的割边（若 $e$ 只在一个面 $f_i$ 上时），则以 $v_i^*$ 为顶点作环，得 $G^*$ 的边 $v_i^*v_i^*$ ，且让它与 $e$ 相交。（相当于考虑原图的每个边，如果这条边在两个面上，则连接这两个面，如果这个边仅在一个面上，则形成环，仅在一个面上的边通常是割边）

2、对偶图的性质

(1)、 $G$ 与 $G^*$ 的对应关系

$G^*$ 的顶点数等于 $G$ 的面数；
$G^*$ 的边数等于 $G$ 的边数；（因为每条边都考虑了在 $G^*$ 中与之对应的每条边）
$G^*$ 的面数等于 $G$ 的顶点数；
$d (v^*)=deg( f )$

(2)、定理5
定理5 平面图 $G$ 的对偶图必然连通

(2) $G$ 是平面图，则 $(G^*)^*\cong G$ 当且仅当 $G$ 是连通的。(习题第26题)

在这里插入图片描述

(3) 同构的平面图可以有不同构的对偶图。
在这里插入图片描述

第二次上交作业
第4章习题4 ：3，7，10，12.
第5章习题5 ：1，2，6，7，13，19。

三、平面图的判定与涉及平面性的不变量

(一)、平面图的判定

回顾：已经学过的判定

在本章第一次课中，我们已经明确：对于 $3$ 阶以上的具有 $m$ 条边的单图 $G$ 来说，如果 $G$ 满足如下条件之一： (1) $m > 3 n - 6$ ; (2) $K_5$ 是 $G$ 的一个子图；(3) $K_{3,3}$ 是 $G$ 的一个子图，那么， $G$ 是非可平面图。

$K_5$ 和 $K_{3,3}$ 均不是可平面图，这两个图被称为基本非平面图或Kuratowaki图

但上面的条件仅为 $G$ 是非可平面图的充分条件。

这次课要解决的问题是：给出判定一个图是否是可平面图的充分必要条件。

最早给出图的平面性判定充要条件的是波兰数学家库拉托斯基(30年代给出)。后来，美国数学家惠特尼，加拿大数学家托特，我国数学家吴文俊等都给出了不同的充要条件。

我们主要介绍波兰数学家库拉托斯基的结果。

1、相关概念

定义1 在图 $G$ 的边上插入一个新的 $2$ 度顶点，使一条边分成两条边，称将图在 $2$ 度顶点内扩充；去掉一个图的 $2$ 度顶点，使关联它们的两条边合并成一条边，称将图 $G$ 在 $2$ 度顶点内收缩。

定义2 两个图 $G_1$ 与 $G_2$ 说是同胚的，如果 $G_1\cong G_2$ ，或者通过反复在 $2$ 度顶点内扩充和收缩后能够变成一对同构的图。（或称为 $G_1$ 与 $G_2$ 在 $2$ 度顶点内是同构的，同胚的两个图点数和边数可能都不一样）

扩充和收缩不会改变这个图是否可平面，即一个图本身是可平面的，扩充 $2$ 度顶点，仍然可平面，本身不是，扩充了仍然不是可平面的。收缩同理

注：显然，图的平面性在同胚意义下不变。

定理1 (库拉托斯基定理) 图 $G$ 是可平面的，当且仅当它不含 $K_5$ 和 $K_{3,3}$ 同胚的子图。（只介绍此定理的结论与运用，证明不要求）

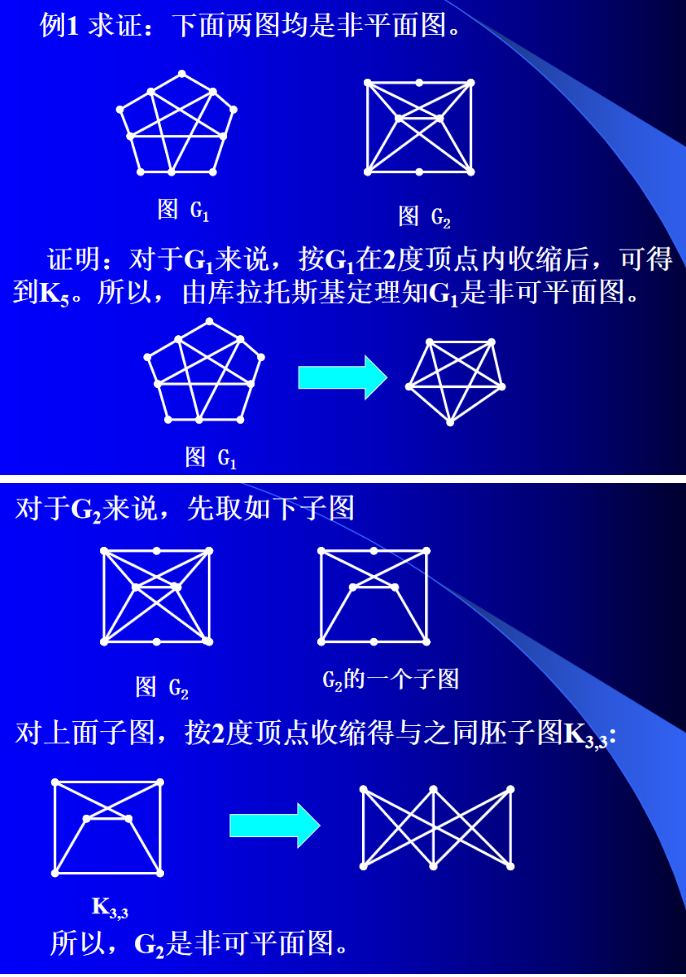
下面说不存在与 $K_5$ 同胚的子图，因为最大度为 4 的顶点才 4 个，是因为， $K_5$ 每个顶点度数为 4，共 5 个点，如何都不能通过 2 度扩张或收缩得到

定义3 给定图 $G$ , 去掉 $G$ 中的环，用单边代替平行边（重边）而得到的图称为 $G$ 的基础简单图。

定理2 (1) 图 $G$ 是可平面的，当且仅当它的基础简单图是可平面的；（实际上就是说环和重边或叫平行边并不影响其平面性）
(2) 图 $G$ 是可平面图当且仅当 $G$ 的每个块是可平面图。（没有割点的图就是一个块）

意味着如果图 $G$ 有割点，可以将图 $G$ 分为多个块，分别对块进行平面性检查

定义3 设 $uv$ 是简单图 $G$ 的一条边。去掉该边，重合其端点，再删去由此产生的环和平行边（重边）。这一过程称为图 $G$ 的初等收缩或图的边收缩运算。并记为 $G / uv$

称 $G$ 可收缩到 $H$ ,是指对 $G$ 通过一系列边收缩后可得到图 $H$ 。

定理2 (瓦格纳定理)： 简单图 $G$ 是可平面图当且仅当它不含有可收缩到 $K_5$ 或 $K_{3,3}$ 的子图。

定理3 至少有 $9$ 个顶点的简单可平面图的补图是不可平面的，而 $9$ 是这个数目中的最小的一个。(了解即可)

此题考过

(二)、涉及平面性的不变量（作为了解性内容）

我们将要讨论的问题是：如何刻画一个非可平面图与平面图之间的差距。只作简单介绍。

1、图的亏格

环柄：边交叉处建立的“立交桥”。通过它，让一条边经过 “桥下”，而另一条边经过“桥上”，从而把两条边在交叉处分开。
在这里插入图片描述

定义4 若通过加上 $k$ 个环柄可将图 $G$ 嵌入到球面，则 $k$ 的最小数目，称为 $G$ 的亏格，记为： $γ (G)$ 。

定理4 对于一个亏格为 $γ$ ，有 $n$ 个顶点， $m$ 条边和 $\phi$ 个面的多面体，有：
$n-m+\phi=2-2\gamma$

因多面体对应一个连通图，所以上面恒等式称为一般连通图的欧拉公式。

推论： 设 $G$ 是一个有 $n$ 个点 $m$ 条边，亏格为 $γ$ 的连通图，则：

(1), $\gamma\geq\frac16m-\frac12(n-2)$
(2), $\text{若 }G\text{无三角形,则 }:\quad\gamma\geq\frac14m-\frac12(n-2)$
(3), $\text{若}G\text{每个面是三角形,则:}m{=}3(n-2{+}2\gamma)$
(4), $\text{若}G\text{每个面是四边形,则: }m{=}2(n-2{+}2\gamma)$

在这里插入图片描述

对于完全图的亏格曾经是一个长期的，有趣的，困难的和成功的努力。1890年希伍德提出如下猜想：

$\gamma(K_n)=\left\{\frac{(n-3)(n-4)}{12}\right\}\cdots(*)$

希伍德由推论(1)证明了：
$\gamma(K_n)\geq\frac{(n-3)(n-4)}{12}$

同时希伍德也证明了 $γ(K_7)=1$ .

1891年，赫夫曼对n= 8—12 进行了证明；

1952年，林格尔对n= 13 进行了证明；

记阶数 $n = 12 s + r$

1954年，林格尔对 $r = 5$ 进行了证明；

1961–65年，林格尔对 $r = 7 、 10 、 3$ 进行了证明；

1961–65年，杨斯、台里等对r= 4、0、1、9、6 进行了证明；

1967–68年，林格尔、杨斯对r= 2、8、11进行了证明；

1968年后，法国蒙特派列尔大学文学教授杰恩对n=18、20、23进行了证明.

对于完全双图，结果由林格尔独立得到。

定理5 设 $m, n$ 是正整数，则：
$\gamma(K_n)=\left\{\frac{(n-3)(n-4)}{12}\right\} ~~~~~~~~~~~ \gamma(K_{m,n})=\left\{\frac{(m-3)(n-2)}4\right\}$

2、图的厚度

定义5 若图 $G$ 的 $k$ 个可平面子图的并等于 $G$ ，则称 $k$ 的最小值为 $G$ 的厚度，记为 $\theta(G)$

定理6 (1)若 $n\neq4({\mathrm{mod}}6)\text{或}n\neq9$ ,则： $\theta(K_n)=\left\lfloor\frac{n+7}6\right\rfloor$

(2) $\theta(K_{m,n})=\left\lfloor\frac{mn}{2(m+n-2)}\right\rfloor$

(3) 对任意的单图G=(n, m),有： $\theta\geq\frac m{3n-6}$

3、图的糙度

定义6 图G中边不相交的不可平面子图的最多数目称为
G的糙度，记为： $\xi(G)$

定理7 完全图的糙度由下式给出：
在这里插入图片描述

$\xi\left(K_{3n+1}\right)={\binom n2}+2{\left\lfloor\frac n3\right\rfloor}$
(3n+1≥19并且3n+1≠9r+7，其中r为面数）；

$\xi(K_{3n+2})=\binom n2+\left\lfloor\frac{14n+1}{15}\right\rfloor$

定义8 将G画在平面上时相交的边对的最少数目称为G的叉数，记为 $\text{η (G )}$

定理9
$\eta(K_n){\leq}\frac14{\left\lceil\frac n2\right\rceil}{\left\lceil\frac{n-1}2\right\rceil}{\left\lceil\frac{n-2}2\right\rceil}{\left\lceil\frac{n-3}2\right\rceil}$

$\eta(K_{m,n})\leq\left\lceil\frac m2\right\rceil\left\lceil\frac{m-1}2\right\rceil\left\lceil\frac n2\right\rceil\left\lceil\frac{n-1}2\right\rceil$

P143—146 习题5 ：6，7，8，11、12。

四、平面性算法（重点）

(一)、涉及算法的相关概念

关于图的平面性问题，我们已经建立了一些平面性判定方法：

(1) 对于简单图 $G = (n, m)$ ，如果 $m > 3 n - 6$ ，则 $G$ 是非可平面的；

(2) 对于简单连通图 $G = (n, m)$ ，如果每个面次数至少为 $l \geq 3$ ,且 $m>\frac{(n-2)l}{(l-2)}$ ，则 $G$ 是非可平面的；

(3) 库拉托斯基定理： $G$ 是可平面的当且仅当 $G$ 不含有与 $K_5$ 和 $K_{3,3}$ 同胚的子图；

(4) 瓦格纳定理： $G$ 是可平面的当且仅当 $G$ 不含有能够收缩成 $K_5$ 和 $K_{3,3}$ 的子图；

上面的判定方法，局限性很大。这次课我们将给出一个算法，其作用是：如果 $G$ 非可平面，通过算法可以得到判定；如果 $G$ 是可平面图，通过算法，可以给出一种平面嵌入形式。

定义1 设 $H$ 是 $G$ 的一个子图，在 $E (G) - E (H)$ 中定义一个二元关系 “~”:

$\forall e_1,e_2\in E(G)-E(H),e_1\thicksim e_2\text{当且仅当存在一条途径} W,\text{ 使得}:$

(1) $e_1$ 与 $e_2$ 分别是 $W$ 的始边和终边，且

(2) $W$ 与 $H$ 是内部不相交的。（即 $W$ 的内部顶点，均不是 $H$ 的顶点）

注意： 下图标出的 $e_i$ 均为白色边

如图假设红边构成图 $H$ ，全部边构成 $G$ ，则 $E (G) - E (H)$ 由图中白色边组成， $e_1e_3$ 满足条件，而 $e_1e_4$ 不满足条件。

容易验证 “~” 具有自反性，对称性和传递性，从而是 $\ E ( H ) E(G) \backslash E(H)$ 上的一个等价关系。此等价关系的等价类导出的 $G - E (H)$ 的子图称为 $H$ 中的桥。桥与 $H$ 的公共顶点称为附着顶点。 （这里的等价类用人话说就是上图中在同一二元关系里面的集合，组成一个等价类，如 $e_1, e_2, e_3$ 两两相互之间满足二元关系，所以是一个等价类。而 $e_4$ 与 $e_1, e_5$ 均不满足二元关系，所以 $e_4$ 自身是一个等价类，同理）

定义2 设 $B$ 是 $E (G) - E (H)$ 关于二元关系“ ~” 的等价类在 $G$ 中的边导出子图，则称 $B$ 是 $G$ 关于子图 $H$ 的一座桥。桥与 $H$ 的公共顶点称为桥 $B$ 在 $H$ 中的附着顶点。

如下图 $e_1, e_2, e_3$ 相互满足二元关系， $e_4$ 与自身满足二元关系， $e_5$ 与自身满足二元关系， $e_6, e_7$ 满足二元关系，所以存在四个等价类，分别为 ${e_1, e_2, e_3\}$ 、 ${e_4\}$ 、 ${e_5\}$ 、 ${e_6, e_7\}$ ，等价类的边导出子图，即为桥，所以有四个桥，而这些桥中，与 $H$ 有公共点的那些顶点，叫附着顶点。

定义3 设 $H$ 是图 $G$ 的可平面子图， $\tilde{H}$ 是 $H$ 的一种平面嵌入。若 $G$ 也是可平面图，且存在 $G$ 的一个平面嵌入 $\tilde{G}$ ，使得： $\tilde{H}\subseteq\tilde{G}$ ，称 $\tilde{H}$ 是 $G$ 容许的。

即 $G$ 中，把那条白色边拉出来如 $\tilde{G}$ 中虚白线所示，而 $\tilde{H}$ 是红线部分， $\tilde{G}$ 在 $\tilde{H}$ 的基础上多了一条白虚线，满足两个都存在平面嵌入，且 $\tilde{H}\subseteq\tilde{G}$ ，即 $\tilde{H}$ 是 $G$ 容许的。（注意 $\tilde{H}$ 定下来在判定的时候就不能变动了，边也不能拉缩，因为改动了，就不是 $\tilde{H}$ 了）

白色那条边无论怎么动，都会和红色线边交叉（注意红色线不能动，因为动了，就不是 $\tilde{H}$ 了）

定义4 设 $B$ 是 $G$ 中子图 $H$ 的任意一座桥，若 $B$ 对 $H$ 的所有附着顶点都位于 $\tilde{H}$ 的某个面 $f$ 的边界上，则称 $B$ 在面 $f$ 内可画入，否则，称 $B$ 在面 $f$ 内不可画入。

对于 $G$ 的桥 $B$ ,令： $\color{red} F(B,\tilde{H})=\left\{\left.f\right|f\text{是}\tilde{H}\text{的面,且}B\text{在}f\text{内可画入}\right\}$

红色边为 $\tilde{H}$ , $\tilde{H}$ 的面为 $f_1$ 四边形， $f_2$ 六边形，外部面 $f_3$

注意除 $\tilde{H}$ 中边以外的边才能组成桥，桥 $B_1$ 为浅蓝色边组成，桥 $B_2$ 为黄色边，桥 $B_3$ 为白色边组成

找每个桥的所有附着顶点，所有附着顶点在同一面上，则称可画入这个面，如 $B_1$ 共三个点，但只有一个附着点，这个附着顶点同时在面 $f_2, f_3$ 上，所以 $B_1$ 可画入到 $f_2, f_3$ 这两个面上，即 $F(B_1,\tilde{H})=\begin{Bmatrix}f_2,f_3\end{Bmatrix}$

$B_2$ 有三个附着顶点，其中两个在 $f_2$ 上，一个在 $f_1$ 上，但是三个点都属于 $f_3$ ，所以 $F(B_2,\tilde{H})=\begin{Bmatrix}f_3\end{Bmatrix}$

定理1 设 $\tilde{H}$ 是 $G$ 容许的，则对于 $H$ 的每座桥 $B$ ： $F(B,\tilde{H})\neq\Phi$

注：定理1实际上给出了一个图是可平面图的一个必要条件。这个必要条件表明：如果存在 $G$ 的一个可平面子图 $H$ ,使得对于某桥 $B$ ，有 $F(B,\tilde{H}){=}\Phi$ ，那么， $G$ 是非可平面的。

根据上面的结论：我们可以按如下方式来考虑 $G$ 的平面性问题：

(二)、平面性算法

1964年，德穆克龙(Demoucron), 莫尔根思(Mlgrance)和珀特维斯(Pertuiset)提出了下面的平面性算法，简称DMP算法。

说明：习题6的1----9题比较简单，要求自己独立完成。没有讲到的习题，作为参考。

P143—146 习题6 ：1----9

青年有志

关注

3
点赞
踩
6

收藏

觉得还不错? 一键收藏
0
评论
【图论及其运用 — 电子科技大学】（六）第六章平面图

定义4给定平面图GGGGGG的对偶图G∗G^*G∗如下构造：(1) 在GGG的每个面fif_ifi内取一个点vi∗v_i^*vi∗作为G∗G^*G∗的一个顶点；(2) 对GGG的一条边eee, 若eee是面fif_ifi与fjf_jfj的公共边，则连接vi∗v_i^*vi∗与vj∗v_j^*vj∗，得G∗G^*G∗的边vi∗vj∗v_i^*v_j^*vi∗。
复制链接

扫一扫