解决one-stage目标检测正负样本不均衡的另类方法--Gradient Harmonized

最新推荐文章于 2024-04-08 09:46:15 发布

叫我西瓜超人

最新推荐文章于 2024-04-08 09:46:15 发布

阅读量7.4k

点赞数 11

分类专栏：深度学习

本文链接：https://blog.csdn.net/watermelon1123/article/details/89362220

版权

深度学习专栏收录该内容

19 篇文章 2 订阅

订阅专栏

正负样本不均衡问题一直是One-stage目标检测中被大家所诟病的地方，He Keming等人提出了Focal Loss来解决这个问题。而AAAI2019上的一篇论文《Gradient Harmonized Single-stage Detector》则尝试从梯度分部的角度，来解释样本分步不均衡给目one-stage目标检测带来的瓶颈本质，并尝试提出了一种新的损失函数：GHM(Gradient Harmonizing Mechanism)来解决这个问题。

Gradient Norm

Cross Entropy Loss是分类中常用的一种损失，其表达式：

其中 $p=sigmoid(x)$ ， $p^*$ 为类别的真实标签，如果 $L_C_E$ 对 $x$ 求导，可以得到下列式子：

可以定义g为：

这里的g被定义为梯度模长gradient norm。直观表示上看，g表明了样本的真实值与当前预测值的距离。观测下图，下图是一个one-stage模型收敛后画出的梯度模长分布图。横坐标为gradient norm，纵坐标可以理解为数据分部的比例（做了log scale）。画红框的部分为easy examples，对应着横坐标有着非常低的gradient norm，可以看到easy examples的梯度模长非常小，表明了这些样本的真实值和预测值非常接近了，但是其数量所占比例非常大，其实这部分easy example对于模型的提升效果非常小。

同时注意画绿框的部分，这部分为样本中的very hard example，文中认为，这部分样本同样对模型的提升效果没有帮助，这部分样本同样也有着非常大的比例。其实我们需要关注的应该是中间部分的样本（既不是easy example也不是very hard example），这些样本对模型的提升更有帮助。

文中有提到过，GHM之所以效果更好，不仅仅因为对easy example做了loss上的抑制，同时对very hard example也起到了一定的忽略作用。文中把这些very hard examples定义为离群点outliers，这些outliers在模型的不断拟合过程中一直为very hard examples，如果模型强行的去拟合这些outliers，反而会起到适得其反的效果，这也就是为什么也要抑制这些very hard examples的原因之一。

Gradient Density

为了解决gradient norm分部不均匀的问题，文章定义了梯度密度gradient density：

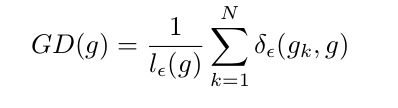
其中：

$\delta _\varepsilon (g_x,g)$ 表明了样本1～N中，梯度模长分布在 $(g-\frac{\varepsilon }{2},g+\frac{\varepsilon }{2})$ 范围内的样本个数。而 $l_\varepsilon (g)$ 代表了 $(g-\frac{\varepsilon }{2},g+\frac{\varepsilon }{2})$ 区间的长度。因此梯度密度gradient density的直观理解就是：单位梯度模长g长度内所分部的样本个数，及gradient norm的密度。

通过定义参数 $\beta _i$ :

如果定性分析一下：对于梯度密度大的样本，即 $GD\left ( g_i \right )$ 的值很大，则 $N/GD\left ( g_i \right )$ 就会相应的变小；反之对于 $GD\left ( g_i \right )$ 的值很小，则 $N/GD\left ( g_i \right )$ 就会相应的变大，而之前的分部图中可以看到，easy example和very hard example的分部都非常的密集，即GD的值很大，因此通过参数 $\beta _i$ 刚好能够达到抑制这两部分，同时提高有用样本权重的目的。

分子的N是为了使得当划分的区间长度 $\varepsilon$ 很大为1的时候 $\beta _i=1$

GHM-C Loss

通过将上面定义的 $\beta _i$ 引入cross entropy loss中，可以得到GHM-C loss的定义如下：

像上面说过的，GHM-C loss对gradient density较大的样本抑制，看下图为Cross Entropy，Focal Loss和GHM-C的对比：

GHM-C和Focal Loss都对easy example做了很好的抑制，而GHM-C和Focal Loss在对very hard examples上有更好的抑制效果。

同时因为原始定义的gadient density的计算复杂度较高，作者给出了简化版本：

其中 $ind(g)=t ,(t-1)\epsilon \leq g\leq t\epsilon$ ，

GHM-R Loss

GHM-C loss针对于分类问题，那么对于目标框的回归，作者定义了GHM-R Loss，先考虑回归中常用的smooth L1 loss：

其中 $d=(t_i-t_i^*)$ ，为输出结果和实际结果的差值。如果smooth L1对d求导，得到：

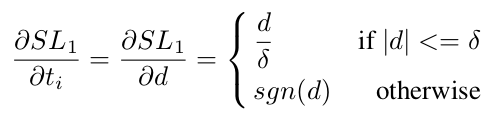
可以看到，当 $\left | d \right |\leq \delta$ 时， $d/\delta$ 可以定量的表示数据结果和真实值之间的距离；而当 $\left | d \right |\geq \delta$ 的时候，损失的梯度均为1，这样我们就无法根据梯度来估计一些example输出贡献度。基于此作者对smooth L1做了修正，得到ASL1：

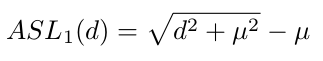
$ASL_1$ 和smooth L1具有相似的性质，并且其梯度：

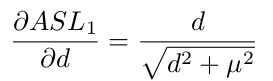
$\mu$ 是可设定超参数，论文中设定 $\mu =0.02$ 。把 $\left | d/\sqrt{d^2+\mu ^2} \right |$ 定义为gradient norm，则 $ASL_1$ 的gradient norm和样本分部的关系如下图：

通过上图可以发现有相当数量的outliers，以及outliers所对用的gradient norm值很大，因此与GHM-C相似的方式，定义GHM-R:

达到对outlier的loss达到抑制的目的。

有个值得注意的地方是在GHM-R中并没有对easy example做抑制，原文中是这样解释的：

作者认为，在目标框的回归阶段，easy examples同样能够对提升框回归的准确性带来帮助。

实验结果

因为GHM-C和GHM-R是定义的损失函数，因此可以非常方便的安插到很多目标检测方法中，作者以focal loss（我猜测应该是以RetinaNet作为baseline），对交叉熵，focal loss和GHM-C做了对比，发现GHM-C在focal loss 的基础上在AP上提升了0.2个百分点：

如果用GHM-R代替two-stage detector中的smooth L1，AP上又会有提升：

如果用上GHM-C和GHM-R，准确率的提升很明显，大概有2个百分点：

叫我西瓜超人

关注

11
点赞
踩
42

收藏

觉得还不错? 一键收藏
0
评论
解决one-stage目标检测正负样本不均衡的另类方法--Gradient Harmonized

正负样本不均衡问题一直是One-stage目标检测中被大家所诟病的地方，He Keming等人提出了Focal Loss来解决这个问题。而AAAI2019上的一篇论文《Gradient Harmonized Single-stage Detector》则尝试从梯度分部的角度，来解释样本分步不均衡给目one-stage目标检测带来的瓶颈本质，并尝试提出了一种新的损失函数：GHM(Gradient H...
复制链接

扫一扫