MOOC《人工智能：模型与算法》笔记 chapter 2

这一章主要介绍了搜索求解的相关算法。分别是启发式搜索，对抗搜索以及蒙特卡洛树搜索。

一·搜索算法：启发式搜索(有信息搜索)

在搜索的过程中利用与所求解问题相关的辅助信息，其代表算法为 贪婪最佳优 先搜索 (Greedy best-first search) 和 A* 搜索 。

下面以两个城市之间的最短距离为例介绍启发式搜索。

1.1搜索算法：贪婪最佳优先搜索

贪婪最佳优先搜索 (Greedy best-first search) ：评价函数 f(n) = 启发函数 h(n)。

从Arad节点开始，寻找与之相邻的后继节点。寻找后继节点的依据是根据Figure3.22中的数据选择

h(n)最小的节点作为后继节点，以此类推，直到扩展到Bucharest。

不难看出此方法存在一些不足之处：

1.贪婪最佳优先搜索不是最优的。经过 Sibiu 到 Fagaras 到 Bucharest 的路径比经过 Rimnicu Vilcea 到

Pitesti 到 Bucharest 的路径要长 32 公里。

2. 启发函数代价最小化这一目标会对错误的起点比较敏感。考虑从 Iasi 到 Fagaras 的问题，由启发式

建议须先扩展 Neamt ，因为其离 Fagaras 最近，但是这是一条存在死循环路径 。

3.贪婪最佳优先搜索也是不完备的。所谓不完备即它可能沿着一条无限的路径走下去而不回来做其他的选择尝试，因此无法找到最佳路径这一答案。

4.在最坏的情况下，贪婪最佳优先搜索的时间复杂度和空间复杂度都是O( )，其中𝑏是节点的分支因子数目、𝑚是搜索空间的最大深度。

因此，需要设计一个良好的启发函数。于是就有了A* 算法 。

1.2 搜索算法：A*算法

定义评价函数： f(𝑛) =                                g(𝑛)                   +               ℎ(𝑛)

                    评估函数                       当前最小开销代价              后续最小开销代价

g(𝑛)表示从起始节点到节点𝑛的开销代价值，ℎ(𝑛)表示从节点𝑛 到目标节点路径 中所估算的最小开销代价值。 f(𝑛)可视为经过节点𝑛 、具有最小开销代价值的路径。

A* 算法保持最优的条件：启发函数具有可容性 (admissible) 和一致性 (consistency) 。

1. 将直线距离作为启发函数 ℎ(𝑛) ，则启发函数一定是可容的，因为其不会高估开销代价。

2.𝑔(𝑛)是从起始节点到节点 𝑛 的实际代价开销，且 𝑓(𝑛) = 𝑔(𝑛) + ℎ(𝑛) ，因此 𝑓(𝑛) 不会高估经过节点𝑛 路径的实际开销。

3.ℎ(𝑛)≤ 𝑐(𝑛, 𝑎, 𝑛 ′)  + ℎ(𝑛 ′ ) 构成了三角不等式。这里节点 𝑛 、节点 𝑛 ′ 和目标结点 𝐺 𝑛 之间组成了一个三角形。如果存在一条经过节点𝑛 ′ ，从节点 𝑛 到目标结点 𝐺 𝑛 的路径，其代价开销小于ℎ(𝑛) ，则破坏了 ℎ(𝑛) 是从节点 𝑛 到目标结点 𝐺 𝑛 所形成的具有最小开销代价的路径这一定义。

4.Tree-search的A*算法中，如果启发函数ℎ(𝑛)是可容的，则A*算法是 最优的和完备的；在Graph-search的A*算法中，如果启发函数ℎ(𝑛)是一致的，A*算法是最优的。

5. 如果函数满足一致性条件，则一定满足可容条件；反之不然。

6.  直线最短距离函数既是可容的，也是一致的。

7.如果ℎ(𝑛)是一致的（单调的），那么𝑓(𝑛) 一定是非递减的(non-decreasing)。

二·搜索算法：对抗搜索

对抗搜索 (Adversarial Search) 也称为博弈搜索 (Game Search)。在一个竞争的环境中，智能体(agents) 之间通过竞争实现相反的利益，一方 最大化。

2.1最小最大搜索(Minimax Search)

最小最大搜索是在对抗搜索中最为基本的一种让玩家来计算最优策略的方法。

两人对决游戏 (MAX and MIN, MAX 先走 ) 可转换为对抗搜索问题。给定一个游戏搜索树，minimax算法通过每个节点的minimax值来决定最优策略。当然，MAX希望最大化minimax值，而MIN则相反。

通过 minimax 算法，我们知道，对于 MAX 而言采取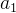行动是最佳选择，因为这能够得到最大minimax值（收益最大）。

时间复杂度：  O( )

空间复杂度  O( b × 𝑚 )

m 是游戏树的最大深度，在每个节点存在 b 个有效走法

优点:

1.算法是一种简单有效的对抗搜索手段

2.在对手也“尽力而为”前提下，算法可返回最优结果

缺点:

如果搜索树极大，则无法在有效时间内返回结果

改善:

1.使用alpha-beta pruning算法来减少搜索节点

2.对节点进行采样、而非逐一搜索 

2.2Alpha-Beta 剪枝搜索:

在极小化极大算法（ minimax 算法）中减少所搜索的搜索树节点数。该算法和极小化极大算法所得结论相同，但剪去了不影响最终结果的搜索分枝。

Alpha-Beta 剪枝搜索的性质:

• 剪枝本身不影响算法输出结果

• 节点先后次序会影响剪枝效率

• 如果节点次序“恰到好处”， Alpha-Beta 剪枝的时间复杂度为 O() ，最小最大搜索的时间复杂度为 O()

三·搜索算法：蒙特卡洛树搜索

3.1单一状态蒙特卡洛规划： 多臂赌博机 (multi-armed bandits)

单一状态， 𝑘 种行动（即有 𝑘 个摇臂）。在摇臂赌博机问题中，每次以随机采样形式采取一种行动𝑎 , 好比随机拉动第𝑘 个赌博机的臂膀，得到𝑅(𝑠, 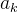) 的回报。问题：下一次需要拉动那个赌博机的臂膀，才能获得最大回报呢？

多臂赌博机问题是一种序列决策问题，这种问题需要在利用 (exploitation) 和探索 ( exploration ) 之间保持平衡。

利用 ：保证在过去决策中得到最佳回报。

探索 ：寄希望在未来能够得到更大回报。

3.2上限置信区间 (Upper Confidence Bound, UCB)

3.3蒙特卡洛树搜索

将上限置信区间算法 UCB 应用于游戏树的搜索方法，由 Kocsis 和 Szepesvari 在 2006 年提出。包括了四个步骤：选举(selection) ，扩展 (expansion) ，模拟 (simulation) ，反向传播 (Back Propagation)

  扩展 ： 如果 L 不是一个终止节点，则随机创建其后的一个未被访问节点，选择该节点作为后续子节点C。

模拟： 从节点 C 出发，对游戏进行模拟，直到博弈游戏结束。

反向传播:  用模拟所得结果来回溯更新导致这个结果的每个节点中获胜次数和访问次数。

两种策略学习机制：

搜索树策略 : 从已有的搜索树中选择或创建一个叶子结点（即蒙特卡洛中选择和拓展两个步骤）。 搜索树策略需要在利用和探索之间保持平衡。

模拟策略： 从非叶子结点出发模拟游戏，得到游戏仿真结果。

使用蒙特卡洛树搜索的原因

Monte-Carlo Tree Search (MCTS) ：蒙特卡洛树搜索基于采样来得到结果、而非穷尽式枚举（虽然在枚举过程中也可剪掉若干不影响结果的分支）。