MOOC《人工智能：模型与算法》笔记 chapter 3

逻辑与推理是人工智能的核心问题。这一章主要介绍了逻辑与推理的相关内容，分别从命题逻辑，谓词逻辑，知识图谱推理这三个方面来介绍。

一·命题逻辑

命题逻辑 (Propositional Logic) 是应用一套形式化规则对以符号表 示的描述性陈述进行推理的系统。 在命题逻辑中，一个或真或假的描述性陈述被称为原子命题，对原子命题的内部结构不做任何解析。若干原子命题可通过逻辑运算符来构成复合命题。

逻辑等价： 给定命题 𝑝 和命题 𝑞 ，如果 𝑝 和 𝑞 在所有情况下都具有同样真假结果，那么𝑝 和 𝑞 在逻辑上等价，一般用 ≡ 来表示，即 𝑝 ≡ 𝑞 。

逻辑等价为命题进行形式转换带来了可能，基于这些转换不再需要逐一列出𝑝和 𝑞 的真值表来判断两者是否在逻辑上等价，而是可直接根据已有逻辑等价公式来判断𝑝 和 𝑞 在逻辑上是否等价。

（对于命题 𝛼，若为真，则¬ 𝛼为假。𝛼，¬ 𝛼不可能同时为真或假）

命题范式

有限个简单合取式构成的析取式称为 析取范式

由有限个简单析取式构成的合取式称为 合取范式

析取范式与合取范式统称为 范式 (normal form)

假设 𝛼 𝑖 (𝑖 = 1,2, … , 𝑘) 为简单的合取式，则 𝛼 = 𝛼 1 ∨ 𝛼 2 ∨ ⋯ ∨ 𝛼 𝑘 为析取范式

例如： (¬ 𝛼 1 ∧ 𝛼 2 ) ∨ 𝛼 3 , ¬ 𝛼 1 ∨ 𝛼 3 ∨ 𝛼 2 等

假设 𝛼 𝑖 (𝑖 = 1,2, … , 𝑘) 为简单的析取式，则 𝛼 = 𝛼 1 ∧ 𝛼 2 ∧ ⋯ ∧ 𝛼 𝑘 为合取范式

例如： (𝛼 1 ∨ 𝛼 2 ) ∧ ¬𝛼 3 , ¬ 𝛼 1 ∧ 𝛼 3 ∧ ¬𝛼 2 ∨ 𝛼 4 等

一个析取范式是不成立的，当且仅当它的每个简单合取式都不成立。

一个合取范式是成立的，当且仅当它的每个简单析取式都是成立的。

任一命题公式都存在着与之等值的析取范式与合取范式 ( 注意：命题公式的析取范式与合取范式都不是唯一的)

        问题：求¬( α → 𝛽) ∨ ¬𝛾 的析取范式与合取范式

¬ ( α → 𝛽 )∨ ¬𝛾

⟺ ¬ (¬ α ∨ 𝛽 )∨ ¬𝛾

⟺ ( α ∧ ¬𝛽) ∨ ¬𝛾 析取范式

⟺ ( α ∨ ¬𝛾 )∧ (¬𝛽 ∨ ¬𝛾) 合取范式

二·谓词逻辑

命题逻辑的局限性

在命题逻辑中，每个陈述句是最基本的单位 ( 即原子命题) ，无法对原子命题进行分解。因此在命题逻辑中，不能表达局部与整体、一般与个别的关系。

例如，对于苏格拉底论断，虽知其正确的，但无法通过命题逻辑来进行推理判断：

𝛼：所有的人总是要死的

𝛽 ：苏格拉底是人

𝛾 ：所以苏格拉底是要死的

𝛼 ∧ 𝛽 → 𝛾 （不是命题逻辑的有效推理） 无法在命题逻辑基础上完成这样的推导

解决思路：

不同原子命题蕴含个体、群体和关系等内在丰富语义，命题逻辑无法表现内在丰富语义。因此，需要分析原子命题，分离其主语（个体或群体）和谓语（关系）。

需要引入更加强大的逻辑表示方法，这就是谓词逻辑

谓词逻辑

在谓词逻辑中，将原子命题进一步细化，分解出个体、谓词和量词，来表达个体与总体的内在联系和数量关系，这就是谓词逻辑研究内容。

谓词逻辑中三个核心概念： 个体、谓词（predicate ）和量词（ quantifier ）

谓词逻辑：谓词与个体

𝑃(𝑥) 表示：𝑥 <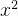

𝑃是谓词， 𝑥是个体词， 𝑥 被称为变量。 𝑥 的具体取值叫个体常项。比如，𝑃(0.1) 和 𝑃(0.02) 使得谓词为假。个体的取值范围为个体域。

一般用大写字母 𝑃,𝑄, 𝑅 等来表示谓词。上述 𝑃(𝑥) 描述了是否存在一个数，这个数小于自身平方这种关系。

谓词中可以有若干个个体变量，如 father(𝑥, 𝑦) 表示 𝑥 是 𝑦 父亲。

𝑃(𝑥) 是一元谓词（包含一个个体）， 𝑃(𝑥 1 , 𝑥 2 , … , 𝑥 𝑛 ) 被称为 𝑛 元谓词（包含若干个体）。

谓词逻辑：量词

全称量词 (universal quantifier, ∀ )

全称量词用符号 ∀ 表示，表示一切的、凡是的、所有的、每一个等。 ∀𝑥 表示定义域中的所有个体， ∀𝑥𝑃(𝑥) 表示定义域中的所有个体具有性质 𝑃 。

谓词 𝑃(𝑥) ： 𝑥 能够制造工具 。 ∀𝑥𝑃(𝑥) 表示定义域中的所有个体能够制造工具。 𝑃( 小王 ) 表示小王能够制造工具。

存在量词 (existential quantifier, ∃ )

存在量词用符号 ∃ 表示，表示存在、有一个、某些等。 ∃𝑥 表示定义域中存在一个或若干个个体， ∃𝑥𝑃(𝑥) 表示定义域中存在一个个体或若干个体具有性质 𝑃 。

谓词 𝑃(𝑥) ： 𝑥 能够制造工具。 ∃𝑥𝑃(𝑥) 表示定义域中的存在某个/某些个体能够制造工具。 𝑃( 小王 ) 表示小王能够制造工具（该命题或者为真、或者为假）。

全称量词和存在量词统称为量词。

全称量词与存在量词之间的组合

∀𝑥¬𝑃(𝑥) ≡ ¬∃𝑥𝑃(𝑥)  定义域中任意个体x不具有性质P=不存在x具有性质P    

¬∀𝑥𝑃(𝑥) ≡ ∃𝑥¬𝑃(𝑥)  定义域中不是任意个体x都具有性质P=存在x不具有性质P 

∀𝑥𝑃(𝑥)≡ ¬∃𝑥¬𝑃(𝑥)   定义域中任意个体x具有性质P=不存在x不具有性质P 

∃𝑥𝑃(𝑥) ≡ ¬∀𝑥¬𝑃(𝑥)  定义域中存在个体x具有性质P=不存在任意个体x都不具有性质P

函数与谓词的区别

函词中个体变元用个体常量（来自定义域）代入后结果仍是 个体（值域） ，如定义函数 𝑓(𝑥) = 𝑥 + 10 ，则 𝑓(2) = 12

谓词中个体变元用个体常量带入后就变成了 命题 ，如 𝑐𝑎𝑟(𝑥)。(𝑥 是车 ) 这个谓词中 𝑥 用吉普车代替，则 𝑐𝑎𝑟（ 吉普车）是命题。

  函数是从定义域到值域的映射；谓词是从定义域到{𝑇𝑟𝑢𝑒, 𝐹𝑎𝑙𝑠𝑒} 的映射

谓词演算的合式公式

命题常项、命题变项、原子谓词（不存在任何量词与联结词）是合式公式。

如果 𝐴 和 𝐵 是合式公式，那么 ¬𝐴 、 𝐴 ∧ 𝐵 、 𝐴 ∨ 𝐵 、 𝐴 → 𝐵 、 𝐴 ⟷ 𝐵 都是合式公式

如果 𝐴 是合式公式， 𝑥 是个体变元，则 ∃𝑥𝐴(𝑥) 和∀𝑥𝐴(𝑥)也是合式公式

有限次地使用上述规则求得公式是合式公式

若干谓词逻辑的推理规则

全称量词消去 (Universal Instantiation, UI) : (∀𝑥)𝐴(𝑥) → 𝐴(𝑦)

全称量词引入(Universal Generalization, UG): 𝐴(𝑦)→ (∀𝑥)𝐴(𝑥)

存在量词消去 (Existential Instantiation, EI): (∃𝑥)𝐴(𝑥) → 𝐴(𝑐)

存在量词引入 (Existential Generalization, EG): 𝐴(c) → (∃𝑥)𝐴(𝑥)

自然语言的形式化

每一个奇数均存在一个大于它的奇数：

odd(𝑥)  : 𝑥 是奇数

Great(x, y) : 𝑥 大于 𝑦

(∀𝑥)(𝑜𝑑𝑑(𝑥)→ (∃𝑦)(𝑜𝑑𝑑(𝑦)∧ 𝐺𝑟𝑒𝑎𝑡(𝑦, 𝑥)))

三·知识图谱推理

3.1知识图谱：基本概念

3.2知识图谱的构成

由于三峡大坝和葛洲坝都位于长江流域，它们之间具有反调节关系。而大古力水坝和达拉斯水坝都位于哥伦比亚河，所以推断它们之间也具有反调节关系。

学习概念或实体属性描述及其关联关系是丰富知识图谱的关键！

3.3知识图谱推理

归纳学习

归纳逻辑程序设计 (inductive logic programming ， ILP) 算法是机器学习和逻辑程序设计交叉领域的研究内容。ILP使用一阶谓词逻辑进行知识表示，通过修改和扩充逻辑表达式对现有知识归纳，完成推理任务。作为ILP 的代表性方法，一阶归纳学习 FOIL （ First Order Inductive Learner ）通过 序贯覆盖 实现规则推理。

背景知识：知识图谱中目标谓词以外的其他谓词实例化结果，如𝑆𝑖𝑏𝑙𝑖𝑛𝑔 (Ann, Mike)

推理思路：从一般到特殊，逐步给目标谓词添加前提约束谓词，直到所构成的推理规 则不覆盖任何反例。

从一般到特殊 ： 对目标谓词或前提约束谓词中的变量赋予具体值 ， 如将 (∀𝑥)(∀𝑦)(∀𝑧) (𝑀𝑜𝑡ℎ𝑒𝑟(𝑧, 𝑦)∧ 𝐶𝑜𝑢𝑝𝑙𝑒(𝑥, 𝑧)→ 𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦))这一推理规则所包含的目标谓词𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦) 中 𝑥 和 𝑦 分别赋值为 David 和 Ann ，进而进行推理。

推理过程

1.将 𝑀𝑜𝑡ℎ𝑒𝑟(𝑥, 𝑦)作为前提约束谓词加入，可得到推理规则𝑀𝑜𝑡ℎ𝑒𝑟(𝑥, 𝑦)→ 𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦)，

2.在背景知识中， 𝑀𝑜𝑡ℎ𝑒𝑟(𝑥, 𝑦) 有两个实例 :𝑀𝑜𝑡ℎ𝑒𝑟(James, Ann) ,𝑀𝑜𝑡ℎ𝑒𝑟(James, Mike)

3.对于 𝑀𝑜𝑡ℎ𝑒𝑟 (James, Ann) 这一实例， x = James ， y = Ann ，将 𝑥 和 𝑦 代入𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦)得到 𝐹𝑎𝑡ℎ𝑒𝑟 (James, Ann)，可知在训练样本中𝐹𝑎𝑡ℎ𝑒𝑟(James, Ann) 是一个反例

对于 𝑀𝑜𝑡ℎ𝑒𝑟 (James, Mike) 这一实例， x= James ， y = Mike ，将 𝑥 和 𝑦代入𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦)得到𝐹𝑎𝑡ℎ𝑒𝑟(James, Mike)，可知在训练样本中𝐹𝑎𝑡ℎ𝑒𝑟 (James, Mike) 是一个反例

4.𝑀𝑜𝑡ℎ𝑒𝑟(𝑥, 𝑦)→ 𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦)覆盖正例和反例数量分别为0和2，即𝑚 + = 0，𝑚 − = 2,

由于 𝑚 + = 0 ，代入 𝐹𝑂𝐼𝐿_𝐺𝑎𝑖𝑛 公式时会出现负无穷的情况，此时𝐹𝑂𝐼𝐿_𝐺𝑎𝑖𝑛 记为 NA （ Not Available ）

5.如果将𝐶𝑜𝑢𝑝𝑙e(𝑥, 𝑧)作为前提约束谓词加入，可得到如下推理规则𝐶𝑜𝑢𝑝𝑙e(𝑥, 𝑧) → 𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦),在背景知识中，𝐶𝑜𝑢𝑝𝑙e(𝑥, 𝑧)只有一个实例𝐶𝑜𝑢𝑝𝑙e(David, James)，即𝑥=David，𝑧= James，将其代入 𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦)得到𝐹𝑎𝑡ℎ𝑒𝑟(David, 𝑦)。

6.在训练样本中存在正例 𝐹𝑎𝑡ℎ𝑒𝑟 (David,Mike)以及反例¬𝐹𝑎𝑡ℎ𝑒𝑟(David, James)，即𝐶𝑜𝑢𝑝𝑙e(𝑥, 𝑧) → 𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦)覆盖正例和反例数量分别为1和1。信息增益值为：

𝐶𝑜𝑢𝑝𝑙e(𝑥, 𝑧) 加入后信息增益最大。将 𝐶𝑜𝑢𝑝𝑙e(𝑥, 𝑧) 加入推理规则 , 得到 𝐶𝑜𝑢𝑝𝑙𝑒(𝑥, 𝑧)→ 𝐹𝑎𝑡ℎ𝑒𝑟(𝑥, 𝑦)新推理规则。 将训练样例中与该推理规则不符的样例去掉。这里不符指当𝐶𝑜𝑢𝑝𝑙𝑒(𝑥, 𝑧) 中 𝑥 取值为 David 时，与𝐹𝑎𝑡ℎ𝑒𝑟 (David, ) 或 ¬𝐹𝑎𝑡ℎ𝑒𝑟 (David, ) 无法匹配的实例。所以此时训练样本集中只有正例𝐹𝑎𝑡ℎ𝑒𝑟 (David, Mike) 和负例¬𝐹𝑎𝑡ℎ𝑒𝑟 (David, James) 两个实例。

𝑀𝑜𝑡ℎ𝑒𝑟(𝑧, 𝑦) 加入信息增益最大。将𝑀𝑜𝑡ℎ𝑒𝑟(𝑧, 𝑦) 加入，得到新推理规则 𝑴𝒐𝒕𝒉𝒆𝒓(𝒛, 𝒚)∧ 𝑪𝒐𝒖𝒑𝒍𝒆(𝒙, 𝒛)→ 𝑭𝒂𝒕𝒉𝒆𝒓(𝒙, 𝒚) 当x= David 、 y =Mike 、 z = James 时，该推理规则覆盖训练样本集合中正例𝐹𝑎𝑡ℎ𝑒𝑟 (David, Mike) 且不覆盖任意反例，因此算法学习结束。

给定目标谓词， FOIL 算法从实例（正例、反例、背景样例）出发，不断测试所得到推理规则是否还包含反例，一旦不包含负例，则学习结束，展示了 “ 归纳学习 ”能力。