西瓜书习题 - 7.贝叶斯分类器

1.贝叶斯决策论

1、下列说法正确的是（）

1. 贝叶斯决策论是概率框架下实施决策的基本理论
2. $R(c_i|x)$表示把样本 x 分到第 i 类面临的风险
3. 如果概率都能拿到真实值，那么根据贝叶斯判定准则做出的决策是理论上最好的决策
4. 以上都正确

2、以下哪个选项是对贝叶斯最优分类器的描述？

1. 对每个样本 x 选择能使后验概率 $P(c|x)$ 最大的类别标记
2. 对每个样本 x 选择能使后验概率 $P(c|x)$ 最小的类别标记
3. 对每个样本 x 选择能使条件风险 $R(c_i|x)$ 最大的类别标记
4. 对每个样本 x 选择能使条件风险 $R(c_i|x)$ 最小的类别标记

本题选D。贝叶斯决策论(Bayesian decision theory)是概率框架下实施决策的基本方法。对分类任务来说，在所有相关概率都已知的理想情形下，贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。基于后验概率P(ci | x)可获得将样本x分类为ci所产生的期望损失(expected loss),（决策论中将“期望损失”称为“风险”(risk)）即在样本x上的"条件风险” (conditional risk)。我们的目的是寻找一个判定准则h以最小化总体风险。显然，对每个样本x，若h能最小化条件风险R(h(x) | x),则总体风险R(h)也将被最小化。这就产生了贝叶斯判定准则(Bayes decision rule):为最小化总体风险，只需在每个样本上选择那个能使条件风险R（c|x）最小的类别标记，故本题应该选D

3、$-R(h^{\ast })$反映了分类器所能达到的最____（好/坏）性能

好

本题填好。注意到贝叶斯判定准则(Bayes decision rule)为最小化总体风险，故1 - R(h*)为总体减去这个风险，所以也就是保守地能达到的好的部分；即反映了分类器能达到的最好性能。

2.生成式和判别式模型

1、决策树属于什么模型？

1. 判别式
2. 生成式
3. 判别式和生成式
4. 以上都不对

2、先对联合概率分布建模 $P(x,c)$ ，再由此获得 $P(c|x)$ ，属于什么模型？

1. 判别式
2. 生成式
3. 回归
4. 以上都不是

3、机器学习估计后验概率分为两种基本策略，____式模型和生成式模型

判别

本题填判别。监督学习模型可分为生成模型与判别模型，其分别对应着两种计算后验概率的方式。判别模型直接学习决策函数或者条件概率分布。直观来说，判别模型学习的是类别之间的最优分隔面，反映的是不同类数据之间的差异。而生成模型学习的是联合概率分布P(X,Y)，然后根据条件概率公式计算 P(Y|X)。

3.贝叶斯分类器和贝叶斯学习

1、贝叶斯主义认为，分布的参数是什么？

1. 点
2. 分布
3. 点同时也是分布
4. 以上都不对

本题选B。贝叶斯统计是基于贝叶斯理论所提供的一种对概率的解释。贝叶斯统计认为所有的参数应当使用分布来描述，而先验分布是人们主观认识的刻画。一般来说，事件发生的结果采用似然描述，而事件发生的概率分布是我们关系的后验分布，而人们对这个事件发生概率的主观认识是先验。故本题应该选B。

2、统计学习属于什么主义？

1. 频率主义
2. 贝叶斯主义
3. 两者都是
4. 两者都不是

3、贝叶斯学习____（等于/不等于）贝叶斯分类器

不等于

4.极大似然估计

1、极大似然中，若直接连乘，易造成什么现象？

1. 下溢
2. 上溢
3. 内存不足
4. 计算开销大

2、对数似然中，一般对概率取对数，然后进行以下哪个的操作？

1. 求差
2. 求和
3. 求积
4. 以上都不是

3、极大似然估计____（需要/不需要）假设某种概率分布形式

需要

本题填需要。极大似然估计，是一种概率论在统计学的应用，它是参数估计的方法之一。 说的是已知某个随机样本满足某种概率分布 ，但是其中具体的参数不清楚， 参数估计 就是通过若干次试验，观察其结果，利用结果推出参数的大概值。若一开始分布都不确定，则需要使用其他方法先确定分布，如假设检验等等。

5.朴素贝叶斯分类器

1、贝叶斯公式中，估计后验概率 P(c|x) 的主要困难在于估计以下哪个选项？

1. p©
2. p(x|c)
3. 以上两者都是
4. 以上两者都不是

本题选B。基于贝叶斯公式来估计后验概率P(c|x)主要困难在于类条件概率P(x|c)是所有属性上的联合概率，难以从有限的训练样本直接估计而得。基于有限训练样本直接计算联合概率，在计算上将会遭遇组合爆炸问题；在数据上将会遭遇样本稀疏问题；属性越多，问题越严重。为了避开这个障碍，朴素贝叶斯分类器采用了“属性条件独立性假设”：对已知类别，假设所有属性相互独立。换言之，假设每个属性独立的对分类结果发生影响相互独立。

2、朴素贝叶斯分类器中，对给定类别，模型对所有属性间的独立性有何种假设？

1. 部分不独立
2. 部分独立
3. 相互不独立
4. 相互独立

3、对____（离散/连续）属性，计算条件概率 $P(x_i|c)$ 可考虑概率密度函数

连续

本题填连续。只有连续随机变量才有概率密度函数。

6.章节测试

1、贝叶斯最优分类器____（达到了/没达到）了贝叶斯风险。

达到了

本题填达到了。回顾贝叶斯最优分类器的定义，对每个样本x，若h能最小化条件风险R(h(x) | x),则总体风险R(h)也将被最小化。这就产生了贝叶斯判定准则(Bayes decision rule):为最小化总体风险，只需在每个样本上选择那个能使条件风险R（c|x）最小的类别标记，此时, h*(x)称为贝叶斯最优分类器(Bayes optimal classifier),与之对应的总体风险R(h*)称为贝叶斯风险(Bayes risk)。根据定义，我们知道贝叶斯最优分类器就是达到贝叶斯风险的分类器。

2、在贝叶斯决策论中，下列说法错误的是（）

1. $1-R(h^{\ast })$反映了机器学习所能产生的模型精度理论上限
2. 贝叶斯最优分类器在每个样本上选择那个能使条件风险 R(c|x) 最小的类别标记
3. 在实际中，贝叶斯决策论中的$P(c_i|x)$是容易事先知道的
4. 贝叶斯最优分类器对应的总体风险称为贝叶斯风险

本题选C。从贝叶斯决策论的角度来看机器学习，我们要做的事就是去估计后验概率P(ci|x)，这自然不是一件容易的事。再看其他选项：A选项注意到贝叶斯判定准则(Bayes decision rule)为最小化总体风险，故1-R(h*)为总体减去这个风险，所以也就是保守地能达到的好的部分；即反映了分类器能达到的最好性能。B选项是最优分类器的定义。D选项是贝叶斯风险的定义。

3、从贝叶斯决策论的角度看，机器学习要实现的是基于有限的训练样本尽可能准确地估计出后验概率P(c|x) ，这句话是____（正确/错误）

正确

4、下列说法错误的是（）

1. 生成式模型可以理解为在尝试还原数据原来的联合分布
2. SVM是判别式模型
3. 判别式模型直接对后验概率建模
4. 贝叶斯分类器是判别式模型

本题选D。贝叶斯分类器是典型的生成式模型的例子。判别式模型根据训练数据得到分类函数和分界面，比如说根据SVM模型得到一个分界面，然后直接计算条件概率 P(y|x) ，我们将最大的 P(y|x) 作为新样本的分类。判别式模型是对条件概率建模，学习不同类别之间的最优边界。而生成式模型计算样本 x 的联合概率 P(x,y) ，然后根据贝叶斯公式： $ P(y|x)=\frac{P(x,y)}{P(x)} $, 分别计算P(y|x)，选择三类中最大的P(y|x)作为样本的分类。故A，C选项正确，生成式模型可以理解为在尝试还原数据原来的联合分布，判别式模型直接对后验概率建模，B选项显然正确。

5、贝叶斯主义一般做____（点/分布）估计

分布

6、下列说法错误的是（）

1. 贝叶斯学习≠贝叶斯分类器
2. SVM属于统计学习
3. 用到了贝叶斯公式就是贝叶斯学习
4. 贝叶斯分类器是生成式模型

7、下列说法错误的是（）

1. 极大似然估计做了独立同分布假设
2. 极大似然估计的任务是利用训练集估计参数
3. 极大似然估计需先假设某种概率分布形式
4. 极大似然估计属于贝叶斯主义

本题选D。极大似然估计是典型的频率学派观点，它的基本思想是：待估计参数 θ 是客观存在的，只是未知而已，当 θm 满足“ θ=θm 时，该组观测样本 (X1,X2,…,Xn)=(x1,x2,…,xn) 更容易被观测到“，我们就说 θm是 θ 的极大似然估计值。也即，估计值 θ^mle 使得事件发生的可能性最大。现在看其他选项，极大似然估计需要iid假设，A正确；极大似然需要用训练集估计参数，B正确；极大似然分布首先要假设分布形式，才能确定参数，C正确。

8、极大似然估计中，对数似然的解与原问题____（一致/不一致）

一致

9、下列说法错误的是（）

1. 计算 P(x|c) 主要障碍之一是组合爆炸
2. 计算 P(x|c) 主要障碍之一是样本稀疏
3. 朴素贝叶斯分类器中，计算离散属性的 $P(x_i|c)$ 需要考虑概率密度函数
4. 朴素贝叶斯分类器中的概率密度函数，可以使用高斯分布

10、考虑二分类问题，若数据集中有100个样本，其中负类样本有48个。令 c 表示正类，则 P© 的估计值是____（保留2位小数）

0.52

在统计中我们可以用频率近似估计概率，故52/100=0.52，保留两位小数后为0.52。

11、考虑如图数据集，其中 x1与x2为特征，其取值集合分别为x1={−1,0,1}，x2={B,M,S}，y为类别标记，其取值集合为y={0,1}。

使用所给训练数据，学习一个朴素贝叶斯分类器，考虑样本x={0,B}，请计算P(y=0)P(x|y=0)的值____（保留2位有效数字）。

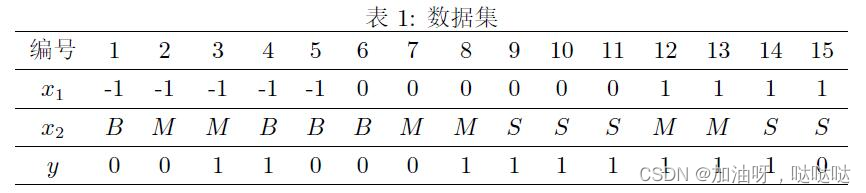
0.067

12、考虑如图数据集，其中x1与x2为特征，其取值集合分别为x1={−1,0,1}，x2={B,M,S}，y为类别标记，其取值集合为y={0,1}。

使用所给训练数据，学习一个朴素贝叶斯分类器，这个分类器会将样本x={0,B}的标记预测为____

0

13、考虑如图数据集，其中x1与x2为特征，其取值集合分别为x1={−1,0,1}，x2={B,M,S}，y为类别标记，其取值集合为y={0,1}。

实际中估计概率值时，常用“拉普拉斯修正”，相关内容请阅读《机器学习》教材第153-154页。

使用所给训练数据，使用“拉普拉斯修正”，学习一个朴素贝叶斯分类器，考虑样本x={0,B}，请计算P(y=1)P(x|y=1)的值____（保留2位有效数字）

0.041

10/17 * 5/12 * 2/12 = 0.041

14、以下哪个选项是生成式模型？

1. 贝叶斯网
2. 对数几率回归
3. 决策树
4. 支持向量机

15、最小化分类错误率的贝叶斯最优分类器为：对每个样本选择能使以下哪个选项最大的类别标记？

1. 后验概率
2. 类条件概率
3. 先验
4. 以上都不是

本题选A。假设样本的真是类别是c类，那么为了最小化分类错误率，我们需要最小化把样本分类到非c类里的概率，也就是要最大化把样本分到c里的概率，即后验概率。