欧拉公式ejwt
In this post we will explore Euler’s Formula, explain what it is, where it comes from, and reveal its magic properties.
在这篇文章中,我们将探索欧拉公式,解释其含义,来源以及揭示其神奇的特性。
什么是欧拉公式? (What is Euler’s Formula?)
Euler’s Formula, coined by Leonhard Euler in the XVIIIth century, is one of the most famous and beautiful formulas in the mathematical world.
由列昂哈德·欧拉 ( Leonhard Euler)在十八世纪创造的欧拉 公式是数学界最著名,最美丽的公式之一。
It is so, because it relates various apparently very distinct elements like the irrational number e, imaginary numbers, and trigonometrical functions.
之所以如此,是因为它涉及到各种明显非常不同的元素,例如无理数e ,虚数和三角函数。
Lets see what it looks like:
让我们看一下它的样子:

As we can see, we have our precious number e on the left, the cosine and sine trigonometrical functions on the right, and our imaginary correspondent i on both sides.
正如我们所看到的,左边有我们的珍贵数字e ,右边有余弦和正弦三角函数,而在两侧都有我们的虚构对应物i 。
Before we dive into what this formula is telling us, both from a calculus and a geometric perspective, lets first see where this crazy relationship comes from.
在深入研究此公式要告诉我们的内容之前,首先要从微积分和几何角度出发,先了解一下这种疯狂的关系的来源。
欧拉公式的历史 (The History of Euler’s Formula)
In the year 1714 British physicist and mathematician Roger Cotes established in one formula the relationship between logarithms, trigonometrical functions and imaginary numbers.
1714年,英国物理学家和数学家罗杰·科特斯(Roger Cotes)用一个公式建立了对数,三角函数和虚数之间的关系。
Twenty years later, Leonhard Euler reached the same formula but using exponential functions instead of logarithms. Cote’s formula is the following:
二十年后, 莱昂哈德·欧拉 ( Leonhard Euler)得出了相同的公式,只是使用了指数函数而不是对数。 科特的公式如下:
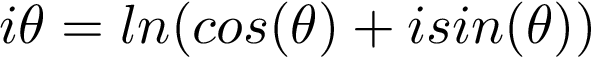
To go from Cotes formula to Euler’s we just have to apply exponentials to both sides. To go from Euler’s Formula to Cotes we reverse this process, using logarithms.
要从Cotes公式转换为Euler公式,我们只需要对双方应用指数。 为了从欧拉公式到科特兹,我们使用对数逆转了这一过程。
Curiously enough, that none of the authors of the respective formulas saw the geometrical connotation, which is one of the most fascinating insights that can be derived from them. The following figure shows the complex plane, the place where we will see these geometrical connotations.
令人感到奇怪的是, 各个公式的作者都没有看到几何含义 ,这是可以从中得出的最引人入胜的见解之一。 下图显示了复杂平面,我们将在其中看到这些几何含义。

Before that, you should know that if we particularise Euler’s formula to the value of θ= π we get the famous Euler’s Identity. Lets quickly see it.
在此之前,您应该知道,如果将欧拉公式特定化为θ =π的值,我们将获得著名的欧拉恒等式 。 让我们快速看到它。
欧拉的身份 (Euler’s Identity)
As mentioned before, if we set the value of θ the probably most famous number of all times, π, Euler’s Formula becomes Euler’s Identity.
如前所述,如果我们将θ的值设置为有史以来最著名的数字π,则欧拉公式成为 欧拉的恒等式 。

If you want to see why Euler’s Identity is so intriguing, check out the following post where I explain all about it.
如果您想了解为什么Euler的身份如此吸引人,请查看以下文章,我将在其中进行所有解释。
Awesome, now that we know what Euler’s Formula and Euler’s Identity are, lets break the former into its individual elements and explore why it is such an amazing equation.
太棒了,现在我们知道什么是欧拉公式和欧拉身份, 让我们将前者分解为单独的元素,并探究为什么它是如此惊人的方程式。
余弦和正弦 (Cosine and Sine)
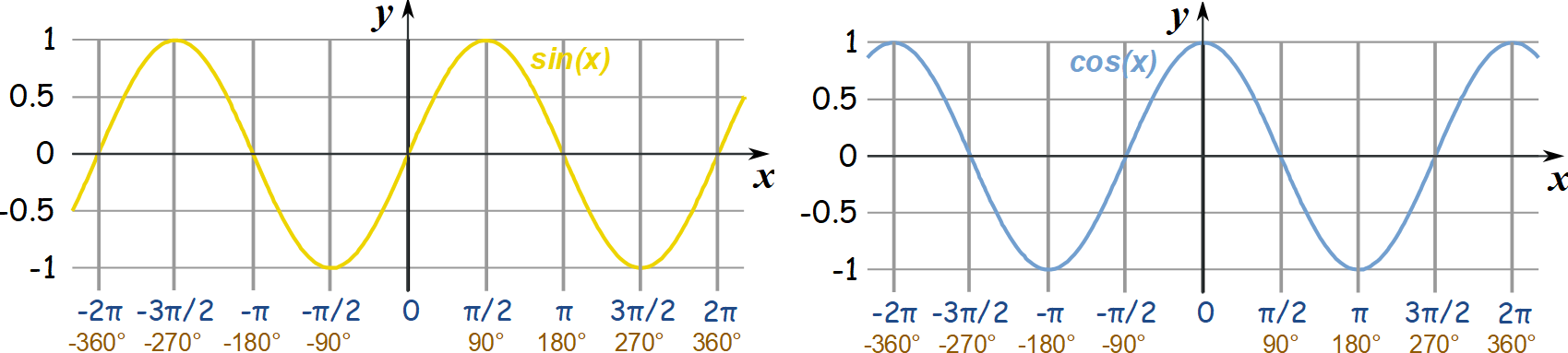
The sine and cosine are periodic trigonometrical functions with a period of 2π. This means that every 2π radians they go back to having the same value. The following figure shows these functions.
正弦和余弦是周期为2π的周期性三角函数。 这意味着每2π弧度它们将返回到相同的值。 下图显示了这些功能。
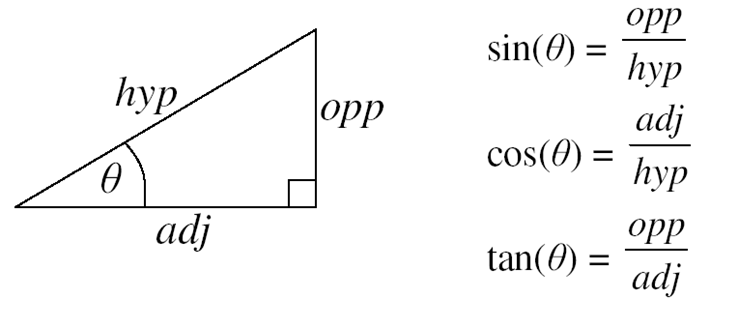
If we look at a triangle with 90º on one of their angles, the sine and the cosine of the angle θ can be calculated using the lengths of the sizes of the sides of such triangle, like shown in the following figure:
如果我们看一个角度为90º的三角形,则可以使用该三角形的边的大小长度来计算角度θ的正弦和余弦,如下图所示:
虚数 (Imaginary numbers)
Initially, numbers were invented to keep track of the count of entire objects. This is how natural numbers were conceived. Then, a mechanism was needed to keep track of when somebody owed someone else an entire object. Integer numbers were born, which were an extension of the previous natural numbers to the negative side.
最初,人们发明了数字来跟踪整个对象的数量。 这就是自然数的构想。 然后,需要一种机制来跟踪某人何时欠别人整个物品。 整数诞生了,它是先前自然数向负数的扩展。
After this, the need to keep track of fractions, or parts of entire objects arose, giving birth to the rational numbers. Finally, numbers that describe fractions whose decimals go on forever (like π) were found in mathematics, and thus irrational numbers were born. All of the previous kind of numbers fall under the category of real numbers.
此后,就需要跟踪分数或整个对象的一部分,从而产生了有理数 。 最后,在数学中发现了描述小数位数永远不变的分数(例如π)的数字,因此诞生了无理数 。 所有先前的数字都属于实数 。
But imaginary numbers are something of a completely different nature.
但是虚数是完全不同的性质。
At their birth, imaginary numbers were conceived as a mathematical tool for being able to operate with squared roots of negative numbers, and the term ‘imaginary’ was kind of derogatory. i, the letter denoting imaginary numbers, is equivalent to the square root of -1.
虚数在诞生之初就被认为是一种能够使用负数平方根进行运算的数学工具 ,而“ 虚数 ”一词是一种贬义。 i是表示虚数的字母,它等于-1的平方根。
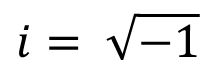
It wasn’t until our beloved Euler showed up, that the square root of -1 was given this letter as a representation, and started being considered useful. After this, it naturally appeared in all kinds of problems from physics like the laws of electricity and magnetism, or wave dynamics.
直到我们心爱的Euler出现 ,才以-1的平方根表示该字母,并开始被认为是有用的。 此后,它自然会出现在物理学中的各种问题中,例如电和磁的定律或波动力学。
无理数e (The irrational number e)
The mathematical constant e is one of the most important numbers in mathematics. This constant, despite getting its name from Euler, and sometimes known as Euler’s number, was discovered before this famous mathematician popularised it.
数学常数e是数学中最重要的数字之一。 尽管这个常数从欧拉得名,有时也被称为欧拉数 ,但在这位著名的数学家推广它之前就发现了它。
Specifically, it was first coined by the prodigious Jacob Bernuilli in 1683 in the study of the compound effect and different calculations regarding the exponential increases of an investment with time. From this point of view, our famous number e was calculated as:
具体来说,它是由伟大的雅各布·伯努利 ( Jacob Bernuilli) 于1683年首先提出的,用于研究复合效应以及关于投资随时间呈指数增长的不同计算方法。 从这个角度来看,我们的著名数e计算为:
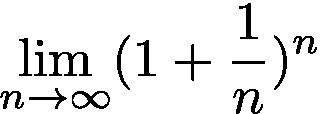
where this limit converges and takes the value we all know for this number of 2,71828.
这个极限收敛并采用我们都知道的2,71828的值。
Despite of this constant being very important, the magic of Euler’s Formula does not come from this precise value, but from the function that this letter’s name has come to steal: the exponential function. Lets check it out.
尽管这个常数非常重要,但欧拉公式的魔力并不是来自这个精确的值,而是来自这个字母名称所窃取的函数 : 指数函数 。 让我们来看看。
指数函数 (The exponential function)
欧拉公式和实数 (Euler’s Formula and Real numbers)
The general concept that we have for an exponential function is that of repeated multiplication:
指数函数的一般概念是重复乘法:

However, what happens when we think about exponentials whose exponent is a square root, a negative number, a fraction, or an imaginary number? The concept of repeated multiplication breaks down. It only holds then the exponent (x in this case) is a positive, integer number.
但是,当我们考虑指数为平方根,负数,分数或虚数的指数时会发生什么? 重复乘法的概念破裂了 。 它只保留指数(在这种情况下为x)为正整数。
Exponential functions are more precisely defined by the following series, one of the famous Taylor Series, which we will call exp(x):
指数函数由以下系列更精确地定义,这是著名的泰勒级数之一 ,我们将其称为exp(x) :
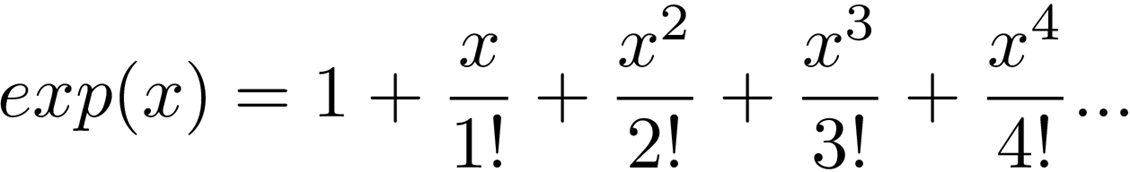
Again, despite seeming infinite this series converges, as the denominator of each fraction grows much faster than the numerator, and the function itself has some amazing properties that allow us to explain the value of fractional and negative exponentials.
同样,尽管看似无限,但该级数收敛,因为每个分数的分母比分子增长快得多,并且函数本身具有一些惊人的属性, 使我们能够解释分数和负指数的值 。
The value of 2,71828 that we know number e for, is the value we get when we input x = 1 into this exponential function, so, for now, we will say exp(1) = e.
我们知道数字e的值2,71828是当我们将x = 1输入此指数函数时所获得的值,因此,现在,我们将说exp(1)= e。
The fundamental and most amazing property of this function is that multiplication in the inputs is equal to the addition of the outputs. Adding the inputs (the number in parenthesis, the x in exp(x)), is the same as multiplying the outputs (the number returned by exp(x)):
此函数的基本和最令人惊奇的特性是输入中的乘法等于输出的相加 。 将输入相加(括号中的数字,exp(x)中的x)与将输出相乘(exp(x)返回的数字)相同:
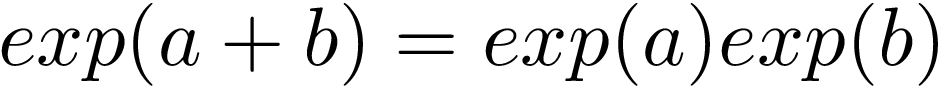
Try it out yourself. Get a calculator and calculate the following:
自己尝试一下。 获取计算器并计算以下内容:
exp(3) = 20.0855
exp(3)= 20.0855
epx(4) = 54.5981
epx(4)= 54.5981
exp(3)exp(4) = 1096.6331
exp(3)exp(4)= 1096.6331
exp(3 + 4) = exp(7) = 1096.6331
exp(3 + 4)= exp(7)= 1096.6331
Cool right? Adding the inputs of the exponential functions (3 and 4) is the same as multiplying the individual outputs (exp(3) and exp(4)).
酷吧? 将指数函数(3和4)的输入相加与将各个输出(exp(3)和exp(4))相乘相同。
This is not at all trivial, and is probably something nobody would have guessed by just looking at the polynomial Taylor Series. However, it is an awesome property which allows us to answer some of the previous questions.
这一点都不微不足道 ,可能只是看多项式泰勒级数就不会有人猜到。 但是,这是一个了不起的属性,它使我们能够回答前面的一些问题。
Exponentiating a number to 1/2 means calculating the squared root of that number. How can this be? Lets work it out with the previous property of the exponential function.
将数字取幂等于1/2意味着计算该数字的平方根。 怎么会这样? 让我们使用指数函数的先前属性进行计算。
exp(1/2 + 1/2) is equal to exp(1) which is e. exp(1/2 + 1/2) is also equal to exp(1/2)exp(1/2). So exp(1/2) squared is equal to e and therefore exp(1/2) is equal to the squared root of e. Fantastic.
exp(1/2 + 1/2)等于exp(1) ,即e。 exp(1/2 + 1/2)也等于exp(1/2)exp(1/2) 。 因此exp(1/2)的平方等于e ,因此exp(1/2)等于e的平方根。 太棒了
2. Exponentiating a number to 0 is equal to 1. We know this thanks to the polynomial Taylor Series when x = 0.
2. 对数字求幂等于1 。 我们知道这要归功于x = 0时的多项式泰勒级数。
3. Exponentiating a number to -1 is equal to dividing 1 by that number. This can be easily derived from knowing that exp(0) = 1.
3.对一个数字求幂等于-1等于将该数字除以1。 这可以从知道exp(0)= 1轻松得出。
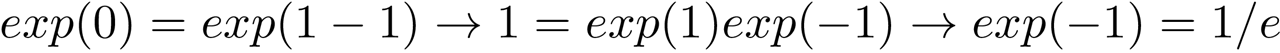
Now, what happens when we take the exp function and insert an imaginary number in it?
现在,当我们使用exp函数并在其中插入一个虚数时会发生什么?
欧拉公式和复数 (Euler’s Formula and Complex numbers)
To see the results of doing this, we need to go back to the complex plane. Lets evaluate complex numbers that exist on the unit circle, painted in pink.
要查看执行此操作的结果,我们需要回到复杂平面。 让我们评估粉红色涂在单位圆上的复数。
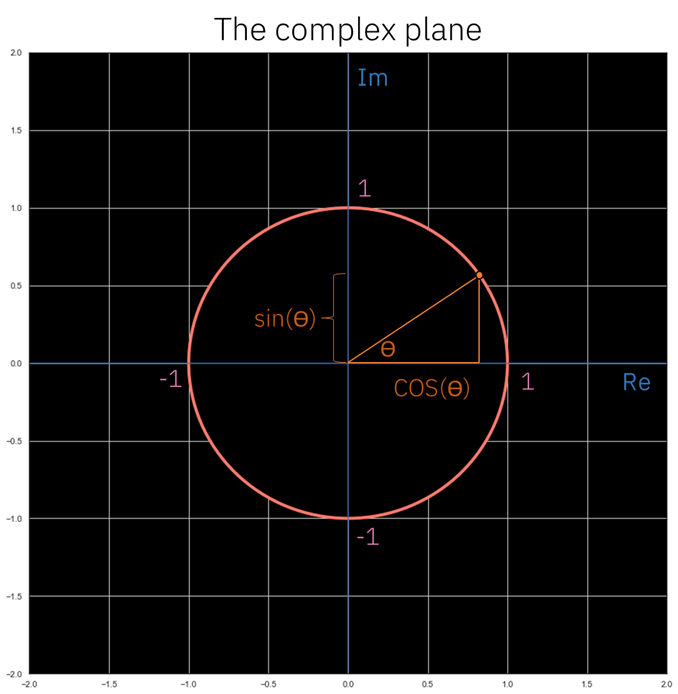
Imagine we have the previous imaginary number, described by Euler’s formula and represented in the complex plane by the orange dot.
想象一下,我们有一个先前的虚数,它由欧拉公式描述,并在复平面中由橙色点表示。
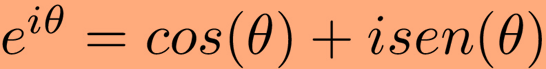
What happens in our exponential function, if we give it an imaginary number as an argument? What is exp(i θ)?
如果我们给它一个虚数作为参数,指数函数会发生什么? 什么是 exp( iθ) ?
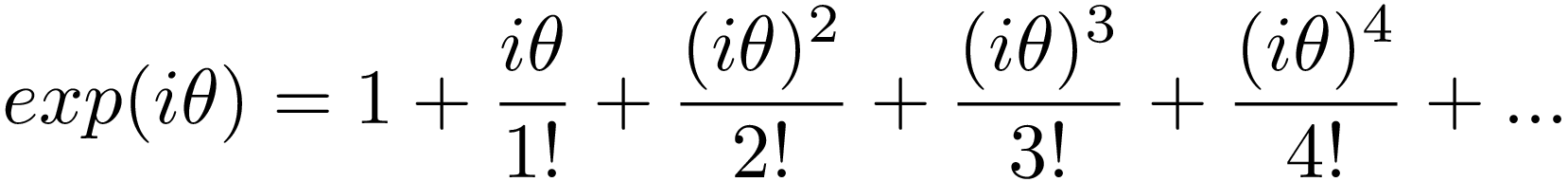
Lets pick an specific value for θ and see what comes out of there. If we take θ = 1, and calculate the first 20 elements of exp(i) we get the complex number 0.5403 + 0.8414i. This is the same value that we get from Euler’s Formula, using the cosine and the sine.
让我们为θ选择一个特定的值,然后看看其中的结果。 如果我们使θ= 1,并计算exp(i)的前20个元素,我们将得到复数0.5403 + 0.8414i 。 这与我们使用余弦和正弦从欧拉公式中获得的值相同。
It is quite interesting, however, to see how by adding more and more elements in the Taylor series, this calculation becomes more precise, and how this is done geometrically. The following list shows how the value of exp(i) becomes more and more accurate as we take into account more and more elements of the previous series.
然而,很有趣的是,看看如何通过在泰勒级数中添加越来越多的元素 ,使该计算变得更加精确 ,以及如何在几何上完成该计算 。 以下列表显示了随着我们考虑先前系列中越来越多的元素, exp(i)的值如何变得越来越准确。
exp(i) with 1 element in the Taylor series: 1
泰勒级数中具有1个元素的exp(i) :1
exp(i) with 2 elements in the Taylor series: 1 + i
泰勒级数中有2个元素的exp(i) :1 + i
exp(i) with 3 elements in the Taylor series: 0.5 + i
泰勒级数中包含3个元素的exp(i) :0.5 + i
exp(i) with 4 elements in the Taylor series: 0.5 + 0.83333i
泰勒级数中包含4个元素的exp(i) :0.5 + 0.83333i
exp(i) with 5 elements in the Taylor series: 0.541666 + 0.83333i
泰勒级数中有5个元素的exp(i) :0.541666 + 0.83333i
exp(i) with 6 elements in the Taylor series: 0.541666 + 0.841666i
泰勒级数中包含6个元素的exp(i) :0.541666 + 0.841666i
exp(i) with 7 elements in the Taylor series: 0.5402777 + 0.841666i
泰勒级数中有7个元素的exp(i) :0.5402777 + 0.841666i
exp(i) with 8 elements in the Taylor series: 0.5402777 + 0.841468i
泰勒级数中包含8个元素的exp(i) :0.5402777 + 0.841468i
exp(i) with 9 elements in the Taylor series: 0.5403025 + 0.841468i
泰勒级数中有9个元素的exp(i) :0.5403025 + 0.841468i
Cool right? Now, lets see something even cooler. The following figure shows the plots of the values of exp(i) as we increase the number of elements considered in the Taylor Series. Each yellow line ends at the value of the complex number calculated with that many elements, and represents an extra addition to the previous one.
酷吧? 现在,让我们看一些更酷的东西。 下图显示了随着我们增加泰勒级数中考虑的元素数而得出的exp(i)值的图 。 每条黄线的结尾都是用这么多元素计算出的复数的值,并表示对前一个元素的额外加法。
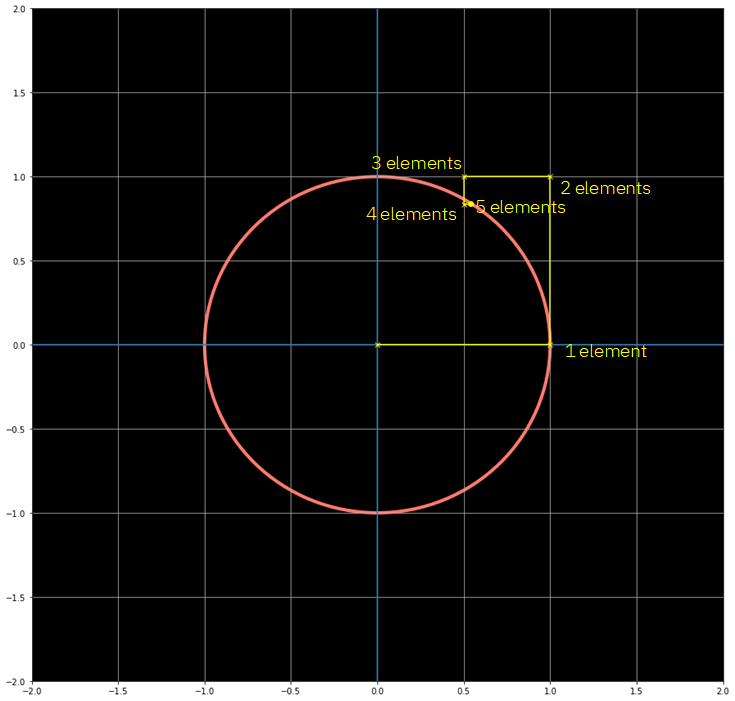
As we can see, a kind of spiral is formed, that gets closer and closer to the final value of the exponential that we can verify with Euler’s Formula. This is awesome, and it tells us something really beautiful about exponentials.
如我们所见, 形成了一种螺旋 , 这种螺旋越来越接近我们可以用欧拉公式验证的指数的最终值 。 这太棒了,它告诉我们有关指数的某些知识。
Independently of the value of θ, if we use enough elements of the polynomial series exp(iθ) always ends up in the unit circle, with a rotation around it of θ radians.
独立地θ的值的,如果我们使用多项式系列EXP(Iθ)的足够的元素总是在单位圆结束,与它周围的旋转θ弧度。
This is shown in the following figures, where the same plot as before has been created for different values of θ.
如下图所示,其中针对不同的θ值创建了与以前相同的图。
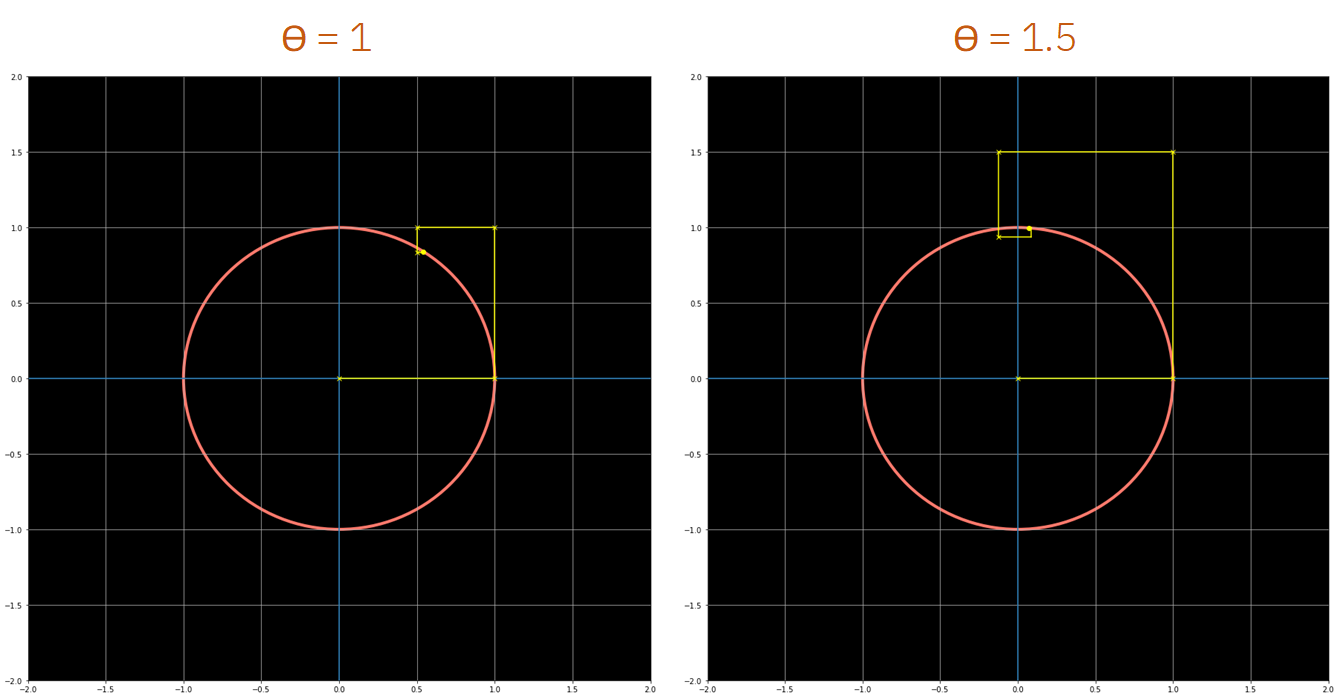
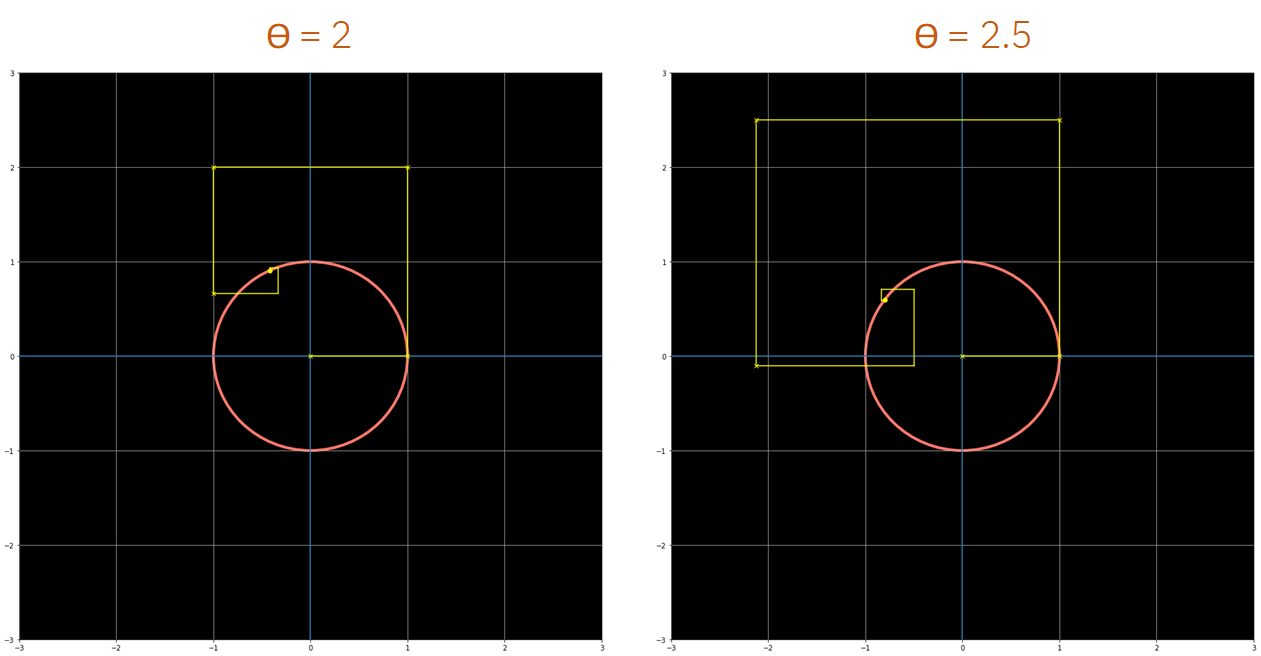
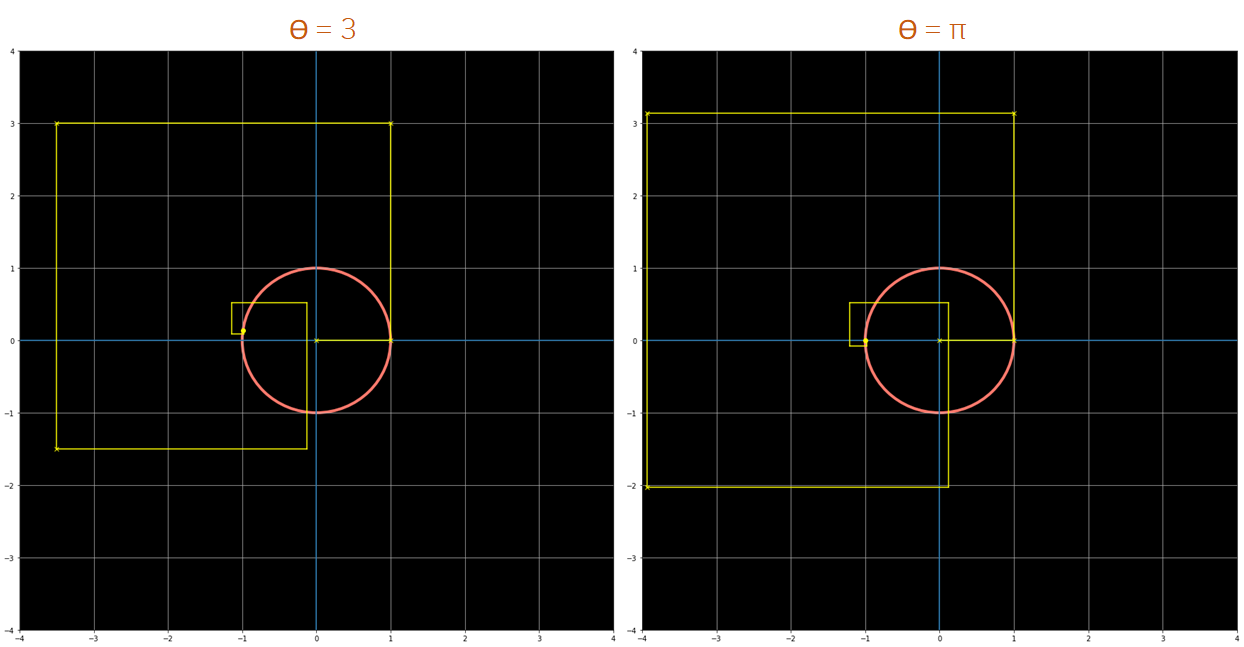
As we can see from the previous figures, exp(iθ) always ends up in the unit circle if enough elements from the series are used. For any value of theta that we use, if we take enough elements of the polynomial series this always happens, just by adding, rotating and multiplying these yellow lines that represent an additional element of the series.
从前面的图中可以看出,如果使用了序列中足够的元素, exp(iθ)总是以单位圆结束。 对于我们使用的任何theta值,如果我们采用多项式级数的足够多的元素,则总是会发生这种情况 ,只需将代表该系列的另一个元素的黄线相加,旋转和相乘即可。
Also, you might have noticed already, but in the last figure (θ = π) what we are plotting is Euler’s Identity. Lets recover the formula, because this last plot also contains some beautiful insights:
另外,您可能已经注意到,但是 在最后一个图中(θ=π),我们绘制的是欧拉身份 。 让我们恢复公式,因为这最后一个图也包含一些美丽的见解:

If we plug in (θ = π), we get Euler’s Identity, which mathematically and geometrically tell us this: by raising a constant(e) to iπ, we walk a distance of π around the unit circle, and we arrive at the point -1, with no imaginary part, which is also the right side of the formula.
如果插入(θ=π) ,我们得到欧拉恒等式,该恒等式在数学和几何上告诉我们:通过将常数( e ) 增大到iπ ,我们在单位圆周围走了π距离,然后我们到达了点-1,没有虚部,也是公式的右侧。
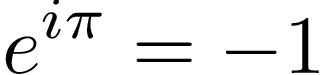
Geometrically, as we’ve seen, this all happens by rotating vectors and multiplying their lengths.
如我们所见,在几何上, 所有这些都是通过旋转向量并乘以它们的长度来实现的。
This is completely baffling!
这简直令人莫名其妙!
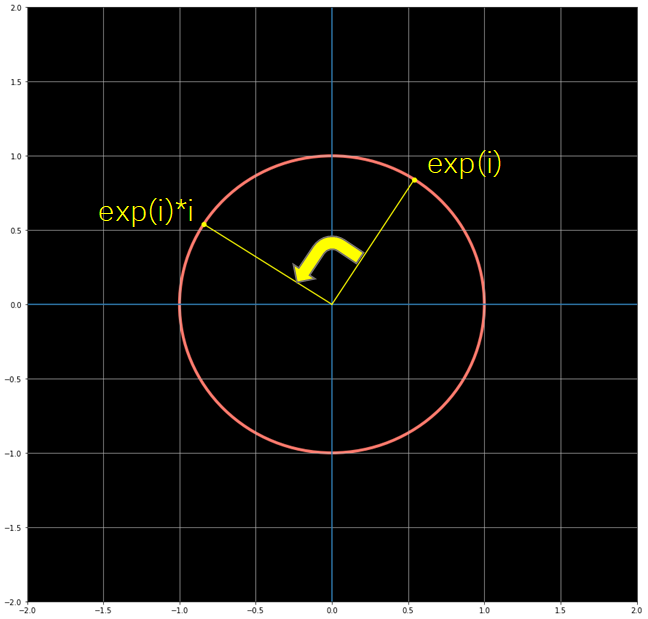
One of the main reasons that this comes to be, is what happens in the complex plane when we multiply a number by i. Multiplying by i implies a 90º rotation from the origin around the unit circle, like shown in the following figure.
造成这种情况的主要原因之一是,当我们将数字乘以i时,复平面中会发生什么。 乘以i意味着从原点绕单位圆旋转90º ,如下图所示。
结论 (Conclusion)
Euler’s formula is one of the most beautiful formulas of our days. It beautifully connects many different elements, and its geometrical interpretation and origin are something completely wonderful.
欧拉公式是当今最美丽的公式之一。 它精美地连接了许多不同的元素,并且它的几何解释和起源完全是一件美妙的事。
It is like nature is trying to tell us something with it.
就像大自然试图用它告诉我们一些事情。
I hope this post has made you learn and taught you the fascinating insights behind Euler’s Formula.
我希望这篇文章能使您学习并教给您Euler公式背后的迷人见解。
Feel free to follow me on Twitter at @jaimezorno. Also, you can take a look at my posts on Data Science, Maths and Machine Learning here. Have a good read!
请随时通过@jaimezorno 在Twitter上关注我 。 另外,您也可以看一下我在数据科学,数学和机器学习方面的文章 在这里 。 祝您阅读愉快!
For more posts like this one follow me on Medium, and stay tuned!
对于更多这样的帖子 在Medium上关注我 ,敬请期待!
If you wish to learn more, the following Channel has some awesome videos on Euler’s Formula, Euler’s Equation and the intuition behind complex numbers.
如果您想了解更多信息,请在下面的频道中观看有关Euler公式,Euler方程以及复数背后的直觉的精彩视频。
欧拉公式ejwt




 本文深入探讨了欧拉公式ejwt,揭示了其数学之美。欧拉公式是复数领域的一个基本关系,将三角函数与指数函数联系起来,具有广泛的应用于物理学、工程学和计算机科学中。
本文深入探讨了欧拉公式ejwt,揭示了其数学之美。欧拉公式是复数领域的一个基本关系,将三角函数与指数函数联系起来,具有广泛的应用于物理学、工程学和计算机科学中。
















 3504
3504

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








