与 e^jωt 相关的公式 | 图像及性质

注：本文为 “$e^{j\omega t}$” 相关文章合辑。

未全整理。

---

傅里叶变换的相关公式

月疯于 2018 - 06 - 04 17:02:21 发布

欧拉公式相关：

在复分析领域，有如下欧拉公式相关等式：

• $e^{-j\omega t}=\cos (\omega t)-j\sin (\omega t)$

• $e^{j\omega t}=\cos (\omega t)+j\sin (\omega t)$

由上述两式可推导出：

• $\sin (\omega t)=\frac{1}{2j}(e^{j\omega t}-e^{-j\omega t})$

• $\cos (\omega t)=\frac{1}{2}(e^{j\omega t}+e^{-j\omega t})$

关于以上公式，参见复分析领域欧拉公式相关内容。

傅里叶变换相关：

• 基于上述公式，傅里叶级数、傅里叶变换/反变换等相关公式可改写成 “$e$ 的指数形式”。

• $e^{j\omega t}$ 在复平面中可作为一个 “基”，因为它包含了实轴（实数单位 “$1$”）和虚轴（虚数单位 “$j$”）上两个正交的 “基”，这解释了为何能用傅里叶方法 “分解” 很多函数。

---

关于 $j\omega$ 和 $e^{j\omega t}$ 的领悟

xkf321 于 2017 - 05 - 05 10:27:54 发布

疑惑：

在看到《电磁场与电磁波》时变电磁场一章中出现 $j\omega$ 和 $e^{j\omega t}$ 后，对诸如电感的阻抗为何可表示成 $j\omega L$ 存疑，不明白 $j\omega$ 的推导及为何能与 $L$ 相乘。

解析：

对于正弦信号 $\alpha ={\alpha }_0+\omega t$，关于角度求导等同于关于时间 $t$ 求导，即 $d\alpha =\omega dt$，所以在正弦信号前提下，$j\omega$ 与关于时间求导等价，且 $j\omega$ 是 $e^{j\omega t}$ 对时间求导得到的。

以电感为例，其两端电压电流关系为 $u=L\frac{di}{dt}$，将 $u$ 和 $i$ 写成复数形式 $u\cdot e^{j\omega t}$，$i\cdot e^{j\omega t}$，则原式变为：

$$\begin{array}{rl}u\cdot e^{j\omega t}& =L\cdot \frac{d(i\cdot e^{j\omega t})}{dt}\\ & =L\cdot i\cdot j\omega \cdot e^{j\omega t}\end{array}$$

两端同时消去 $e^{j\omega t}$，可得

$u=L\cdot i\cdot j\omega$

根据欧姆定律 $Z=\frac{u}{i}$，则

$Z=j\omega L$

---

复指数信号 $e^{j\omega t}$ 的图像及性质

山泼黛 发布 2021 - 10 - 26 16:53:16

在信号与系统、数字信号处理、信号分析等领域，傅里叶变换是核心工具，而复指数信号 $e^{j\omega t}$ 是傅里叶变换的基础。

对于 $e^{j\omega t}$，尽管看似熟悉，但当被问及它的本质、特性以及相关性质时，可能很多人无法立刻作答。

首先，在复指数信号 $e^{j\omega t}$ 中，$j$ 为虚数单位，$\omega$ 是角频率（通常为常量），$t$ 是时间变量。

关于虚数单位 $j$，需回顾复数的基本概念。复数一般表示为 $a+bj$，其中 $a$ 和 $b$ 为实数。

在复平面上，复数可用一条线段表示，线段长度对应复数的模$|a+bj|=\sqrt{a^2+b^2}$，线段与实轴（横轴）的夹角对应复数的相位 $\theta =\arctan \left(\frac{b}{a}\right)$。

由于 $e^{j\omega t}$ 包含时间变量 $t$，因此它是一个复指数信号。理论上，可通过分析其在复平面上的变化来绘制其图像。

以下为使用 Matlab 绘制 $e^{j\omega t}$ 图像的代码示例：

w = 1;
t = 0:0.1:20;
f = exp(1j*w*t); % 语法问题，写代码最好用 1j 代替 j
x = t;
y = imag(f);
z = real(f);
figure;
plot3(x, y, z, '.b');
xlabel('时间 t');
ylabel('虚部 y');
zlabel('实部 z');

通过上述代码，得到了 $e^{j\omega t}$ 的图像，如下所示：

需注意，上图中 $x$ 坐标的方向与常规稿纸绘图时的方向存在差异。在诸多相关图形中，普遍未对自变量所在的轴作出明确标注，这是引发理解困惑的因素之一。

从绘图原理而言，通常是先为自变量赋予一系列取值，进而在坐标系中进行描点操作，最终将这些点连接成线。

在本图中，每一个点对应于 $t$ 取值为 $t_0$ 时 $e^{j\omega t_0}$ 的值。依据欧拉公式：

$e^{j\omega t_0}=\cos (\omega t_0)+j\sin (\omega t_0)$

由此得出的函数值为复数形式。由于复数的完整表示需要两个坐标轴，这便解释了为何绘制出的图形呈现为三维形态。

接下来，对该图形展开解析，以探究其内在性质。

首先，将图中所有的点向 $yOz$ 平面进行投影，所得结果将是一个圆形。原因在于：

$e^{j\omega t}=\cos (\omega t)+j\sin (\omega t)$

根据三角函数的基本关系 ${\cos }^2(\omega t)+{\sin }^2(\omega t)=1$，即其实部与虚部的平方和恒为 $1$。所以，$e^{j\omega t}$ 在复平面上的几何表示即为一个单位圆，如下图所示：

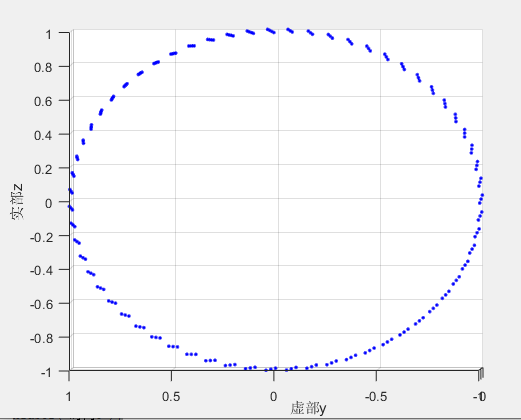
Matlab 画出来的三维图可拖曳从不同角度观察，此图是拖到一个从 $x$ 轴看过去的角度。

其次，关于 $\omega$ 的物理意义和性质，从上面那幅图可看到一个不断螺旋前进的轨迹图，$\omega$ 反映了旋转的快慢。

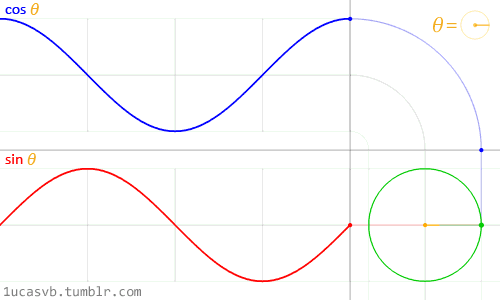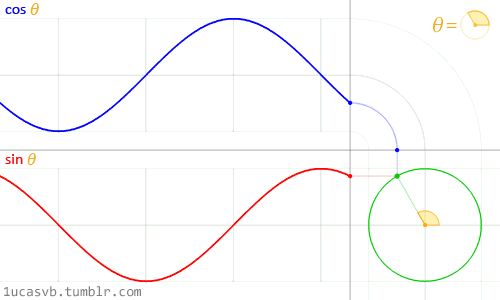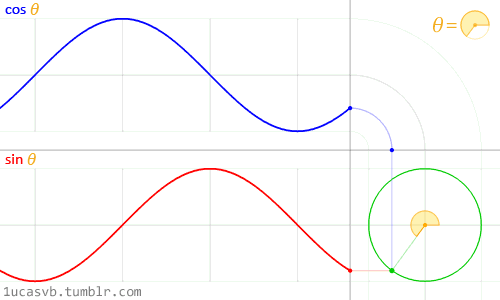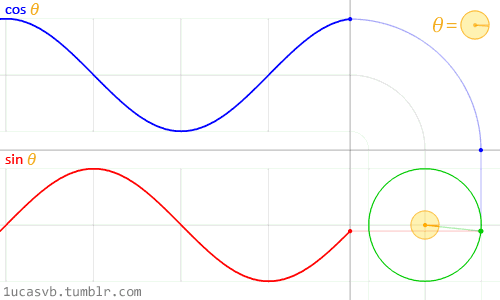
最后，$e^{j\omega t}$ 还可看做一个单位长度、逆时针旋转的复平面旋转向量，如下图所示：

---

关于傅利叶变换的一些数学解解释兼及其它

原文地址：关于傅利叶变换的一些数学解释 （链接已沉寂）

作者：上星

[转自饮水思源 EE]

向前进，你就会产生信念。
—— 达· 朗贝尔

傅利叶变换是信号系统的奠基石，小波分析的基础理论，理论的粗疏理解固然不难但是要达到深刻的境界，是不能仅仅依靠教科书的。

由于本次讨论持续时间较长，参与面较广，合集再给予 $m$ 之后效果反而不佳。

为避免讨论湮没，因此在此简略加以总结，鄙下仅仅负责发帖，所有版权全部归于以下几位 IE 学长：

Valetine，QueueingSys，zekong，vole，filestorm，dwang

Q1: 为何要在通讯中使用傅利叶变换？(fingers)

A11:

一个函数的傅立叶变换，本质上是把函数分解到一个垂直的坐标系，每个坐标分量称为频率，在这个坐标系下的系数（本身是一个函数），我们称它为这个函数的频谱。

人们想理解怎么样能够控制信号在不同频率下传递，因为自然介质对不同频率信号响应不同。然后还要考虑如何能够在改变信号频率前后，最小程度的减小或者增大某些量，比如信噪比，或者熵，或者其他度量。傅立叶变换可以对这些问题提供工具。数学上，也更容易操作。

傅立叶变化在工程和物理中使用十分广泛。（Valetine）

A12:

Fourier Transform是把给定信号用一大堆简单周期信号做一个线性叠加。

那一大堆简单的周期信号可以认为是基。这个基很 $nb$，具有很多性质，比如正交。同时，还存在一种快速算法。所以总的来说 Fourier Transform 实在是只应天上有的完美理论。(filestorm)

Q2: 如果对于本身是正旋波的信号，频率比如说是 $5MHz$，做过傅立叶变换，那频率是否仍然还和原来相同？

A21:

正弦波做傅立叶变化后就不是周期性的了，所以也就不存在什么频率了，但是这个变化的冲激是位于 $5MHz$ 和 $-5MHz$ 处 (dwang)

A22：

首先，Fourier 变换只是给人们提供另一个视角去看信号而已。

有人认为时域看信号直观些

有人认为频域看信号直观些

还有人喜欢即从时域又从频域看信号，这要看应用场合的。

讲得再远点，除了时域和频域，你还可以从 $s$ 域去看信号呢 (利用Laplace变换)

另外，同一个信号，是周期就是周期的，不是周期就不是周期的，无论你从哪个域去看。

从时域看一个 $sinewave$，以时间为 $x$ 轴，信号的波形是 $repeated$ 的，

所以人们很直观地认为那是 “周期的”

从频域看一个 $sinewave$，以频率为 $x$ 轴，信号的 “频谱” 是2根 “脉冲”

但它仍有频率，仍是周期的。(QueueingSys)

A23:

傅立叶变换是一个数学工具，它能把信号对角化到不同的频率。但是信号本身的性质和傅立叶变换没有关系，就是说，不管你做不做傅立叶变换，一个信号还是它本身，比如 $5Mhz$ 依然不变。只是换了坐标系来考虑和处理信号，在这个坐标系下操作的好处，就是所有的频率对应于某一个内积是垂直的。(Valetine)

A24:

$X_1+X_2+X_3+..+X_n$ 三个未知数服从不同的分布，想求在其和小于常数 $K$ 的概率。

一种是在时域上解的话是 $n$ 重积分，极其繁琐。

一种是用蒙托卡罗模拟，但得到的结果不是解析解，有方差。

一种是用傅立叶变换变到频域，指数项使 $+$ 变成了 $\times$，化简以后，使用反变换，这里有很多快速数值算法，比如经典的Euler算法。这要比第一种简单很多。

假设你对 $T$ 时间内的 $invariant$ 的分布建了模，而你在其分布特性不变的假设下想求 $NT$ 时间的分布的话，如果 $T$ 时间分布模型是使用拟和等统计方法得到的话，时域是根本无法得到的。只有转到频域利用 $projection$ 的特性，再转回来。(zekong)

A25:

信号无论在哪个空间下，都是有频率的。但是上文说到的 “不存在频率” 是指 Fourier Spectrum上再对 $frequency$ 求 $frequency$，一般来说，这很难找到一个说得通的物理解释。

但这个操作是有据可查的，叫做 $Liftering$，一般工程上 Fourier Analysis 文献甚少有纪录而已。实际上是可以用来做一些奇怪的检测。(filestorm)

Q3: 谈谈傅立叶变换

A31:

感觉大多咱们研究的都是实直线上的可测函数类，这里可测指的是Lebesgue可测（勒贝格可测），如果说 $L^p(\mathbb{R})$ 指的是 $\mathbb{R}$（实直线）上的可测类，则应该满足：

${\int }_{\mathbb{R}}|f(x){|}^{p}dx$ 有界

$L^{\infty }(\mathbb{R})$ 指的处处有界函数类

一般来说感觉咱们研究的傅立叶变化实际只是很初等的 $L^1(\mathbb{R})$ 上的，$L^2(\mathbb{R})$ 本身 $L^p$ 空间就是一个Banach空间，成立Minkowski不等式，Holder不等式，及 Schwarz 不等式，赋予内积后，即变成一个Hilbert空间。

当 $f(x)\in L^1(\mathbb{R})$ 时，$F(\omega )\in L^{\infty }(\mathbb{R})$，并且再 $L^1(\mathbb{R})$ 上一致连续

如果 $f(x)\in L^2(\mathbb{R})$，那么傅立叶变换是 $L^2$ 空间到 $L^2$ 空间的映射

如此有很多值得分析的结论和定理…

分析学东西很多，虽然都很精彩但理解起来总突然感觉自己原来还是很多不清楚。对于咱们工程应用更是接触的少，比如随机过程就算搞的再熟，也不过就是多了几种建模方法而已，什么排队论啥的而已。当一旦发现如果 $A$ 是 $X$ 的一个 $\sigma$ 环，$(A,X)$ 构成一个可测空间，$\mu X=1$ 时可测集变成了随机事件，而 $(A,X)$ 才构成了概率可测空间时，才发现我们学很多东西是忽略的东西更多。(vole)

A32:

如果要从泛函的角度讨论的话，那么数学分析里一些最困难的问题都会归结到傅立叶分析（或者调和分析）上。

工程上，大部分时候都是以 “拿来主义” 的态度，数学家列个表格傅立叶变换，工程师直接用就是了。但是如果真的要从定义出发，很多非常常用的函数，就很难做傅立叶变换。

比如冲击信号，阶跃信号，或者高斯分布，要严格的定义的话，需要用泛函的知识。前面的讨论就是这些知识的基础。

当然如果不研究数学，并不影响任何人用这些结论。

理解傅立叶变换基本的性质，稍微看一些调和分析，泛函的书（如果你觉得有必要知道那些列表是怎么来的），多想想为什么要用卷积来描述系统对信号的响应（对卷积的理解很可能是最重要的），这些基本问题个人认为是核心。

而且可以看到，同样是傅立叶分析，大家的讨论却是大相径庭，有从 $estimation$ 的角度，有从纯数学的角度，等等。这也能说明这个理论的重要，和它广泛的应用。(valetine)

A33：

说到 $Entropy$，刚好正在写一点东西。忍不住再说两句。尽量用大白话说。

同一个信号，可以通过各种基底 $B$ 和系数 $c$ 的表达。比如我们可以算 $H(c)$，那么这个熵实际上就表达了待表达信号与基底的相似性。或者也可以说，是用那个基底来表达这个待表达信号的复杂程度。

如果直接对原信号 $x$ 求 $H(x)$，那实际上默认了基底是 $I$，如果用 FourierBasis 来求，那么默认了基底是 $e^{i\omega t}$。

但是如果用 Fourier 基底表达大白纸上一个小黑块儿，显然就没有用空域直接表达来得方便。同理，如果在时域表达一个和弦信号，就不如 Fourier 更好地表述了其内蕴的物理模型。

总结一下：从 $Entropy$ 的角度，我们可以看出在某种表达的复杂程度，尽量选择那些有物理背景的表达，会使得分析的难度大大简化。

具体地说，通讯里面信息很多是承载在周期变化的物理模型上的，对于波的分析，自然 Fourier 会有一定优越性了。（filestorm）

Q4: 谈谈卷积（valetine）

• 1，卷积本身是一个理论的，$convolutioncalculus$。

刚开始学信号系统的话，一般总会对这个操作感到奇怪，

比如信号 $f(x)$，$LTI$ 系统冲击响应 $g(x)$

比如信号 $f(x)$，$LTI$ 系统冲击响应 $g(x)$

为什么一个 $LTI$ 系统对信号的响应是 $f(x)$ 和 $g(x)$ 的卷积？而且什么是卷积呢？

要比较让人满意的理解这个问题，一般是需要一点数学知识的。

稍微离点题，一般的说，函数可以理解为把一些点映射到另一些点上的操作， 如果我们现在要建立一个操作，可以把一些函数映射到另一些函数上，我们说这个操作是 $operator$。一个简单的对函数的操作，可以是微分 $\frac{df(x)}{dx}$，积分 $\int f(x)$，等等。

那么系统就是一个 $operatorL$，输入一个信号 $f(x)$，输出一个信号 $u(x)$。表示成 $L(f(x))=u(x)$。

现在想象一个 $LTI$ 离散系统，我们放入一个冲击 $\delta (x)$，系统输出信号 $g(x)$，如果我们把输入信号分解成很多 $c(t)\delta (x-t)$ 的和，$c(t)$ 表示信号在某个时间的大小（如果是复数的话，还有相位），$t$ 表示延迟的多少，那么因为是线性系统，我们可以把输出叠加，而且是非时变系统，所以每个 $\delta (x)$ 的响应仅仅是时间上的延迟。所以输出的结果就是

$\sum c(t)g(x-t)$

这就是所谓的离散和形式。同样的道理，如果系统是连续的，那么这个和的形式就变成积分。我们称之为卷积。

• 2，现在我们试图来解释，为什么傅立叶变换后，时域上的卷积，变成频域上的乘积？

当然我们可以从定义出发，做 $f(x)\ast g(x)$ 的傅立叶变换，然后换变量，就可以分成 $F(j\omega )$ 和 $G(j\omega )$ 的乘积。但是这个基本上是做数学游戏，不是让人觉得满意。

现在我们换个角度来考虑。

首先要我们需要 $LTI$ 系统的一个性质，频率响应。

简单的说，一个 $LTI$ 系统对于正弦信号的输出，也是一个正弦信号，而且信号的周期不变，变换的是信号的幅度和相位。这个特点本质上是因为 $e^{j\omega x}$ 是微分算子的特征方程，就是说对 $e^{j\omega x}$ 求导以后，还是它本身，变化的仅仅是幅度和相位。

$\frac{d}{dx}{e}^{j\omega x}=j\omega e^{j\omega x}$

从这里自然就会展开去很多概念，比如传输方程，特征根等等。

然后我们来考虑 函数 $f(x)=e^{jnx},n$ 是自然数

这个函数周期为 $\frac{2\pi }{n}$。而且有一个非常重要的性质就是，$e^{jnx}$，$e^{-jmx}$。在 $[0,2\pi )$ 上的积分满足

${\int }_0^{2\pi }{e}^{jnx}{e}^{-jmx}dx=0$，如果 $n\ne m$；

${\int }_0^{2\pi }{e}^{jnx}{e}^{-jmx}dx=2\pi$，如果 $n=m$。

我们称这个性质为函数垂直。我们可以把自然数扩展到所有实数，积分从 $[0,2\pi )$ 扩展到 $(-\infty ,+\infty )$，那么 $e^{j\omega x}(w\in \mathbb{R})$ 构成一个垂直的坐标系。

最后我们考虑傅立叶变换。

$F(j\omega )={\int }_{-\infty }^{+\infty }f(x)e^{j\omega x}dx$

有了垂直坐标系的概念后，我们可以把傅立叶变换理解为一个函数在不同特征方程的分量。 比如说，$f(x)=\cos (x)$，一个周期 $2\pi$ 的信号，那么 $F(j\omega )$ 就是两个在 $-1$ 和 $+1$ 的冲击。之所以我们把信号放在频域里，就是因为不同频率的信号，它们相对与一个内积（这里的内积就是以上的积分）是垂直的。

有了以上的概念以后，就可以理解卷积定理了。

• 3，有了特征方程垂直的概念后，我们来看卷积定理。

首先我们做傅立叶变换，把信号 $f(x)$ 分解到不同的特征方程 $e^{j\omega x}$ 上。

对于确定的 $w$，$F(j\omega )$ 就是这个数，表示 $f(x)$ 在 $e^{j\omega x}$ 上的分量。

然后我们让 $w$ 变化，于是 $F(j\omega )$ 是一个函数，我们称它为 $f(x)$ 的频谱。

前面提到 $LTI$ 系统的频响，输入 $e^{j\omega x}$，输出 $g(j\omega )e^{j\omega x}$，变化的是幅度和相位，这些信息都包含在系数 $g(j\omega )$ 中。

现在我们让 $w$ 变化，可以测出系统的频响 $G(j\omega )$，到此为止，我们已经把 $f(x)$ 分解，又得到系统频响，那么运用叠加的性质，线性系统的输出很自然就是

$G(j\omega )F(j\omega )$

【最后鸣谢所有八系学长无私奉献自己的心得，这种心得是比什么书上的证明都更珍贵的。】

---

理解 $e^{-j\omega t}$

1. 复平面上的旋转：
   $e^{j\omega t}$ 是复平面上以角速度 $\omega$ 逆时针旋转的单位向量，而 $e^{-j\omega t}$ 是复平面上以角速度 $\omega$ 顺时针旋转的单位向量，代表着负频率的旋转，是逆时针旋转的镜像。

2. 共轭复数：
   若定义 $z=e^{j\omega t}=\cos (\omega t)+j\sin (\omega t)$，则 $e^{-j\omega t}$ 是 $z$ 的共轭复数，即 $\text{conjugate}(e^{j\omega t})=\cos (\omega t)-j\sin (\omega t)=e^{-j\omega t}$，可描述为 $e^{j\omega t}$ 的复共轭。

3. 时域信号的分解：
   在信号处理中，任何实值时域信号可分解为正、负频率分量，$e^{j\omega t}$ 代表正频率分量，$e^{-j\omega t}$ 代表负频率分量，二者是分解时域信号的基函数。

4. 线性时不变系统（LTI 系统）：
   $e^{-j\omega t}$ 是 LTI 系统的重要特征信号，当输入为 $e^{-j\omega t}$ 时，输出是其倍数（幅度和相位可能变化），在分析 LTI 系统频率响应时很有用。

关于 ${\int }_{-\infty }^{\infty }|e^{j\omega t}|dt=\infty$

1. 计算过程：

   • 已知 $e^{j\omega t}=\cos (\omega t)+j\sin (\omega t)$，对其取模可得 $|e^{j\omega t}|=\sqrt{(\cos (\omega t){)}^2+(\sin (\omega t){)}^2}=1$（因为 ${\cos }^2(\omega t)+{\sin }^2(\omega t)=1$）。

   • 所以 ${\int }_{-\infty }^{\infty }|e^{j\omega t}|dt={\int }_{-\infty }^{\infty }1dt$，此积分在整个实数轴上对常数 1 积分，由于积分区间无限，被积函数为常数 1，该积分发散，即 ${\int }_{-\infty }^{\infty }|e^{j\omega t}|dt=\infty$。

2. 实际应用意义：

   • 傅里叶变换的存在性：这表明 $e^{j\omega t}$ 不是绝对可积的，其傅里叶变换在经典意义上不存在，需用广义函数方法定义。

   • 信号分析中的应用：复指数 $e^{j\omega t}$ 是重要基函数，虽本身不是绝对可积，但通过线性组合可构造绝对可积信号，为信号频域分析和系统频率响应分析奠定基础。

   • 系统理论中的应用：在线性时不变系统（LTI）理论中，$e^{-j\omega t}$ 是重要特征信号，输入它时输出是其倍数，这一性质在 LTI 系统分析（如频率响应计算）中起关键作用。

$e^{-j\omega t}$ 在信号处理中的应用

1. 频谱分析：

   实信号 $x(t)$ 可表示为

   $x(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }X(\omega )e^{j\omega t}d\omega$，

   其中频谱

   $X(\omega )={\int }_{-\infty }^{\infty }x(t)e^{-j\omega t}dt$

2. 正弦信号的复指数表示：

   $\cos ({\omega }_{0}t)=\frac{1}{2}(e^{j{\omega }_{0}t}+e^{-j{\omega }_{0}t})$，便于信号分析。

3. 调制解调应用：

   通信系统中，载波信号常用 $c(t)=e^{j{\omega }_{c}t}$ 表示，调制信号为 $s(t)c(t)$，解调时用 $e^{-j{\omega }_{c}t}$ 恢复原始信号。

4. 系统频率响应分析：

   对于 LTI 系统 $H$，其频率响应 $H(\omega )=|H(\omega )|e^{j\varphi (\omega )}$，输入为 $e^{j\omega t}$ 时，输出为 $y(t)=|H(\omega )|e^{j[\omega t+\varphi (\omega )]}$。

---

篇外：How do I check if $e^{j\omega t}$ is absolutely integrable?

机翻，未校。

asked：

asked Mar 4, 2017 at 21:20, JobHunter69

I’m trying to see if the Fourier transform of $e^{j\omega t}$ exists, so I am trying to evaluate this integral:

我在尝试判断 $e^{j\omega t}$ 的傅里叶变换是否存在，所以我在尝试计算这个积分：

${\int }_{-\infty }^{\infty }|e^{j\omega t}|$

but I am not getting anywhere and says nothing. How do I directly integrate this?

但我毫无进展，而且这个式子没有任何意义。我该如何直接积分？

$|{\int }_{-\infty }^{\infty }{e}^{j\omega t}|$

Also, just to confirm, its fourier transform doesn’t exist right?

另外，我想确认一下，它的傅里叶变换是不存在的，对吗？

Answer:

answered Mar 5, 2017 at 0:35, Mark Viola

The Fourier Transform of 1 is

1 的傅里叶变换是

F { 1 } ( ω ) = ∫ − ∞ ∞ ( 1 ) e j ω t   d t \mathscr{F}\{1\}(\omega)=\int_{-\infty}^\infty (1)e^{j\omega t}\,dt F{1}(ω)=∫−∞∞​(1)ejωtdt   (1)

As an improper Riemann integral or as a Lebesgue integral, the integral in (1) does not exist. However, interpreted as a Distribution, the Fourier Transform of 1 is

作为反常黎曼积分或勒贝格积分，式(1)中的积分并不存在。然而，如果将其解释为分布，1 的傅里叶变换是

F { 1 } ( ω ) = 2 π δ ( ω ) \mathscr{F}\{1\}(\omega)=2\pi \delta(\omega) F{1}(ω)=2πδ(ω)

where $\delta$ is the Dirac Delta, which is a distribution (or generalized function) and not a function.

其中 $\delta$ 是狄拉克德尔塔函数，它是一个分布（或广义函数），而不是一个普通函数。

---

via:

• 傅里叶变换的相关公式 $e^{j\omega t}$ 怎么化为三角函数 - CSDN 博客 月疯于 2018-06-04 17:02:21 发布
  https://blog.csdn.net/chehec2010/article/details/80569806

• 关于 $j\omega$ 和 $e^{j\omega t}$ 的领悟 - CSDN博客 xkf321 于 2017-05-05 10:27:54 发布
  https://blog.csdn.net/xkf321/article/details/71191823

• 复指数信号 $e^{j\omega t}$ 的图像及性质 - CSDN博客 山泼黛于 2021-10-26 16:53:16 发布
  https://blog.csdn.net/nebula1008/article/details/120974109

• 关于傅里叶变换的一些数学解释兼及其它。若 $f(x)$ 属于 $L^1$ 空间，它的傅里叶变换为什么不一定属于 $L^1$ 空间。 - CSDN博客 jiqiujia 于 2014-01-06 16:35:36 发布
  https://blog.csdn.net/zhulingchen/article/details/1793595

• integration - How do I check if $e^{j\omega t}$ is absolutely integrable? - Mathematics Stack Exchange
  https://math.stackexchange.com/questions/2172092/how-do-i-check-if-ejωt-is-absolutely-integrable