数据科学中的离散概率分布与连续概率分布

First lets define some terms for clarity

首先让我们定义一些术语以使其清晰

The sample space ΩThe sample space is the set of all possible outcomes of the experiment,usually denoted by Ω. For example, two successive coin tosses havea sample space of {hh, tt, ht, th}, where “h” denotes “heads” and “t”denotes “tails”.

样本空间Ω样本空间是实验所有可能结果的集合，通常以Ω表示。 例如，两个连续抛硬币的样本空间为{hh，tt，ht，th}，其中“ h”表示“头”，“ t”表示“尾”。

The event space AThe event space is the space of potential results of the experiment. Asubset A of the sample space Ω is in the event space A if at the endof the experiment we can observe whether a particular outcome ω ∈ Ωis in A. The event space A is obtained by considering the collection ofsubsets of Ω, and for discrete probability distributions (Section 6.2.1)A is often the power set of Ω.

事件空间A事件空间是实验潜在结果的空间。 如果在实验结束时可以观察到特定结果ω∈Ω是否在A中，则样本空间Ω的子集A在事件空间A中。通过考虑Ω子集的收集以及离散概率获得事件空间A分布(见第6.2.1节)A通常是Ω的功率集。

The probability PWith each event A ∈ A, we associate a number P (A) that measures theprobability or degree of belief that the event will occur. P (A) is calledthe probability of A.

概率P与每个事件A∈A相关联，我们将一个数字P(A)关联起来，该数字测量事件将发生的概率或信念程度。 P(A)称为A的概率。

The probability of a single event must lie in the interval [0, 1], and thetotal probability over all outcomes in the sample space Ω must be 1, i.e.,P (Ω) = 1. Given a probability space (Ω, A, P ), we want to use it to modelsome real-world phenomenon. In machine learning, we often avoid explic-itly referring to the probability space, but instead refer to probabilities onquantities of interest, which we denote by T as the target space and refer to elements of of T as states.

单个事件的概率必须位于区间[0，1]中，并且样本空间Ω中所有结果的总概率必须为1，即P(Ω)=1。给定概率空间(Ω，A， P)，我们想用它来模拟一些现实世界的现象。 在机器学习中，我们经常避免明确地提及概率空间，而代之以感兴趣的概率量，即以T表示目标空间 ，以T的元素表示状态。

The term probability relates is to an event and probability distribution relates is to a random variable.

术语probability与event ， probability distribution与random variable 。

It is a convention that the term probability mass function refers to the probability distribution of a discrete random variable and the term probability density function refers to the probability function of a continuous random variable.

按照惯例 ，术语probability mass function是指discrete random variable的probability distribution ，术语probability density function是指continuous random variable的概率函数。

了解概率密度 (Understanding Probability Density)

First a quick reference on PMF, PDF and CDF

首先快速了解PMF，PDF和CDF

In order to understand the heart of modern probability, we need to extend the concept of integration from basic calculus.To begin, let us consider the following piecewise function

为了理解现代概率的核心，我们需要从基本演算中扩展积分的概念。首先，让我们考虑以下分段函数

Applying the fundamental Riemann integration of Calculus we get

应用微积分的基本黎曼积分，我们得到

which has the usual interpretation as the area of the two rectangles that make up f (x).

通常将其解释为组成f(x)的两个矩形的面积。

The question is given f (x) = 1, what is the set of x values for which this is true? For our example, this is true whenever x ∈ (0, 1]. So now we have a correspondence between the values of the function (namely, 1 and 2) and the sets of x values for which this is true, namely, {(0, 1]} and {(1, 2]}, respectively. To compute the integral, we simply take the function values(i.e., 1,2) and some way of measuring the size of the corresponding interval.

给定问题f(x)= 1，这是真的x个值的集合是什么？ 对于我们的示例，每当x∈(0，1]时，这都是正确的。因此，现在我们在函数的值(即1和2)与x值的集合之间具有对应关系，即{ (0，1]}和{(1，2]}。要计算积分，我们只需简单地获取函数值(即1,2)，并采用某种方法测量相应区间的大小。

Since areas can be defined by definite integrals, we can also define the probability of an event occuring within an interval [a, b] by the definite integral

由于可以通过定积分来定义区域，因此我们也可以通过定积分来定义事件在[ a ， b ]区间内发生的概率

where f(x) is called the probability density function (pdf).

其中f ( x )称为概率密度函数(pdf)。

A function f(x) is called a probability density function if

函数f ( x )被称为概率密度函数，如果

1. f(x)≥0 for all x

   所有x的 f ( x )≥0

2. The area under the graph of f(x) over all the real line is exactly 1

   f ( x )图下所有实线的面积恰好是1

3. The probability that x is in the interval [a, b] is

   x在区间[ a ， b ]中的概率为

i.e. the area under the graph of f(x) from a to b.

即f ( x )从a到b的图下的面积。

In the problem above, the probability density function f(x) is called a uniform (flat) probability density function (pdf).

在上述问题中，概率密度函数f ( x )称为统一(平坦)概率密度函数(pdf) 。

So fundamentally, what does a probability density at point 𝒙 mean?

那么从根本上说，𝒙点的概率密度是什么意思？

Probability density function’s value at some specific point does not give you probability; it is a measure of how dense the distribution is around that value. It means how much probability is concentrated per unit length (d𝒙) near 𝒙, or how dense the probability is near 𝒙.

在某些特定点上的概率密度函数的值不会给您概率； 它衡量分布在该值附近的密度。 这意味着每单位长度(d𝒙)附近𝒙，或如何致密的概率是近𝒙多少概率浓缩。

For discrete random variables, we look up the value of a PMF at a single point to find its probability P(𝐗=𝒙) For continuous random variables, we take an integral of a PDF over a certain interval to find its probability that X will fall in that interval.

对于离散随机变量，我们在单个点上查找PMF的值以找到其概率P(𝐗=𝒙)对于连续随机变量，我们在一定间隔内对PDF进行积分以求出X的概率落在那个间隔。

离散随机变量 (Discrete Random Variable)

首先，什么是随机变量 (First what is a Random Variable)

Given a random experiment with sample space S,a random variable X is a set function that assigns one and only one real number to each element s that belongs in the sample space S.

给定一个具有样本空间S的随机实验， 随机变量 X是一个集合函数，它为属于样本空间S的每个元素s分配一个且仅一个实数。

The set of all possible values of the random variable X, denoted x, I am calling here as the support, or space, of X.

随机变量X的所有可能值的集合(表示为x)在这里称为X的支撑或空间 。

Note that the capital letters at the end of the alphabet, such as W,X,Y, and Z typically represent the definition of the random variable. The corresponding lowercase letters, such as w,x,y, and z, represent the random variable’s possible values.

请注意，字母末尾的大写字母(例如W，X，Y和Z)通常表示随机变量的定义。 相应的小写字母，例如w，x，y和z，代表随机变量的可能值。

现在什么是离散随机变量 (And now what is a Discrete Random Variable)

By a discrete random variable, it is meant a function (or a mapping), say X, from a sample space Ω, into the set of real numbers. Symbolically, if ω ∈Ω, then X (ω ) = x, where x is a real number.

离散随机变量是指从样本空间Ω到实数集的函数(或映射)，例如X。 象征性地，如果ω∈Ω，则X(ω)= x，其中x是实数。

A random variable X is a discrete random variable if:

在以下情况下，随机变量X是离散的随机变量 ：

• there are a finite number of possible outcomes of X, or
  X的可能结果数量有限，或者
• there are a countably infinite number of possible outcomes of X.
  X可能有无数的可能结果。

A countably infinite number of possible outcomes means that there is a one-to-one correspondence between the outcomes and the set of integers.

可能结果的数量无穷无尽意味着结果与整数集之间存在一一对应的关系。

No such one-to-one correspondence exists for an uncountably infinite number of possible outcomes.

对于无限数量的可能结果，不存在这样的一对一对应关系。

For a value x of the set of possible outcomes of the random variable X , i.e., x ∈ T , p(x) denotes the probability that random variable X has the outcome x.

对于随机变量X的可能结果集的值x，即x∈T，p(x)表示随机变量X具有结果x的概率。

For discrete random variables, this is written as P (X = x), which is known as the probability mass function. The pmf is often referred to as the distribution”. For continuous variables, p(x) is called the probability density function (often referred to as a density).

对于离散随机变量，它记为P(X = x)，称为概率质量函数。 pmf通常称为“分发”。 对于连续变量，p(x)称为概率密度函数(通常称为密度)。

When we say probability distribution it may pertain to a discrete random variable or a continuous random variable, depending on the context.

当我们说概率分布时，取决于上下文，它可能与离散随机变量或连续随机变量有关。

When the random variable is discrete, probability distribution means, how the total probability is distributed over various possible values of the random variable. Consider the experiment of tossing two unbiased coins simultaneously. Then, sample space S associated with this experiment is:

当随机变量是离散变量时，概率分布意味着总概率如何分布在随机变量的各种可能值上。 考虑一下同时扔两个无偏硬币的实验。 然后，与此实验相关联的样本空间S为：

S = {HH,HT,TH,TT} 

If we define a random variable X as: the number of heads on this sample space S, then we will have

如果我们将随机变量X定义为：该样本空间S上的磁头数，则我们将

X(HH)=2,

X ( HH )= 2，

X(HT)=X(TH)=1,

X ( HT )= X ( TH )= 1，

X(TT)=0

X ( TT )= 0

X(HH)=2,

X(HH)= 2，

X(HT)=X(TH)=1,

X(HT)= X(TH)= 1，

X(TT)=0.

X(TT)= 0。

The probability distribution of XX is then given by

X X的概率分布由下式给出

For a discrete random variable, we consider events of the type {X=x} and compute probabilities of such events to describe the distribution of the random variable.

对于离散随机变量，我们考虑{ X = x }类型的事件，并计算此类事件的概率以描述随机变量的分布。

The Probability Mass Function of a Discrete Random Variable expresses the probability of the variable being equal to each specific value in the range of all potential discrete values defi ned.The sum of these probabilities over all possible values equals 100%.

离散随机变量的概率质量函数表示变量在定义的所有潜在离散值范围内等于每个特定值的概率。在所有可能值上的这些概率之和等于100％。

In mathematical form, the probability that a discrete random variable X takes on a particular value x, that is, P(X=x), is frequently denoted f(x). The function f(x) is typically called the probability mass function

在数学形式上，离散随机变量X取特定值x(即P(X = x))的概率通常表示为f(x)。 函数f(x)通常称为概率质量函数

Let X be a discrete random variable with possible values denoted x1, x2, xi, x1, x2, xi,…. The probability mass function of X, denoted p

令X为离散随机变量，其可能值表示为x 1， x 2， xi ，x1，x2，xi等。 X的概率质量函数，表示为p

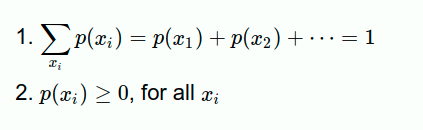
The same above in more general mathematical form, the probability mass function, P(X=x)=f(x), of a discrete random variable X is a function that satisfies the following properties:

上面的更一般的数学形式中，离散随机变量X的概率质量函数 P(X = x)= f(x)是满足以下性质的函数：

First item basically says that, for every element x in the support S, all of the probabilities must be positive. Note that if x does not belong in the support S, then f(x)=0. The second item basically says that if you add up the probabilities for all of the possible x values in the support S, then the sum must equal 1. And, the third item says to determine the probability associated with the event A, you just sum up the probabilities of the x values in A.

第一项基本上说，对于支撑S中的每个元素x，所有概率都必须为正。 注意，如果x不属于支撑S，则f(x)= 0。 第二项基本上说，如果将支撑S中所有可能的x值的概率加起来，则总和必须等于1。第三项表明要确定与事件A相关的概率，您只需求和求A中x值的概率。

Since f(x) is a function, it can be presented:

由于f(x)是一个函数，因此可以表示为：

• in tabular form
  以表格形式
• in graphical form
  以图形形式
• as a formula
  作为公式

离散随机变量的更多日常生活示例 (Some more daily life examples of discrete random variables)

If a random variable can take only a finite number of discrete values, then it isdiscrete.

如果随机变量只能采用有限数量的离散值，则它是离散的。

A fair die is a small cube with a natural number from 1 to 6 engraved on each side equally spaced without repetition. The fairness means that a die is made so that its weight is equally spread and, thus, all six faces are equally likely to face when rolled. So, if rolled, the set of numbers { 1,2,3,4,5,6} is the sample space of this experiment.

普通模具是一个小立方体，每侧刻有自然编号为1到6的等距间隔，没有重复。 公平性意味着模具的制造应使其重量均匀地分布，因此，在滚动时，所有六个面都可能相等。 因此，如果滚动，则数字集{1,2,3,4,5,6}是该实验的样本空间。

Now let’s consider the experiment of rolling a pair of fair dice. Then, the set ofpossible outcomes, that is, the sample space Ω, contains 36 pairs.

现在，让我们考虑掷出一对骰子的实验。 然后，可能的结果集(即样本空间Ω)包含36对。

In each pair, the first element represents the number appearing on one die and the second appearing on the other. We can define a discrete random variable X such that it assigns numbers 1 through 36 to the ordered pairs in Ω from the beginning to the end, respectively, as follows:

在每对中，第一个元素代表出现在一个骰子上的数字，第二个元素代表出现在另一个骰子上的数字。 我们可以定义一个离散随机变量X，以使其从头到尾分别以Ω的形式将数字1到36分配给有序对，如下所示：

Now an actual Python implemention in the below Jupyter Notebook

现在在下面的Jupyter Notebook中是一个实际的Python实现

连续随机变量 (Continuous Random Variables)

A continuous random variable differs from a discrete random variable in that it takes on an uncountably infinite number of possible outcomes.

连续随机变量与离散随机变量的不同之处在于，它承担了无限数量的可能结果。

While for a discrete random variable X that takes on a finite or countably infinite number of possible values, we determined P(X=x) for all of the possible values of X, and called it the probability mass function (“p.m.f.”). For continuous random variables, the probability that X takes on any particular value x is 0. That is, finding P(X=x) for a continuous random variable X is not going to work. Instead, we’ll need to find the probability that X falls in some interval (a,b), that is, we’ll need to find P(a<X<b). We’ll do that using a probability density function (“p.d.f.”).

对于具有有限或可计数的无限数量的可能值的离散随机变量 X，我们为X的所有可能值确定P(X = x)，并将其称为概率质量函数(“ pmf”)。 对于连续随机变量 ，X取任意特定值x的概率为0。也就是说，对于连续随机变量X求P(X = x)是行不通的。 相反，我们需要找到X落入某个间隔(a，b)的概率，也就是说，我们需要找到P(a <X <b)。 我们将使用概率密度函数(“ pdf”)进行此操作。

The Probability Density Function of a Continuous Random Variable expressesthe rate of change in the probability distribution over the range of potential continuous values defined, and expresses the relative likelihood of getting one value in comparison with another.

连续随机变量的概率密度函数表示在定义的潜在连续值范围内概率分布的变化率，并表示获得一个值与另一个值的相对可能性。

A nondiscrete random variable X is said to be absolutely continuous, or simply continuous, if its distribution function may be represented as

如果非离散随机变量X的分布函数可以表示为以下形式，则称其为绝对连续或简单连续的

where the function f (x) has the properties

函数f(x)具有属性

It follows from the above that if X is a continuous random variable, then the probability that X takes on any one particular value is zero, whereas the interval probability that X lies between two different values, say, a and b,is given by

由上可知，如果X是连续随机变量，则X取任意一个特定值的概率为零，而X位于两个不同值(例如a和b)之间的间隔概率由下式给出：

A function f (x) that satisfies the above requirements is called a probability function or probability distribution for a continuous random variable, but it is more often called a probability density function or simply density function. Any function f (x) satisfying Properties 1 and 2 above will automatically be a density function, and required probabilities can then be obtained from the more general form below

满足上述要求的函数f(x)称为连续随机变量的概率函数或概率分布，但通常称为概率密度函数或简称为密度函数。 满足以上属性1和2的任何函数f(x)将自动成为密度函数，然后可以从下面的更一般形式中获得所需的概率

概率密度函数 (Probability Density Function)

A function f : RD → R is called a probability density function (pdf ) if1. ∀x ∈ RD : f (x) > 02. Its integral exists and

函数f：RD→R称为概率密度函数(pdf)if1。 ∀x∈RD：f(x)> 02。

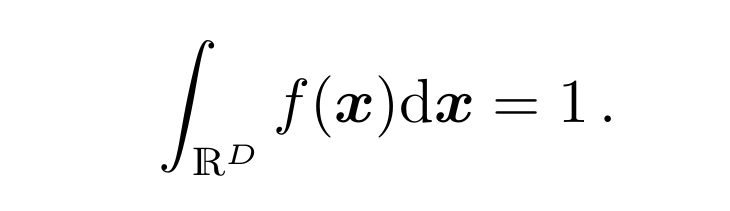
So observe that the probability density function is any function f that isnon-negative and integrates to one. And as stated above, we associate a random variable X with this function f by

因此，观察到概率密度函数是任何非负且积分为1的函数f。 如上所述，我们将一个随机变量X与该函数f相关联

As you can see, the definition for the p.d.f. of a continuous random variable differs from the definition for the p.m.f. of a discrete random variable by simply changing the summations that appeared in the discrete case to integrals in the continuous case.

如您所见，连续随机变量pdf的定义与离散随机变量pmf的定义不同，只需将离散情况下出现的总和更改为连续情况下的积分即可。

Now at the start of this article we discussed how density histogram (representing frequency) is defined so that the area of each rectangle equals the relative frequency of the corresponding class, and the area of the entire histogram equals 1. That suggests then that finding the probability that a continuous random variable X falls in some interval of values involves finding the area under the curve f(x) sandwiched by the endpoints of the interval.

现在，在本文开始处，我们讨论了如何定义密度直方图(代表频率)，以便每个矩形的面积等于相应类别的相对频率，而整个直方图的面积等于1。 连续随机变量X落入某个值区间的概率涉及找到曲线f(x)下由区间端点夹在中间的面积。

So from a large sample space of Pizza, the probability that a randomly selected Pizza weighs between 0.20 and 0.30 pounds is then this area: (which is what the definite Integral formulae above calculates )

因此，从大量的披萨样本空间中，随机选择的披萨重量在0.20到0.30磅之间的概率就是该区域：(这是上面的确定积分公式所计算出的)

Some examples of well known discrete probability distributions include:

众所周知的离散概率分布的一些示例包括：

• Poisson distribution.
  泊松分布。
• Bernoulli and binomial distributions.
  伯努利和二项分布。
• Multinoulli and multinomial distributions.
  多元分布和多项式分布。
• Discrete uniform distribution.
  离散均匀分布。
• The Geometric Distribution
  几何分布
• The Negative-Binomial Distribution
  负二项分布
• The Hypergeometric Distribution
  超几何分布

Some examples of common domains with well-known discrete probability distributions include:

具有众所周知的离散概率分布的常见域的一些示例包括：

• The probabilities of dice rolls form a discrete uniform distribution.
  掷骰的概率形成离散的均匀分布。
• The probabilities of coin flips form a Bernoulli distribution.
  掷硬币的概率形成伯努利分布。
• The probabilities car colors form a multinomial distribution.
  汽车概率形成多项式分布。

A quick summary

快速总结

Now lets see an simple actual exmaple of Discrete Probability Distribution. Quickly revisit the definition

现在让我们看一下离散概率分布的一个简单的实际例子。 快速重新定义

The probability distribution of a discrete random variable X is a list of each possible value of X together with the probability that X takes that value in one trial of the experiment.

离散随机变量 X 的 概率分布 为 X 的每个可能值的列表 一起与 X 取在实验中的一个试验，值 的概率 。

I start with a simple experiment, tossing a fair coin 10 times, and measured how many successes/heads I observe. I can use the number of successes (heads) observed in many ways to understand the basics of probability. For example, I could simply count how many times we see 0 heads, 1 head, 2 heads with our fair coin toss, and so on. Or here, I am just denoting the outcome with ‘H’ or ‘T’ for each experiment.

我从一个简单的实验开始，投掷一枚公平的硬币10次，并测量了我观察到的成功/头脑。 我可以使用以多种方式观察到的成功(正面)次数来了解概率的基础。 例如，我可以简单地算出我们抛硬币后看到0个头，1个头，2个头的次数，等等。 或者在这里，我只是为每个实验用“ H”或“ T”表示结果。

Now a quick and simple Math example of PDF

现在是一个简单快速的PDF数学示例

Let X be a continuous random variable whose probability density function is:

令X为连续随机变量，其概率密度函数为：

First, note again that

首先，请再次注意

For example,

例如，

which is clearly not a probability! In the continuous case, f(x) is instead the height of the curve at X=x, so that the total area under the curve is 1. In the continuous case, it is areas under the curve that define the probabilities.

这显然不是概率！ 在连续情况下，f(x)是X = x处曲线的高度，因此曲线下的总面积为1。在连续情况下，曲线下的面积定义了概率。

What is P(X=1/2)?

什么是P(X = 1/2)？

It is a straightforward integration to see that the probability is 0:

可以很容易地看到概率为0：

In general, if X is continuous, the probability that X takes on any specific value x is 0. That is, when X is continuous, P(X=x)=0 for all x in the support.

通常，如果X是连续的，则X取任意特定值x的概率为0。也就是说，当X连续时，支撑中所有x的P(X = x)= 0。

An implication of the fact that P(X=x)=0 for all x when X is continuous is that you can be less precise about the endpoints of intervals when finding probabilities of continuous random variables. That is:

当X是连续的时，所有x的P(X = x)= 0的事实是，当找到连续随机变量的概率时，间隔的端点可能不太精确。 那是：

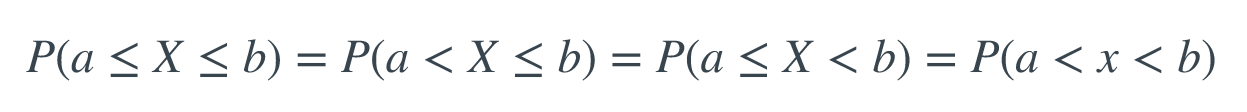
for any constants a and b.

对于任何常数a和b。

Further explanation of the above principle

上述原理的进一步说明

The probability of observing any single value of the continuous random variable is 0 since the number of possible outcomes of a continuous random variable is uncountable and infinite. That is, for a continuous random variable, we must calculate a probability over an interval rather than at a particular point. This is why the probability for a continuous random variable can be interpreted as an area under the curve on an interval. In other words, we cannot describe the probability distribution of a continuous random variable by giving probability of single values of the random variable as we did for a discrete random variable. This property can also be seen from the fact that

观察连续随机变量的任何单个值的可能性为0，因为连续随机变量的可能结果的数量是不可数且无限的。 也就是说，对于连续随机变量，我们必须计算一个区间而不是特定点的概率。 这就是为什么连续随机变量的概率可以解释为区间上曲线下方的面积的原因。 换句话说，我们不能像给出离散随机变量那样通过给出随机变量单个值的概率来描述连续随机变量的概率分布。 该属性还可以从以下事实看出：

for any real c

对于任何真实的c

为什么我需要在PDF上集成以获得概率 (Why do I need to Integrate over the PDF to get the Probaility)

In the case of of continuous random variable, we should not ask for the probability that X is exactly a single number (since that probability is zero). Instead, we need to think about the probability that x is close to a single number.

在连续随机变量的情况下，我们不应该要求X恰好是单个数字的概率(因为该概率为零)。 相反，我们需要考虑x接近单个数的可能性。

We capture the notion of being close to a number with a probability density function which is normally denoted by P(x). If the probability density around a point x is large, that means the random variable X is likely to be close to x. If, on the other hand, P(x)=0 in some interval, then X won’t be in that interval.

我们用概率密度函数 (通常用P(x)表示)接近数字。 如果点x周围的概率密度很大，则意味着随机变量X可能接近x 。 另一方面，如果在某个时间间隔内P(x)= 0 ，则X将不在该时间间隔内。

So building on the Integration concept of Calculus

因此，基于微积分的集成概念

If the probability of X being exactly at point 𝒙 is zero, how about an extremely small interval around the point 𝒙? Say, [𝒙, 𝒙+d𝒙]?

如果X恰好在𝒙处的概率为零，那么在around处的极小间隔又如何呢？ 说， [𝒙，𝒙+d𝒙]？

Let’s assume d𝒙 is infinitesimally small with a value of 0.00000000001.

假设d𝒙极小，值为0.00000000001。

Then the probability that X will fall in [𝒙, 𝒙+d𝒙] is the Area under the curve f(𝒙) sandwiched by [𝒙, 𝒙+d𝒙].

然后是X将落入[𝒙，𝒙+d𝒙]的概率是由[𝒙，𝒙+d𝒙]夹在曲线f(𝒙)下的面积 。

The Area Under a Curve — Integral Calculus Basics

曲线下的区域—积分演算基础

The area under a curve between two points can be found by doing a definite integral between the two points. To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b.

通过在两点之间进行定积分可以找到两点之间的曲线下面积。 要找到x = a和x = b之间的曲线y = f(x)下的面积，请在a和b的界限之间积分y = f(x)。

To translate the probability density P(x) into a probability, imagine that Ix is some small interval around the point x. Then, assuming P is continuous, the probability that X is in that interval will depend both on the density P(x) and the length of the interval

要将概率密度P(x)转换为概率，请假设Ix是围绕点x的某个小间隔。 然后，假设P是连续的，则X在该间隔中的概率将取决于密度P( x )和间隔的长度

 P ( X  ∈ Ix ) ≈ P ( x ) × Length of Ix 

We don’t have a true equality here, because the density P may vary over the interval Ix. But, the approximation becomes better and better as the interval Ix shrinks around the point x, as P will be come closer and closer to a constant inside that small interval. The probability P ( X ∈ Ix ) approaches zero as Ix shrinks down to an infinitesemally small value to the point x (consistent with our above result for single numbers), but the information about X is contained in the rate that this probability goes to zero as Ix shrinks.

这里我们没有真正的等式，因为密度P可能会在间隔Ix内变化。 但是，随着间隔Ix在点x周围缩小，逼近度会越来越好，因为P在该小间隔内将越来越接近常数。 当Ix缩小到点x的无穷小值时，概率P(X∈Ix)接近零(与我们对单个数的上述结果一致)，但是关于X的信息包含在该概率为零的比率中随着IX缩小。

So, to determine the probability that X is in any subset A of the real numbers, we simply add up the values of P(x) in the subset. By “add up,” we mean integrate the function P(x) over the set A.

因此，要确定X在实数的任何子集A中的概率，我们只需将子集中P(x)​​的值相加即可。 “累加”是指将函数P(x)集成到集合A上。

累积分布函数 (Cumulative Distribution Function)

The Cumulative Distribution Function of a Discrete Random Variable expresses the theoretical or observed probability of that variable being less than or equal to any given value. It equates to the sum of the probabilities of achieving that value and each successive lower value.

离散随机变量的累积分布函数表示该变量小于或等于任何给定值的理论或观察到的概率。 它等于达到该值的概率与每个后续较低值的总和 。

滚动单个模具的累积分布函数示例 (Example of the Cumulative Distribution Function for Rolling a Single Die)

And now the same for Continuous Random Variable

现在连续随机变量也一样

The Cumulative Distribution Function of a Continuous Random Variableexpresses the theoretical or observed probability of that variable being less than or equal to any given value. It equates to the area under the Probability Density Function curve to the left of the value in question.

连续随机变量的累积分布函数表示该变量小于或等于任何给定值的理论或观察到的概率。 它等于所讨论值左侧的“ 概率密度函数”曲线下的面积 。

Now implementing some very basic PDF with Python and Scipy

现在使用Python和Scipy实现一些非常基本的PDF

Another Jupyter Notebook to undersand how PDF is different from Probability

另一本Jupyter Notebook可了解PDF与概率的区别

翻译自: https://medium.com/@paulrohan/discrete-vs-continuous-probability-distributions-in-context-of-data-science-e48c7d40bc0f