数论入门符号_大符号入门指南第2部分

数论入门符号

Well hey there, Chef Remy! Welcome back to the kitchen!

好吧，雷米大厨！ 欢迎回到厨房！

Today we’re going to complete our intro to Big O Notation with O(log n), O(n log n), O(2^n) and O(n!) via an impeccable film, Pixar’s Ratatouille. When we last left off, we were preparing our famous ratatouille dish for notorious restaurant critic Anton Ego who was waiting patiently for his meal.

今天，我们将通过无可挑剔的电影皮克斯的《料理鼠王》完成关于O大符号的介绍，其中包括O(log n)，O(n log n)，O(2 ^ n)和O(n！)。 当我们最后一次离开时，我们正在为臭名昭著的餐厅评论家安东·埃戈(Anton Ego)准备我们着名的料理鼠王料理，他耐心地等待着他的饭菜。

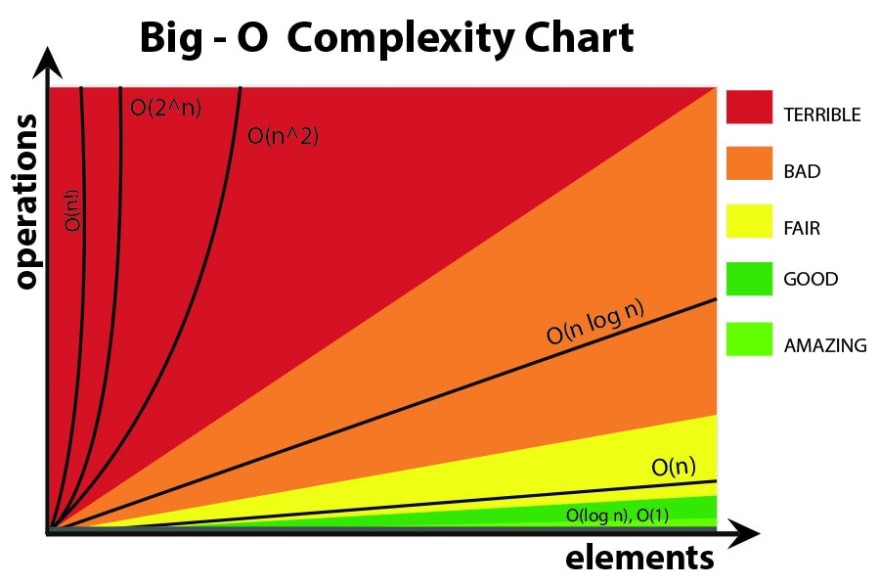
As a refresher, check out the time complexity comparison chart below:

复习一下下面的时间复杂度比较表：

O(log n)记录时间 (O(log n) Log Time)

Let’s say our waiter received an order from a mysteriously cloaked man (Chef Skinner in disguise! 🕵🏻‍♂️) who said “I’ll have what he’s having” in reference to Anton Ego.

假设我们的服务员收到了一个披着神秘衣服的男人的命令(伪装成厨师斯金纳！! ️)，他说“我将拥有他所拥有的”。

We know that Anton Ego is seated at table 29, so we will need to look up his food order through his table number. Lucky for us, the table numbers are always kept sorted in our array of orders. This is very helpful, because the restaurant is busy and we can’t keep the customers waiting! We need a quick way to figure out what Anton Ego ordered so that we can double it for the mysterious gentleman customer (coughSkinnercough):

我们知道Anton Ego坐在表29上，因此我们将需要通过他的表号查找他的食物订单。 对我们来说幸运的是，表号始终按照我们的orders数组进行排序。 这非常有帮助，因为餐厅很忙，我们不能让顾客等着！ 我们需要一种快速的方法来弄清楚Anton Ego订购了什么，以便为神秘的绅士客户( coughSkinnercough )加倍购买：

Since the orders are sorted by table number, we can use binary search to cut our search time down. In this method, we take the middle order in the orders array and check for three things:

由于订单是按table号排序的，因此我们可以使用二进制搜索来减少搜索时间。 在这种方法中，我们将orders数组中的中间订单作为对象并检查三件事：

• Does this table match the tableNum we’re looking for? If so, great! 🎉Return that order object. If not:

  该table是否与我们要查找的tableNum匹配？ 如果是这样，那就太好了！ 🎉返回该订单对象。 如果不：

• Is this table less than the tableNum that we’re looking for? If so, eliminate the first half of the array. If not:

  该table是否小于我们要查找的tableNum ？ 如果是这样，则消除阵列的前半部分。 如果不：

• Is this table greater than the tableNum that we’re looking for? If so, eliminate the second half of the array.

  该table是否大于我们要查找的tableNum ？ 如果是这样，请消除阵列的后半部分。

We repeat this process until we find the order object we’re looking for. Since we continuously eliminate half of the array with each recursive step, we say that the time complexity is O(log n) or log time.

我们重复此过程，直到找到所需的订单对象。 由于我们在每个递归步骤中都不断消除数组的一半，因此我们说时间复杂度为O(log n)或log time 。

This refers to a very math-y term, logarithm, which in Big O Notation looks at the question, “How many 2’s do we multiply together to get n?” If n was equal to 8, it would take 3 operations because 2 * 2 * 2 = 8. If n was 100, it would take 7 operations, and if n was 4,000,000,000 it would take only 32!(Grokking Algorithms)

这指的是一个非常数学的对数项，以Big O表示法着眼于以下问题：“我们将多少个2相乘以得到n ？” 如果n等于8，则将进行3次运算，因为2 * 2 * 2 =8。如果n为100，则将进行7次运算；如果n为4,000,000,000，则将仅进行32次运算( Grokking算法)。

This time complexity is super optimal, and just above O(1) constant time! If your solution is in O(log n) time, you should be pretty pleased! 🙌

这个时间复杂度是超最佳的，刚好超过O(1)恒定时间！ 如果您的解决方案是O(log n)时间，那么您应该会很高兴！ 🙌

O(n log n)线性时间 (O(n log n) Linearithmic Time)

Do you remember how in Part 1 of this Big O series, we wanted to sort the chopped vegetable slices in order to grab the best ones for Anton Ego’s meal? Last time we used a nested for loop which resulted in O(n²) time- not very optimal!

您是否还记得在本Big O系列文章的第1部分中，我们如何将切碎的蔬菜切片分类，以便为Anton Ego的餐点挑选最好的蔬菜切片？ 上次我们使用嵌套的for循环导致O(n²)时间-并不是非常理想！

Image credit: Pixar

图片来源：皮克斯

If we wanted to cut that time down (because Anton Ego is waiting and his review will make or break this restaurant!! ⏳), we could use the mergesort algorithm instead. Let’s pretend that each vegetable slice has a rating from 1–n, with 1 being the best slice and n being the worst:

如果我们想减少时间(因为Anton Ego正在等待，并且他的评论将决定这家餐厅的成立与否！ ⏳ )，我们可以改用mergesort算法。 假设每个蔬菜切片的等级为1–n，其中1为最佳切片，n为最差切片：

let zucchiniSlices = [20, 11, 25, 3, 14, 5,...]
                      
const merge = (arr1, arr2) => {
  let sorted = [];
  while (arr1.length && arr2.length) {
    if (arr1[0] < arr2[0]) {
      sorted.push(arr1.shift());
    } else { 
      sorted.push(arr2.shift());
    }
  };
  return sorted.concat(arr1.slice().concat(arr2.slice()));
};


const mergeSortByBestSlices = veggieSlices => {
  if (veggieSlices.length <= 1) return veggieSlices;
  let mid = Math.floor(veggieSlices.length / 2),
      left = mergeSortByBestSlices(veggieSlices.slice(0, mid)),
      right = mergeSortByBestSlices(veggieSlices.slice(mid));


  return merge(left, right);
};


mergeSortByBestSlices(zucchiniSlices) // [1, 2, 3, 4, 5, 6,...]

Mergesort uses a ‘divide and conquer’ approach (similar to binary search), taking an array and breaking it down continuously until each element becomes its own individual sub-array. Then it sorts those sub-arrays in pairs recursively until the entire array is sorted and joined back together again. This article does a great job of explaining the algorithm in further detail.

Mergesort使用“分而治之”的方法(类似于二进制搜索)，获取一个数组并将其连续分解，直到每个元素成为自己的单独子数组为止。 然后，它将这些子数组成对递归地排序，直到整个数组被排序并再次结合在一起。 本文在进一步详细解释该算法方面做得很好。

With this approach, the time complexity is O(n log n) because of the 2 main steps involved. The breakdown of the original zucchiniSlices array happens in O(log n) time. Building it back together through sorting requires O(n) time since each element (zucchini slice) must be considered, as well as O(log n) time to merge each sub-array back together. It’s like the equivalent of saying n * log n and it’s also known as linearithmic time.

使用这种方法，由于涉及两个主要步骤，因此时间复杂度为O(n log n) 。 原始zucchiniSlices数组的分解发生在O(log n)时间。 通过排序将其重新构建在一起需要O(n)时间，因为必须考虑每个元素(西葫芦切片)，还需要O(log n)时间来将每个子数组合并在一起。 这就像说n * log n ，也称为线性时间。

Since this sort method and time complexity is more optimal than O(n²), we can get those vegetables into the oven and onto Anton Ego’s plate much faster! 👍

由于这种排序方法和时间复杂度比O(n²)最佳，因此我们可以更快地将那些蔬菜放入烤箱并放在Anton Ego的盘子上！ 👍

O(2 ^ n)指数时间 (O(2^n) Exponential Time)

The ratatouille is almost ready to be served, but it feels like it’s missing… something. As Chef Remy, you look around and think of 3 herbs that might be a nice finishing touch to add on top: thyme, rosemary and/or marjoram 🌱.

料理鼠王几乎已经准备好送达了，但感觉好像缺少了……某物。 作为厨师雷米(Remy)，您环顾四周，想到3种草药，它们可能是添加在顶部的一种不错的点睛之笔：百里香，迷迭香和/或马郁兰🌱。

Thinking through the different combinations of herbs would yield O(2^n) possibilities:

通过对草药的不同组合进行思考将产生O(2 ^ n)可能性：

// with just 1 herb there are 2 options:
[""] or ["thyme"]// with 2 herbs there are 4 options:
[""] or ["thyme"] or ["rosemary"] or ["thyme", "rosemary"]// with 3 herbs there are 8 options:
[""] or ["thyme"] or ["rosemary"] or ["marjoram"] or
["thyme", "rosemary"] or ["thyme", "marjoram"] or ["rosemary", "marjoram"] or ["thyme", "rosemary", "marjoram"]

As we can see, the number of options grow in proportion to 2^n:

如我们所见，选项的数量与2 ^ n成正比：

• When n = 1, we have 2^1 possibilities.
  当n = 1时，我们有2 ^ 1个可能性。
• When n = 2, we have 2^2 possibilities.
  当n = 2时，我们有2 ^ 2的可能性。
• When n = 3, we have 2^3 possibilities, and so on.
  当n = 3时，我们有2 ^ 3个可能性，依此类推。

This is called a power set, where the goal is to find all possible subsets of the options given, and the time complexity can be costly. Luckily for Anton Ego, you instinctively know exactly what should be added (a sprig of rosemary of course! 👌) and won’t need to think about every combination. The dish is finally complete!

这称为功率集，其目标是找到给定选项的所有可能子集，并且时间复杂度可能很高。 幸运的是，对于Anton Ego，您本能地确切知道应该添加什么(当然是一小撮迷迭香！👌)，并且无需考虑每种组合。 这道菜终于完成了！

Voila!

瞧！

In general, you should do your best to avoid O(2^n) or exponential run times as they can blow up very quickly. This one is actually one of the worst time complexities, second only to O(n!).

通常，您应尽力避免O(2 ^ n)或指数运行时间，因为它们会很快爆炸。 实际上，这是最复杂的时间之一，仅次于O(n！)。

O(n！)阶乘时间 (O(n!) Factorial Time)

Being that tonight is the grand re-opening of our restaurant, the tables are packed and the servers are very busy running around to attend to each one!

今晚正是我们餐厅的隆重开幕，桌子已经排满，服务器非常忙碌，到处跑来跑去！

Image credit: Pixar

图片来源：皮克斯

Since time is of the essence and people are hungry, our waiter Linguini would like to calculate the best route between the tables so that he’ll walk (or skate) the minimum distance between each table. As it turns out, there are a LOT of possible routes between tables, even if there are only a few!

由于时间至关重要，而且人们很饿，因此我们的服务员Linguini希望计算桌子之间的最佳路线，以便他步行(或滑冰)每个桌子之间的最小距离。 事实证明，即使只有几个表，表之间也有很多可能的路由！

Possible serving routes between tables

表之间可能的服务路线

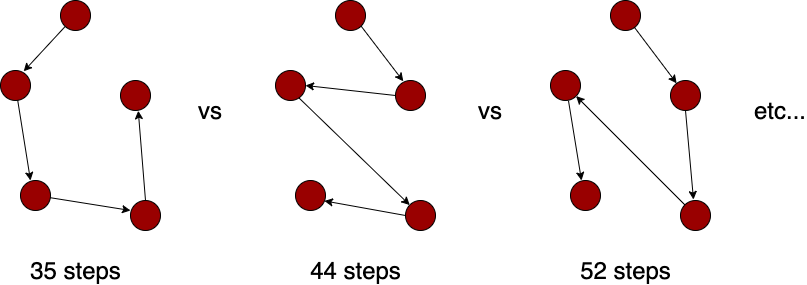
If Linguini is assigned to 5 tables, in order to examine each possible route you would need to do (5 * 4 * 3 * 2 * 1) permutations, which comes out to 120 in total. (Grokking Algorithms) If you were to add one more table to make 6, that would increase to 720 operations (6 * 120). If you add just one more to make 7 tables, that number goes up to 5,040, and if you somehow had 15 tables… that comes out to 1,307,674,368,000 operations! Yikes! 😱

如果将Linguini分配给5个表，则为了检查每条可能的路线，您需要进行(5 * 4 * 3 * 2 * 1)排列，总计为120。 ( Grokking算法)如果要再增加一张表来制作6，那将增加到720次运算(6 * 120)。 如果仅增加一个就可以创建7个表，那么这个数字将达到5,040，如果您以某种方式拥有15个表，那么结果就是1,307,674,368,000个操作！ kes！ 😱

This is the absolute worst of the Big O Notation values, known as O(n!) or factorial time. This time complexity should be avoided at all costs, and luckily it’s pretty rare in our day-to-day algorithms.

这是Big O表示法值的绝对最差值，称为O(n！)或阶乘时间。 应该不惜一切代价避免这种时间复杂性，幸运的是，在我们的日常算法中，这种情况非常罕见。

And there you have it! The culmination of our 2-part beginner’s guide to Big O Notation. (Feel free to check out part 1 here, covering O(1), O(n) and O(n²)!)

在那里，您拥有了！ 我们的两部分“大O符号”初学者指南达到了顶峰。 (在此处随意检查第1部分，涵盖O(1)，O(n)和O(n²)！)

So how did it go with the ratatouille? Seems as if they liked it. 😊

那么料理鼠王又如何呢？ 好像他们喜欢它。 😊

Image credit: Pixar

图片来源：皮克斯

翻译自: https://medium.com/swlh/a-beginners-guide-to-big-o-notation-part-2-c4ede76cea36

数论入门符号