优先级队列和堆_堆和优先级队列

最新推荐文章于 2024-06-22 09:02:14 发布

weixin_26746861

最新推荐文章于 2024-06-22 09:02:14 发布

阅读量528

点赞数

文章标签：队列 python java

原文链接：https://medium.com/swlh/heap-and-priority-queue-fbd41333dc0d

版权

优先级队列和堆

In this article you will learn all about Heap and Priority Queue | Data Structure

在本文中，您将了解有关堆和优先级队列的所有信息。数据结构

什么是堆？ (What is Heap ?)

A heap is a tree with some special properties. The basic requirement of a heap is that the value of a node must be ≥ (or ≤) than the values of its children. This is called heap property. A heap also has the additional property that all leaves should be at h or h — 1 levels (where h is the height of the tree) for some h > 0 (complete binary trees). That means heap should form a complete binary tree .

堆是具有某些特殊属性的树。堆的基本要求是节点的值必须大于或等于子节点的值。这称为堆属性。堆还具有附加属性，即对于某些h> 0(完整的二叉树)，所有叶子都应处于h或h — 1个级别(其中h是树的高度)。这意味着堆应该形成完整的二叉树。

堆的类型？ (Types of Heaps?)

Based on the property of a heap we can classify heaps into two types

根据堆的属性，我们可以将堆分为两种类型

Min heap: The value of a node must be less than or equal to the values of its children

最小堆：节点的值必须小于或等于其子节点的值

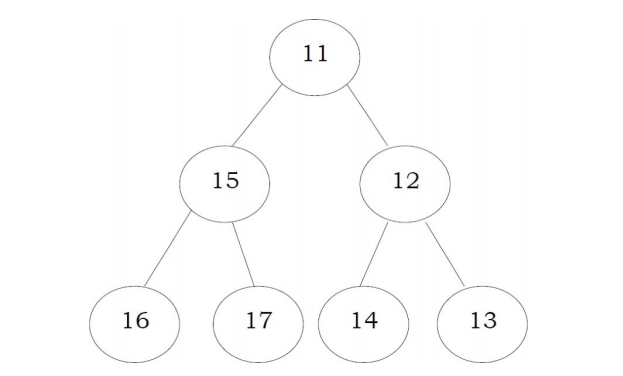
Max heap: The value of a node must be greater than or equal to the values of its children

最大堆：节点的值必须大于或等于其子节点的值

二进制堆 (Binary Heaps)

In binary heap each node may have up to two children. In practice, binary heaps are enough and we concentrate on binary min heaps and binary max heaps for the remaining discussion.

在二进制堆中，每个节点最多可以有两个子节点。实际上，二进制堆就足够了，在接下来的讨论中，我们将重点放在二进制最小堆和二进制最大堆上。

Before looking at heap operations, let us see how heaps can be represented. One possibility is using arrays. Since heaps are forming complete binary trees, there will not be any wastage of locations. For the discussion below let us assume that elements are stored in arrays, which starts at index 0. The previous max heap can be represented as:

乙 EFORE看着堆操作，让我们看到了堆如何来表示。一种可能是使用数组。由于堆正在形成完整的二叉树，因此不会浪费任何位置。对于下面的讨论，我们假设元素存储在数组中，数组从索引0开始。先前的最大堆可以表示为：

获取最大元素 (Getting the Maximum Element)

Since the maximum element in max heap is always at root, it will be stored at h→array[O].

由于最大堆中的最大元素始终位于根目录，因此将其存储在h→array [O]中。

Time Complexity: O(1).

时间复杂度：O(1)。

堆元素 (Heapifying an Element)

After inserting an element into heap, it may not satisfy the heap property. In that case we need to adjust the locations of the heap to make it heap again. This process is called heapifying. In maxheap, to heapify an element, we have to find the maximum of its children and swap it with the current element and continue this process until the heap property is satisfied at every node.

将元素插入堆后，它可能不满足堆属性。在这种情况下，我们需要调整堆的位置以使其再次成为堆。此过程称为堆化。在maxheap中，要堆集元素，我们必须找到其子元素的最大值并与当前元素交换它，然后继续此过程，直到每个节点上的heap属性都满足为止。

Note that : One important property of heap is that, if an element is not satisfying the heap property, then all the elements from that element to the root will have the same problem. In the example below, element 1 is not satisfying the heap property and its parent 31 is also having the issue. Similarly, if we heapify an element, then all the elements from that element to the root will also satisfy the heap property automatically. Let us go through an example. In the above heap, the element 1 is not satisfying the heap property. Let us try heapifying this element.

注意：堆的一个重要属性是，如果一个元素不满足堆属性，那么从该元素到根的所有元素都会有相同的问题。在下面的示例中，元素1不满足堆属性，并且其父级31也存在问题。同样，如果我们对一个元素进行堆放，那么从该元素到根的所有元素也将自动满足heap属性。让我们来看一个例子。在上述堆中，元素1不满足堆属性。让我们尝试堆砌此元素。

To heapify 1, find the maximum of its children and swap with that.

要堆1，请找到其最大子项并与其交换。

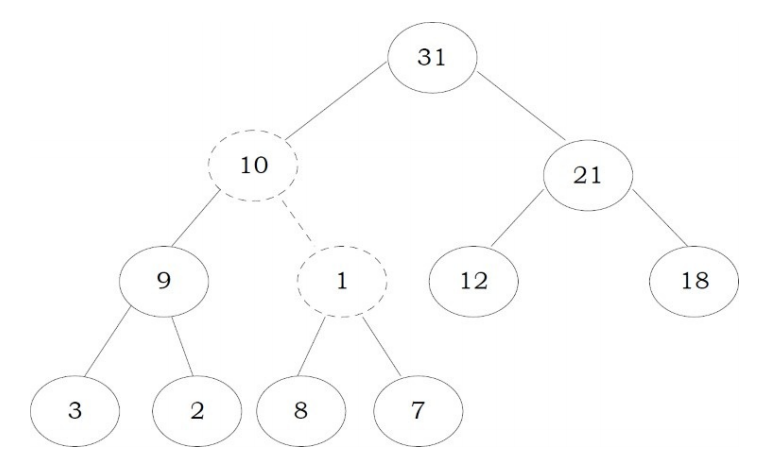
We need to continue this process until the element satisfies the heap properties. Now, swap 1 with 8.

我们需要继续此过程，直到元素满足堆属性为止。现在，将1与8交换。

Now the tree is satisfying the heap property. In the above heapifying process, since we are moving from top to bottom, this process is sometimes called percolate down. Similarly, if we start heapifying from any other node to root, we can that process percolate up as move from bottom to top.

现在，树满足了heap属性。在上面的堆积过程中，由于我们是从上到下移动的，因此有时将此过程称为向下渗透。同样，如果我们开始从其他任何节点到根进行堆扩，那么该过程可以随着从底部到顶部的移动而渗透。

Time Complexity: O(logn). Heap is a complete binary tree and in the worst case we start at the root and come down to the leaf. This is equal to the height of the complete binary tree. Space Complexity: O(1).

时间复杂度：O(logn)。堆是完整的二叉树，在最坏的情况下，我们从根开始，一直到叶。这等于完整的二叉树的高度。空间复杂度：O(1)。

class Heap :
    def heapify(self,arr,n,i):
        largest = i 
        left = 2 * i + 1
        right = 2 * i + 2
        
        if left < n and arr[i] < arr[left]:
            largest = left
        if right < n and arr[largest] < arr[right]:
            largest = right
        if largest != i:
            arr[i], arr[largest] = arr[largest],arr[i]
            self.heapify(arr,n,largest)
        
    def buildMaxHeap(self,arr,n):
        for i in range(n//2 , -1 , -1):
            self.heapify(arr,n,i)
            
            
arr = [1,4,2,6,7,3,5,3,2,7,4]
h = Heap()
h.buildMaxHeap(arr,len(arr))print(arr)

删除堆元素 (Deleting An Element for Heap)

The standard deletion operation on Heap is to delete the element present at the root node of the Heap. That is if it is a Max Heap, the standard deletion operation will delete the maximum element and if it is a Min heap, it will delete the minimum element.

堆上的标准删除操作是删除堆的根节点上存在的元素。也就是说，如果它是最大堆，则标准删除操作将删除最大元素，如果它是最小堆，则将删除最小元素。

Process of Deletion:Since deleting an element at any intermediary position in the heap can be costly, so we can simply replace the element to be deleted by the last element and delete the last element of the Heap.

删除过程 ：由于删除堆中任何中间位置的元素可能会很昂贵，因此我们可以简单地用最后一个元素替换要删除的元素，然后删除堆的最后一个元素。

Replace the root or element to be deleted by the last element.
用最后一个元素替换要删除的根或元素。
Delete the last element from the Heap.
从堆中删除最后一个元素。
Since, the last element is now placed at the position of the root node. So, it may not follow the heap property. Therefore, heapify the last node placed at the position of root.
从那以后，最后一个元素现在放置在根节点的位置。因此，它可能不遵循heap属性。因此，堆放放置在根位置的最后一个节点。

Note: Deleting an element uses PercolateDown, and inserting an element uses PercolateUp. Time Complexity: same as Heapify function and it is O(logn).

注意：删除元素使用PercolateDown，插入元素使用PercolateUp。时间复杂度：与Heapify函数相同，为O(logn)。

在堆中插入元素 (Inserting An Element in Heap)

Process of Insertion: Elements can be inserted to the heap following a similar approach as discussed above for deletion. The idea is to:

插入过程 ：可以按照上面讨论的用于删除的类似方法将元素插入到堆中。这个想法是：

First increase the heap size by 1, so that it can store the new element.
首先将堆大小增加1，以便它可以存储新元素。
Insert the new element at the end of the Heap.
在堆的末尾插入新元素。
This newly inserted element may distort the properties of Heap for its parents. So, in order to keep the properties of Heap, heapify this newly inserted element following a bottom-up approach.
这个新插入的元素可能会扭曲其父元素的堆属性。因此，为了保留Heap的属性，请按照自下而上的方法堆放此新插入的元素。

Time Complexity: O(logn). The explanation is the same as that of the Heapify function.

时间复杂度：O(logn)。说明与Heapify函数相同。

堆排序 (Heap Sort)

One main application of heap ADT is sorting (heap sort). The heap sort algorithm inserts all elements (from an unsorted array) into a heap, then removes them from the root of a heap until the heap is empty. Note that heap sort can be done in place with the array to be sorted. Instead of deleting an element, exchange the first element (maximum) with the last element and reduce the heap size (array size). Then, we heapify the first element. Continue this process until the number of remaining elements is one.

堆ADT的一项主要应用是排序(堆排序)。堆排序算法将所有元素(从未排序的数组中)插入到堆中，然后从堆根中删除它们，直到堆为空。请注意，堆排序可以在要排序的数组中进行。与其删除元素，不如将第一个元素(最大)与最后一个元素交换，并减小堆大小(数组大小)。然后，我们堆化第一个元素。继续此过程，直到剩余元素数为1。

    def heapsort(self, arr):
        n = len(arr)
        self.buildMaxHeap(arr, n)
        for i in range(n-1, 0, -1):
            arr[i], arr[0] = arr[0], arr[i]
            self.heapify(arr, i, 0)arr = [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]
h = Heap()
h.heapsort(arr)
print(arr)

优先队列 (Priority Queue)

In some situations we may need to find the minimum/maximum element among a collection of elements. We can do this with the help of Priority Queue ADT. A priority queue ADT is a data structure that supports the operations Insert and DeleteMin (which returns and removes the minimum element) or DeleteMax (which returns and removes the maximum element).

在某些情况下，我们可能需要在元素集合中找到最小/最大元素。我们可以借助Priority Queue ADT来做到这一点。优先级队列ADT是支持操作Insert和DeleteMin(返回并删除最小元素)或DeleteMax(返回并删除最大元素)的数据结构。

These operations are equivalent to EnQueue and DeQueue operations of a queue. The difference is that, in priority queues, the order in which the elements enter the queue may not be the same in which they were processed. An example application of a priority queue is job scheduling, which is prioritized instead of serving in first come first serve.

这些操作等效于队列的EnQueue和DeQueue操作。区别在于，在优先级队列中，元素进入队列的顺序可能与处理它们的顺序不同。优先级队列的一个示例应用是作业调度，该作业调度具有优先级，而不是先来先服务。

A priority queue is called an ascending — priority queue, if the item with the smallest key has the highest priority (that means, delete the smallest element always). Similarly, a priority queue is said to be a descending –priority queue if the item with the largest key has the highest priority (delete the maximum element always). Since these two types are symmetric we will be concentrating on one of them: ascending-priority queue.

如果具有最小键的项具有最高优先级(即始终删除最小元素)，则优先级队列称为升序-优先级队列。同样，如果密钥最大的项具有最高优先级(始终删除最大元素)，则优先级队列被称为降序-优先级队列。由于这两种类型是对称的，因此我们将集中讨论其中一种：升序优先队列。