三阶行列式简便算法_关于线性代数三阶行列式运算法则的推导（一）

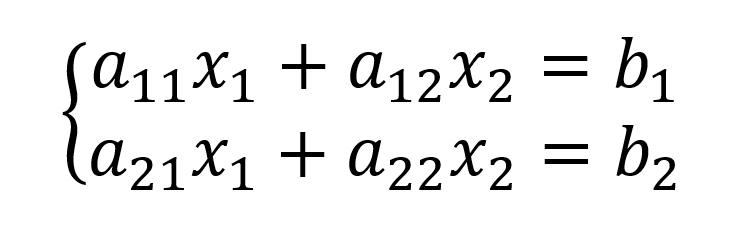
对于线性代数的初学者来说，相信在看完二阶行列式后很清楚的明白二阶行列式可以来解二元一次方程组。

考虑到每篇文章的篇幅问题，如果过于长我相信各位都会比较没有耐心吧。

所以此篇文章分为三部分：

1. 线性代数三阶行列式的运算法则推导引入篇（一）——二元一次方程的解法（详细）
2. 线性代数三阶行列式的运算法则推导证明篇（二）——三元一次方程的解法（详细）
3. 线性代数三阶行列式的运算法则推导结论篇（三）——三元一次方程的解法得出三阶行列式运算法则（定义运算法则详细，其余在第二篇中证明的简洁带过）

二元一次方程组

对于上面的方程组的解法其实是通过消元，消去一式和二式的相同部分，然后就可以解出方程的解（当方程组有解的情况下）。

来解这个方程组，首先在我默认是消除

,我相信每个人都同意吧。

由第一式乘以

的系数得:

·······①

而如果要消除

,那么第二式就需要乘以

得系数得：

·······②

观察上述得式子便可以发现

前面有相同得系数，那么我们令①减去②，便可得：

那么便可得

得值：

观察式子可以发现，其实关于方程得解只和系数有关（当方程有解时），那么其实可以把其对应得系数按照2×2来写出。

二阶行列式

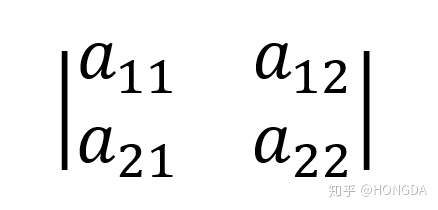
发现这个写法得到的算法是

而

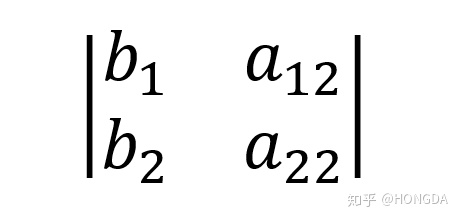
便可得：

刚刚好为关于

得解的除数的上半部分。

那么这个新运算便刚刚好完全符合两个式子。

对于上半部分，也就是

的解，用

分别替代原本的

就可以得到。

同理，对于另一个未知数，就是拿

分别替换原本的

而分母不变。

我们尝试着用矩阵表示出方程的解。

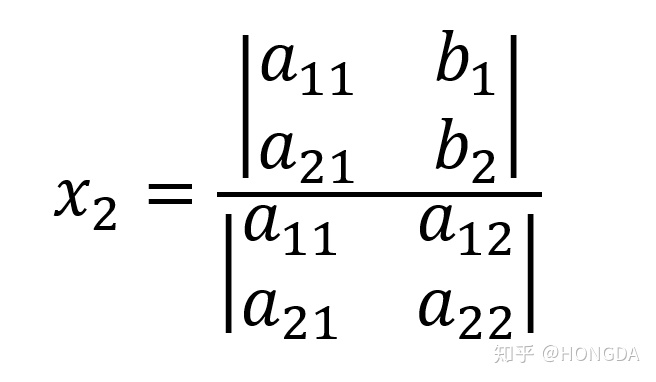
这样看起来就简洁很多。

同时也得出一个运算法则

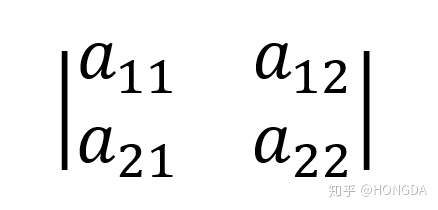
对于上面的二阶行列式的运算为：

本篇完。

HONGDA：关于线性代数三阶行列式运算法则的推导（二）​zhuanlan.zhihu.com