向量的内积也叫向量的数量积、点积。我们定义两个向量的内积是一个数:
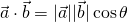
其中  是这两个向量的夹角。
是这两个向量的夹角。
对于向量的内积,最重要的一个结论是:
定理1:两向量垂直的充分必要条件是它们的内积为 0,即

这个定理我们几乎不用证明了,因为从定义来看,如果两个向量都不零向量,则只能是夹角  。而零向量的方向是任意的,零向量与任垂直何向量都垂直。
。而零向量的方向是任意的,零向量与任垂直何向量都垂直。
坐标下的内积:如果
向量的内积也叫向量的数量积、点积。我们定义两个向量的内积是一个数:
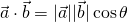
其中  是这两个向量的夹角。
是这两个向量的夹角。
对于向量的内积,最重要的一个结论是:
定理1:两向量垂直的充分必要条件是它们的内积为 0,即

这个定理我们几乎不用证明了,因为从定义来看,如果两个向量都不零向量,则只能是夹角  。而零向量的方向是任意的,零向量与任垂直何向量都垂直。
。而零向量的方向是任意的,零向量与任垂直何向量都垂直。
坐标下的内积:如果

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


