交叉(Crossover)
在上一篇文章所描述的选择过后,我们在一个population中选出了一部分可以用作交配的父母个体,而染色体交叉操作,就是指我们在这些父母个体中,选择两个进行相互交配,将他们的染色体按照某种方式相互交换部分基因,形成两个新的个体的过程。
实际上交叉操作还分为无性、有性、多亲重组三种:
- 无性:子代由一个父个体产生
- 有性:子代由两个父个体产生一个/两个子个体
- 多亲重组:多余两个父个体产生一个/多个子个体
适用于二进制编码的交叉算子:
- 单点交叉(One-point Crossover):指在个体编码串中只随机设置一个交叉点,将染色体分成两部分,子代染色体的左右两侧分别来自于父母染色体。

- 两点交叉/多点交叉(Two-point/Multi-point Crossover):在个体编码串中随机设置了两个/多个交叉点,然后再以间隔交换的方式进行部分基因交换。

- 均匀交叉(也称一致交叉,Uniform Crossover):两个配对个体的每个基因座上的基因都以相同的交叉概率进行交换,从而形成两个新个体。
适用于浮点数/实数编码的交叉算子:
- 离散重组:子个体的每一个变量按照等概率随机地挑选父母个体的变量值,组成新的子个体。
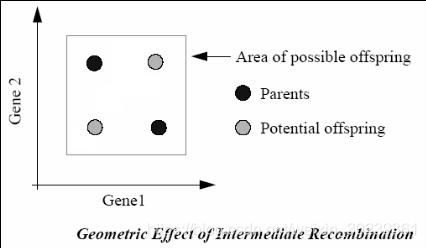
- 中间重组:
V a r s o n = V a r f a t h e r 1 + α × ( V a r f a t h e r 2 − V a r f a t h e r 1 ) Var_{son}=Var_{father1}+\alpha×(Var_{father2}-Var_{father1}) Varson=Varfather1+α×(Varfather2−Varfather1),其中 α \alpha α是比例因子,由[-d,1+d]上均匀分布地随机数产生。d=0时,为中间充足,一般d=0.25。重组时,先为每一个子代的每一个变量产生一个 α \alpha α。


- 线性重组:其实就是中间重组的一个特殊情况,对于同一个子代,它的每一个变量的比例因子
α
\alpha
α都是固定的。

模拟二进制交叉SBX(Simulated Binary Crossover)
SBX方法的主要思想是在使用浮点数编码/实数编码时,可以模拟二进制编码的交叉操作:

原论文:
Agrawal R B , Deb K , Agrawal R B . Simulated Binary Crossover for Continuous Search Space[J]. Complex Systems, 2000, 9(3):115-148.
混合交叉算子BLX(the Blend Crossover operator)

原论文:
Eshelman L J, Schaffer J D. Real-coded genetic algorithms and interval-schemata[M]//Foundations of genetic algorithms. Elsevier, 1993, 2: 187-202.
关于交叉操作有些优秀的博文推荐阅读:
遗传算法中几种交叉算子小结
Simulated Binary Crossover(SBX)的学习
SBX(Simulated binary crossover)模拟二进制交叉算子和DE(differential evolution)差分进化算子
百度文库-遗传算法
变异(Mutation)
在交叉操作过后形成的新个体,有一定的概率会发生基因变异,与选择操作一样,这个操作是基于概率的,这个概率成为变异概率 p m p_m pm。一般来说变异概率设置得很小,一般 p m ≤ 0.05 p_m≤0.05 pm≤0.05。
适用于二进制编码和实数编码的变异算子:
最简单的做法就是:对交叉后代集中每个后代的每一位,产生一个随机数
r
⊂
[
0
,
1
]
r\subset[0,1]
r⊂[0,1],若
r
≤
p
m
r≤p_m
r≤pm则将该位取反,否者该位不变。
- 基本位变异(Simple Mutation):对个体编码串中以变异概率、随机指定的某一位或某几位仅因座上的值做变异运算。
- 均匀变异(Uniform Mutation):分别用符合某一范围内均匀分布的随机数,以某一较小的概率来替换个体编码串中各个基因座上的原有基因值。(特别适用于在算法的初级运行阶段)
- 边界变异(Boundary Mutation):随机的取基因座上的两个对应边界基因值之一去替代原有基因值。特别适用于最优点位于或接近于可行解的边界时的一类问题。
- 非均匀变异:对原有的基因值做一随机扰动,以扰动后的结果作为变异后的新基因值。对每个基因座都以相同的概率进行变异运算之后,相当于整个解向量在解空间中作了一次轻微的变动。
- 高斯近似变异:进行变异操作时用符号均值为P的平均值,方差为P**2的正态分布的一个随机数来替换原有的基因值。
另外:
如果变异概率很大,那么整个搜索过程就退化为一个随机搜索过程。所以,比较稳妥的做法是,进化过程刚刚开始的时候,取p为一个比较大的概率,随着搜索过程的进行,p逐渐缩小到0附近。
关于变异操作有些优秀的博文推荐阅读:
遗传算法系列 (4) 变异算法
【建模必备】遗传算法的基本原理与步骤(变异)
百度文库-遗传算法
替换策略
除了父子个体的选择、重组、变异之外,还需要考虑的是替换策略——生成的新个体如何取代旧的个体。
有如下几种:
- 如果生成一个子个体,可以用来替换掉最差的父个体。这个替换规则可以(或必须)基于子个体的适应度优于父个体。
- 玻尔兹曼(Boltzmann)选择可以用来确定子个体是否替换父个体。
- 新的子个体替换掉种群中的劣势个体。
























 21万+
21万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








