对圆柱面的曲面积分_曲面之二-曲面的第一、第二基本形式

古典微分几何一般都是从曲线开始，之前的一些文章基本上也算涵盖了曲线论比较基础的内容。曲线的学习思路一般是这样的：

那么对于曲面其实我们也可以采取类似的思路，当然由于曲面与曲线的不同之处所以在整个线路上也有不同的地方：

切平面

鉴于我们已知了曲线的切向量，那么我们就从曲面上的曲线开始吧，曲面 S 上的曲线 C 可写成：

图片来自 《微分几何》

对于曲面上的一点

，有

， 在

中曲线的坐标为：

C 在

的切向量为：

当然其实我应该写成：

处切向量形式为：

同样我们也能说明当向量形式为

, 这一定存在某曲线 C， 并且 这个向量是过

的此向量的切向量。

曲面 S 上所有过

点的曲线的切向量构成一个二维线性空间。

我们称这个二维线性空间为曲面 S 在

点的切平面，记为

, 切平面

中的向量称为曲面在

点的切向量，

是

的一组基。

切平面的定义出来之后，法向量的定义也随之而出：

图片来自 《微分几何》

法向量

虽然

和

均与 切平面垂直，但一般我们会定义单位法向量为：

参数变换

容易想象，正如参数曲线，针对参数曲面，我们也可以选取不同的参数。这也并不影响在 P 点的切向量和法向量。

这里给出简单的证明，假设曲面

选取另一套参数，也就是

, 当然这样的变换同样需要是一对一，那么需要做到 雅可比矩阵 不为0， 也就是：

根据链式法则：

我们可以写下：

也就是：

其实这里已经能说明问题了，那就是

是在

的 span 上，再加上都过 P 点，那就是同样的平面和会有同样的法向量。

当然我也可以叉乘来看：

注意这里：

所以也有看到写成：

当然结论也是一样，那就是

在参数变换下曲面的切平面、法向量不变。

度量 - 第一基本形式

解决掉 切平面、法向量、参数变换 之后，我们开始来研究度量问题。度量是我们想要解决比如 长度、角度、面积 等问题。

那么在

中，我们是如何来计算这些问题的呢？

内积。

给定的向量

,它们的内积形式是：

• 长度

• 角度

• 面积

可能在多元微积分中我们也处理过比如 曲线长度、曲面面积 等问题，用积分来解决问题：

其关键思想还是以直代弯，所以当我们考察曲面的时候，需要考察是的 切平面

上的向量：

图片来自《微分几何》

以下就直接引用 wikipedia 了 o(╯□╰)o:

在微分几何中，第一基本形式（first fundamental form）是三维欧几里得空间中一个曲面的切空间中内积，由

中标准点积诱导。它使得曲面的曲率和度量性质（比如长度与面积）可与环绕空间一致地计算。第一基本形式用罗马数字 I 表示：

设 X(u, v) 是一个参数曲面，则两个切向量的内积为

这里 E, F,与 G 是第一基本形式的系数。
第一基本形式可以表示为一个对称矩阵

第一基本形式完全描述了曲面的度量性质。从而，它使我们可以计算曲面上曲线的长度与区域的面积。线元素（line element）可以用第一基本形式的系数表示为：

由

给出的经典面积元素可以用第一基本形式的系数利用拉格朗日恒等式（Lagrange's identity）写出，

或者写成更相符

的形式：

• 线素：

其中：

• 弧长

曲面上的曲线弧长

面积

曲面上曲线切向量的夹角太繁琐了，此处略去。

我们把仅仅用 E， F， G 表示出来的几何量称为内蕴量，如弧长、交角、面积等。讨论这些量的几何学就称为曲面的内蕴几何学，由这些内蕴量所决定的几何性质称为曲面的内蕴性质。

有 E, F, G， 我们无需知道这个曲面映射的具体形式：

就可以求一些值，也就可以某种程度的研究曲面。我们并不关心这个曲面是如何嵌入在

中的。

等距对应

如果两个曲面：

在参数 (u, v) 和 参数

的一一对应下，它们的第一基本形式相等：

则称这两个曲面是等距的，且称 (u, v) 和

之间的对应为等距对应。

在数学中，“等距同构”或称“保距映射”（isometry、简称等距），是指在度量空间之中保持距离不变的同构关系。几何学中的对应概念是全等变换。

• 平面 vs 圆柱面

平面

计算：

平面的第一基本形式：

圆柱面

计算：

圆柱面的第一基本形式：

可见 平面 与 圆柱面 的第一基本形式是一样的。这两个曲面是同构的，最直观的理解就是我可以把 一张纸 卷成 圆柱，也可以把 圆柱 展开成一张纸。

图片来自wikipedia

• 悬链面 vs 正螺旋面

悬链面

图片来自wikipedia

悬链曲面（又名悬垂曲面）是一个曲面，是将悬链线绕其准线旋转而得，故为一旋转曲面。除了平面以外，悬链曲面也是第一个被发现的极小曲面，在1744年被莱昂哈德·欧拉发现且证明。

更多关于悬链线，可以了解一下 伯努利 家族以及变分法的故事，o(╯□╰)o

正螺旋面：

图片来自wikipedia

它们的第一基本形式相同（计算略去）

螺旋曲面和悬链曲面是局部等距的曲面。 gif 展示它们之间的变换：

图片来自wikipedia

共形对应

如果两个曲面：

的参数 参数 (u, v) 和 参数

之间建立了一一对应：

后，它们的第一基本形式

成比例：

其中

, 则称这两个曲面是共形的，且称 (1) 式为共形对应。

可以看出来

在

的切向量关于

的分量在共形对应下，

处相应的切向量关于

的分量相同。

可以进一步证明如果在

有两个切向量

, 那么在共形对应下,

有相应的切向量

, 可以容易证明：

所以共形对应又称保角对应。

数学上，共形变换（英语：Conformal map）或称保角变换，来自于流体力学和几何学的概念，是一个保持角度不变的映射。 更正式的说，一个映射

称为在

共形(或者保角)，如果它保持穿过

的曲线间的定向角度，以及它们的取向也就是说方向。共形变换保持了角度以及无穷小物体的形状，但是不一定保持它们的尺寸。

共形的性质可以用坐标变换的导数矩阵雅可比矩阵的术语来表述。如果变换的雅可比矩阵处处都是一个标量乘以一个旋转矩阵，则变换是共形的。

图片来自wikipedia

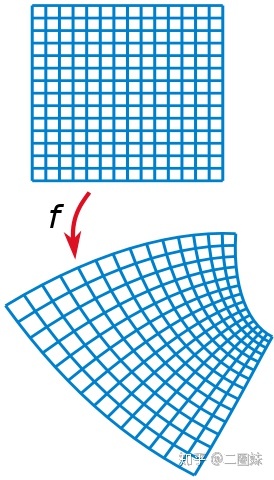
任何曲面必于平面共形对应

对任何曲面

，总能选到一族新的参数

, 使得第一基本形式为

称这种参数 (u, v) 为等温参数。

以上其实某种程度是绘制世界地图的数学基础。 →

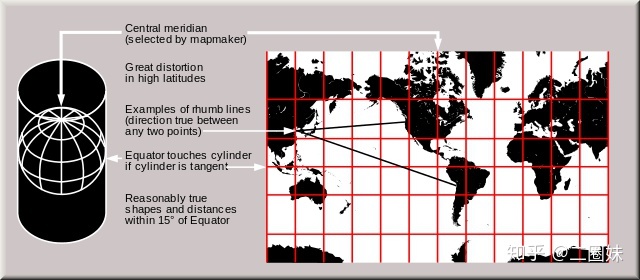
• 墨卡托投影

常见的世界地图绘制 墨卡托投影 是一种等角投影。

图片来自wikipedia

• 球极平面投影

球极平面投影 也是一种常见的绘制地图的 等角投影。

图片来自wikipedia

曲面的第二基本形式

图片来自《微分几何》

第二基本形式关心的是曲面在某处的弯曲程度 - 一个简单的衡量是曲面上邻近的点与切平面的距离，比如上图中曲面上的

到 P 点的切平面

的垂直距离

.

利用泰勒展开：

有：

为法向量，所以前两项为0，略去的部分是三阶及之上的小量，有：

当然可以 大于0和小于0，分别在

的两侧

以下二次微分形式 我们称为曲面的第二基本形式：

我们还可以利用：

于是

也可以写成：

也可以继续利用

继续展开。此处不再继续。

参考：

• 《微分几何》
• wikipedia