提示:本文的适用对象为已修过《微积分A1》的非数学系学生,文中题型方法为个人总结,为个人复习使用。部分理解虽然不太严谨,但对于解题的实用性较强。若有疏漏or错误,欢迎批评指正。
一、关于第一型曲线积分与第一型曲面积分
对于已经熟知第一型曲线积分和第一型曲面积分定义的朋友们来说,我在这里主要提出五个问题,以帮助大家的理解和做题。
Q1:第一型曲线/曲面积分与重积分的区别
重积分是在某一个区域内进行积分,是“不等关系”;而曲线/曲面积分是在某一条线/某一个平面上进行积分,是“等号关系”。
Q2:曲线的弧长与曲面的面积
关于微元产生的原因,详见《高等微积分教材(下)》的3.5节等多个部分,此处对不同形式曲线曲面微元的形式进行了整理
首先是曲线的弧长(对于光滑的正则曲线而言)
1、以参数方程表示的形式:
存在以下形式:
其中,上式表示的是空间曲线;下面表示平面








 本文针对已掌握微积分基础的非数学专业学生,探讨第一型曲线积分与第一型曲面积分的区别及计算方法,包括弧长与面积的微元表达式,同时阐述了重积分与曲线积分的本质差异。此外,讲解了第二型曲线积分的概念,并介绍了格林公式及其应用,包括曲线积分与路径无关的条件。文章强调了在实际解题中确定积分范围的技巧以及使用格林公式时的注意事项。
本文针对已掌握微积分基础的非数学专业学生,探讨第一型曲线积分与第一型曲面积分的区别及计算方法,包括弧长与面积的微元表达式,同时阐述了重积分与曲线积分的本质差异。此外,讲解了第二型曲线积分的概念,并介绍了格林公式及其应用,包括曲线积分与路径无关的条件。文章强调了在实际解题中确定积分范围的技巧以及使用格林公式时的注意事项。
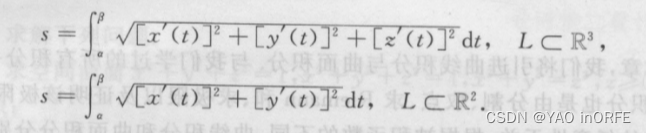
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








