曲线绕x轴旋转曲面方程_偏微分 | 热传导方程与Laplace方程

弄清方向导数是什么？

全微分：https://www.zhihu.com/question/31464934/answer/152231899

偏导数、全导数：什么是全导数？

方向导数、梯度：https://www.zhihu.com/question/36301367/answer/156102040

（自己看的）

(x,y)的导数：过点(x,y)的切线斜率（y变化率）

微分：dy=f'(x0)dx，y随x离开x0变化的变化量，过点(x,y)的切线。x0 = x时指代任一x点

(x,y)的偏导：（三维）固定y/x，拍扁到x/y轴上曲线过点(x,y)的切线斜率。z的变化率

(x,y)的方向导数：（三维）拍扁到某方向上，过点(x,y)的曲线上过点(x,y)的切线斜率。z的变化率。偏导数就是在x轴方向/y轴方向

(x,y)全微分：dz = z_x(x)dx + z_y(y)dy 从点(x,y)出发的dz（变化量）。过点(x,y)的切平面

点(x,y)在任意方向上都可以做出过该点在且在曲面z上的曲线

故可以对每条曲线均做过(x,y)的切线

梯度：一个矢量，在这个方向上的方向导数最大。大小正好是该最大方向上的方向导数。（增长最快的方向）

---

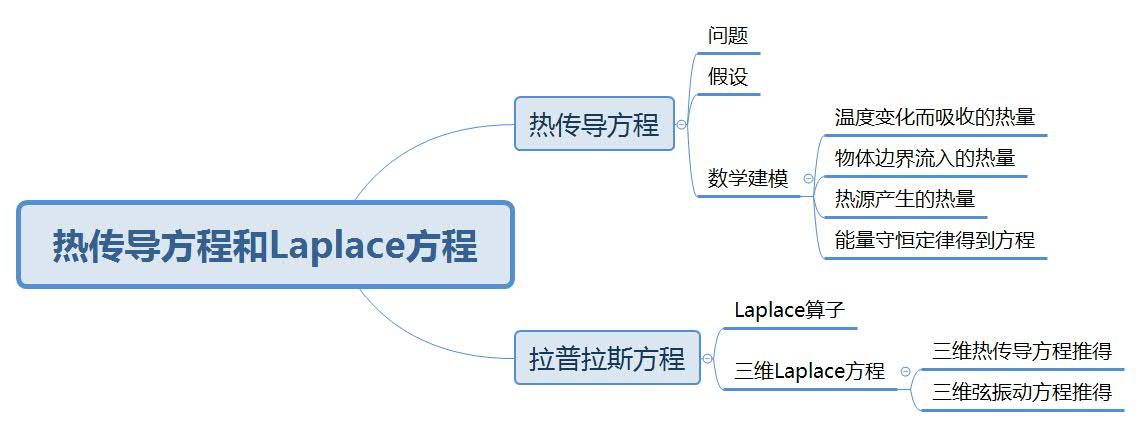
热传导方程

问题：

在三维空间中，求某一物体内部温度的分布和变化规律。

假设：

• 物体均匀、各向同性
• 物体内部有热源，且与周围介质有热交换

数学建模：

• 能量守恒定律：因温度变化吸收的热量 = 物体边界流入的热量+物体内部热源生成的热量
• 傅里叶热传导定律（求物体边界流入的热量）：
  • 物体在dt内流过dS的
  • 是在点(x,y,z)处的热传导系数
  • v是曲面dS的法线。
    是法线方向的方向导数
• 任取物体G的一微分小块，其闭曲面为S，包围区域为D
• u(x,y,z)是在点(x,y,z)的温度

1) 温度变化而吸收的热量

2) 物体边界流入的热量

由散度定理，可将上式化为：

3) 热源在区域D内产生的热量

热源强度F(x,y,z,t)

4）能量守恒定律得到热传导方程

因为t1、t2与区域D是任意的，且被积函数是连续函数，所以G内任意一点任意时刻均有

化简，即得到热传导方程一般形式

无热源：

一维：

二维：

Laplace方程 拉普拉斯方程

• Laplace 算子

• 三维Lalpace方程
  • 三维热传导方方程：经过相当长时间后，无热源物体内各点的温度随时间变化而发生的变化已不显著，近似用
    表示，这样，即可得到拉普拉斯方程：

• • 三维弦振动方程：经过相当长时间后，振动处于平衡状态，即
    ，也可推导出上式。