11-11
每年双 11 都是电商们的重头戏。
巨大又集中的交易流量不仅是对电商来说是挑战,对「支付能力」等基础服务更是如此。
偏偏在这样的重要节点,支付宝崩了。
双 11 当天上午,支付宝出现无法登录、付款不成功、转账失败等严重问题。
更要命的是,这突如其来的故障给了用户们地狱般的体验:银行卡重复扣款,但订单却显示交易关闭。
出故障的技术原因或许会千差万别,但带来的体验影响,真的很难有比这更糟糕的了。
作为一个支付软件,重复扣款,且还一直显示支付失败,涉及金额交易对账问题,对用户信心的打击是致命的:
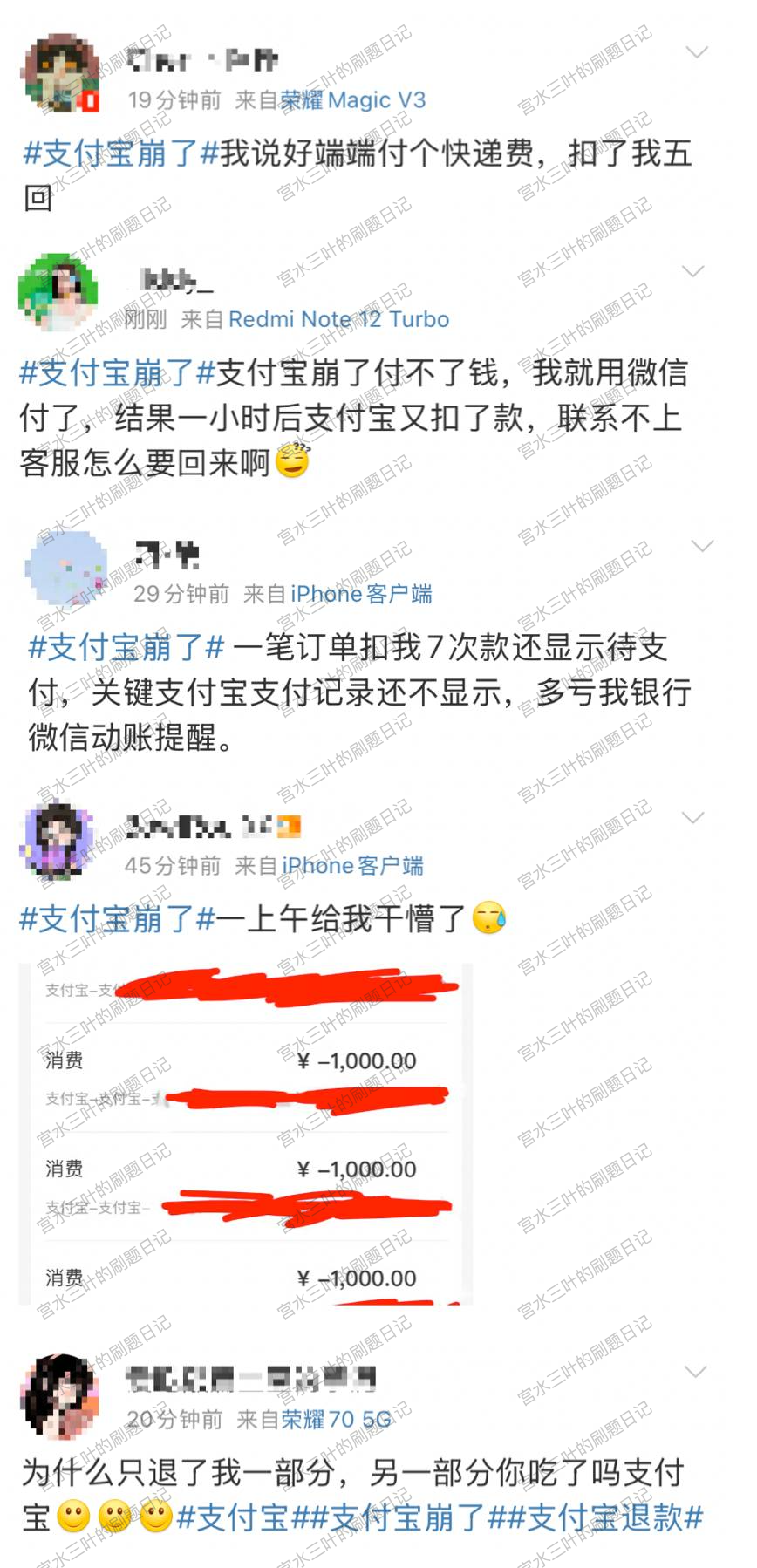
再后来,大概是上午 11 点半左右,支付宝官方微博,正式发了故障解除的通知:
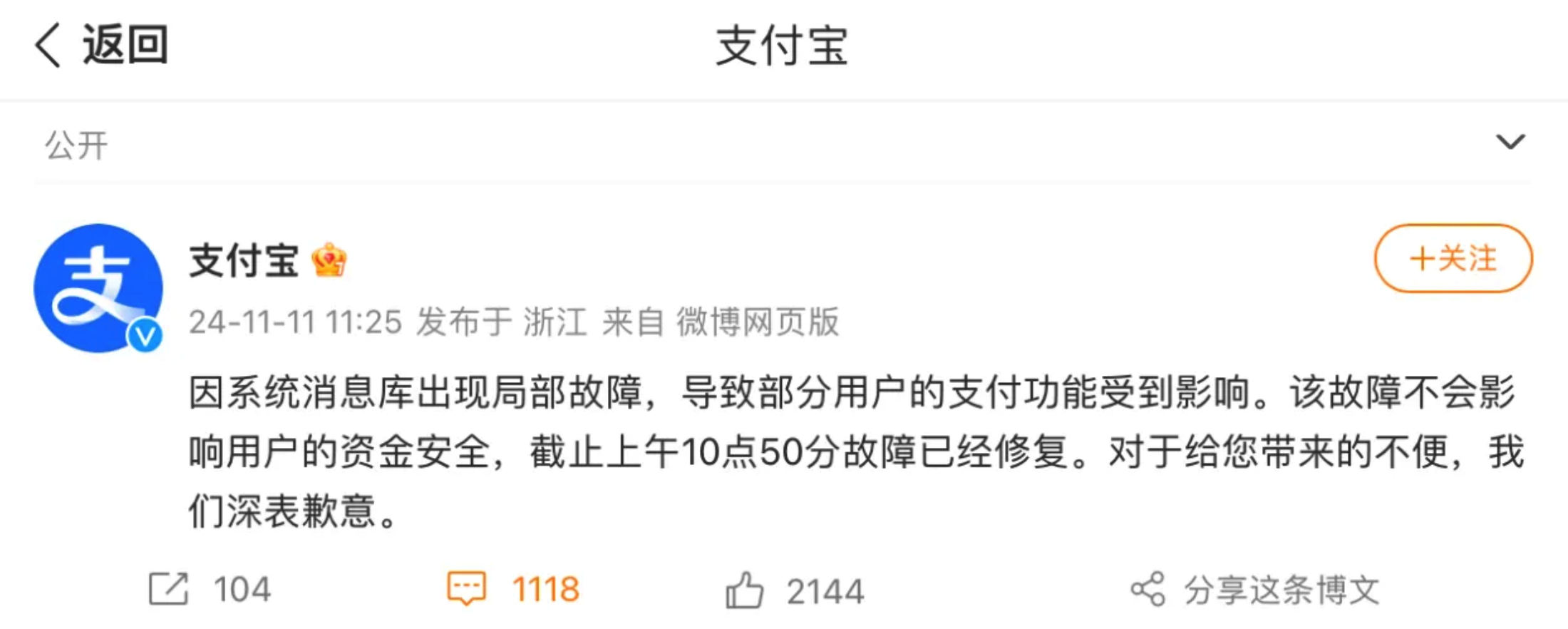
但凭心而论,切身经历过这次支付宝事故的用户,估计往后很难对支付宝没有别的看法。
...
另外,这次支付宝事故,还有一个很有意思的地方。
就是这次事故带来的泼天的流量,被微信支付接住了 🤣🤣🤣
因为一些政策上的原因,在今年早些时候,各个大厂之间决定打破某些存在多年的"壁垒",比如在淘宝使用微信支付,在微信查看淘宝商品等等。
于是这次支付宝故障,直接成就了「在双 11 当天,有大量淘宝订单,使用"微信支付"完成了交易」,你细品该成就的含金量。
要知道,双 11 可是一个由阿里"首创"的电商购物节。
支付宝却在这天当着全国网友的面,出了大糗,这谁能想到?
对此,你怎么看?
你今天是否有经历到该事故?平时是用「微信支付」比较多还是「支付宝」比较多?欢迎评论区交流。
...
回归主题。
来一道和「秋招」相关的算法题。
题目描述
平台:LeetCode
题号:363
给你一个 m x n 的矩阵 matrix 和一个整数
,找出并返回矩阵内部矩形区域的不超过
的最大数值和。
题目数据保证总会存在一个数值和不超过 的矩形区域。
示例 1:
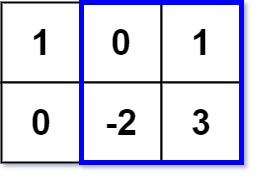
输入:matrix = [[1,0,1],[0,-2,3]], k = 2
输出:2
解释:蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2,且 2 是不超过 k 的最大数字(k = 2)。
示例 2:
输入:matrix = [[2,2,-1]], k = 3
输出:3
提示:
-
-
-
-
-
-
朴素二维前缀和
从题面来看显然是一道「二维前缀和」的题目,如果你还不了解「二维前缀和」,可以看看 (题解)304. 二维区域和检索 - 矩阵不可变。本题预处理前缀和的复杂度为 。
搜索所有子矩阵需要枚举「矩形左上角」和「矩形右下角」,复杂度是 。
因此,如果把本题当做二维前缀和模板题来做的话,整体复杂度是 。
数据范围是
,对应的计算量是
,理论上会超时,但当我们枚举「矩形左上角」
的时候,我们只需要搜索位于
的右下方的点
作为「矩形右下角」,所以其实我们是取不满
的,但仍然具有超时风险(2021/04/20 Java 测试可通过,C++ 使用 vector 会 TLE)。
Java 代码:
class Solution {
public int maxSumSubmatrix(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
int[][] sum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
int ans = Integer.MIN_VALUE;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
for (int p = i; p <= m; p++) {
for (int q = j; q <= n; q++) {
int cur = sum[p][q] - sum[i - 1][q] - sum[p][j - 1] + sum[i - 1][j - 1];
if (cur <= k) {
ans = Math.max(ans, cur);
}
}
}
}
}
return ans;
}
}
C++ 代码:
int sum[110][110];
class Solution {
public:
int maxSumSubmatrix(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
int ans = INT_MIN;
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
for(int p = i; p <= m; p++){
for(int q = j; q <= n; q++){
int cur = sum[p][q] - sum[i - 1][q] - sum[p][j - 1] + sum[i - 1][j - 1];
if(cur <= k){
ans = max(ans,cur);
}
}
}
}
}
return ans;
}
};
-
时间复杂度:预处理前缀和数组复杂度为 ,查找答案的复杂度为 。整体复杂度为 。 -
空间复杂度:
前缀和 & 二分(抽象一维)
我们来细想一下「朴素二维前缀和」解法是如何搜索答案(子矩阵):「通过枚举「左上角」&「右下角」来唯一确定某个矩阵」。
「换句话说是通过枚举 和 来唯一确定子矩阵的四条边,每个坐标点可以看作确定子矩阵的某条边。」
既然要确定的边有四条,我们可以如何降低复杂度呢?
简单的,我们先思考一下同样是枚举的 1. 两数之和 问题。
在 1. 两数之和 中可以暴力枚举两个数,也可以只枚举其中一个数,然后使用数据结构(哈希表)来加速找另一个数(这是一个通用的「降低枚举复杂度」思考方向)。
对应到本题,我们可以枚举其中三条边,然后使用数据结构来加速找第四条边。
当我们确定了三条边(红色)之后,形成的子矩阵就单纯取决于第四条边的位置(黄色):
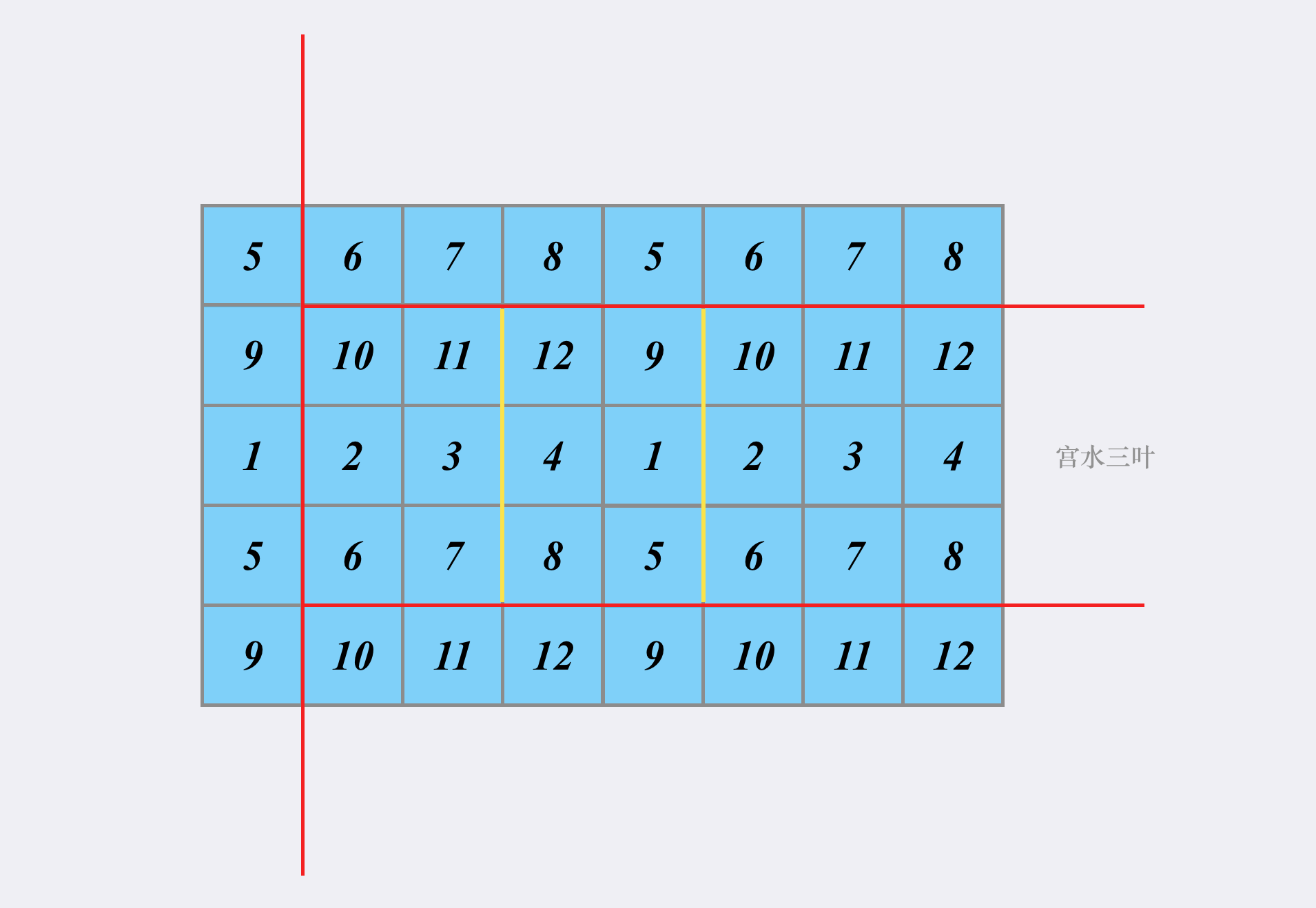
于是问题转化为「「如何快速求得第四条边(黄色)的位置在哪」」。
我们可以进一步将问题缩小,考虑矩阵只有一行(一维)的情况:
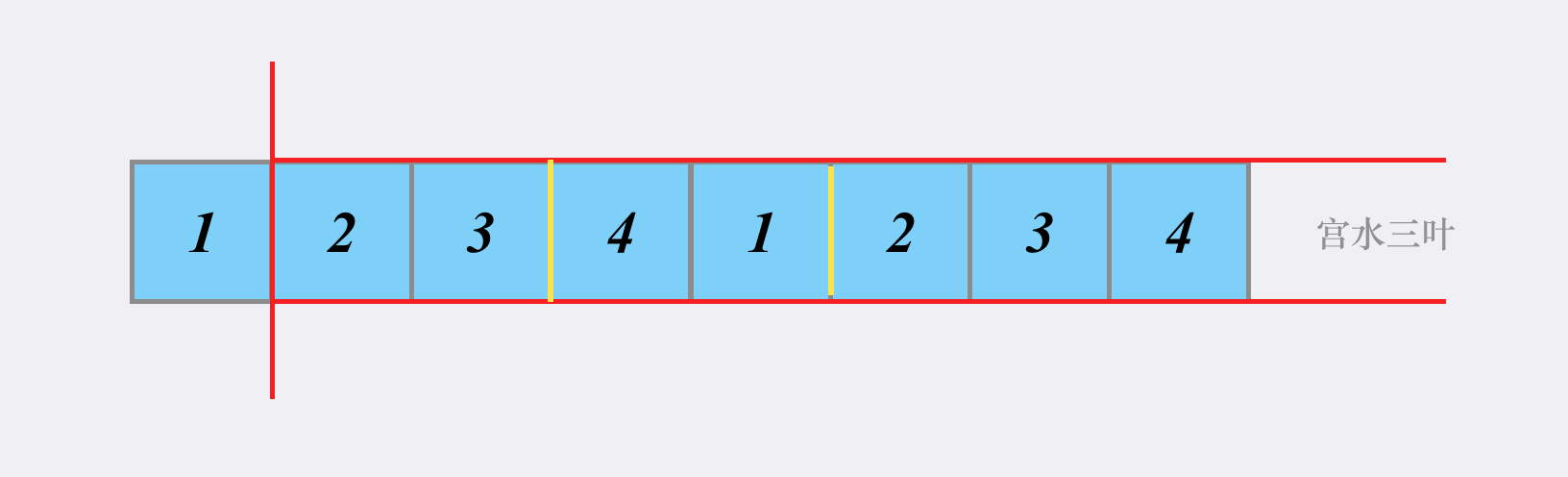
这时候问题进一步转化为「「在一维数组中,求解和不超过 K 的最大连续子数组之和」」。
对于这个一维问题,我们可以先预处理出「前缀和」,然后枚举子数组的左端点,然后通过「二分」来求解其右端点的位置。
假定我们已经求得一维数组的前缀和数组 sum,即可得下标范围
的和为:
经过变形后得:
我们有两种思路来最大化 :
-
确定(枚举)左端点位置 i,求得符合条件的最大右端点sum[j] -
确定(枚举)右端点位置 j,求得符合条件的最小左端点sum[i]
「对于没有负权值的一维数组,我们可以枚举左端点 i,同时利用前缀和的「单调递增」特性,通过「二分」找到符合
条件的最大值 sum[j],从而求解出答案。」
「但是如果是含有负权值的话,前缀和将会丢失「单调递增」的特性,我们也就无法使用枚举 i 并结合「二分」查找 j 的做法。」
「这时候需要将过程反过来处理:我们从左到右枚举 j,并使用「有序集合」结构维护遍历过的位置,找到符合
条件的最小值 sum[i],从而求解出答案。」
基于上述分析,解决这样的一维数组问题复杂度是 的。
将这样的思路应用到二维需要一点点抽象能力。
同时,将一维思路应用到本题(二维),复杂度要么是 要么是 。
我们先不考虑「最大化二分收益」问题,先假设我们是固定枚举「上下行」和「右边列」,这时候唯一能够确定一个子矩阵则是取决于「左边列」:
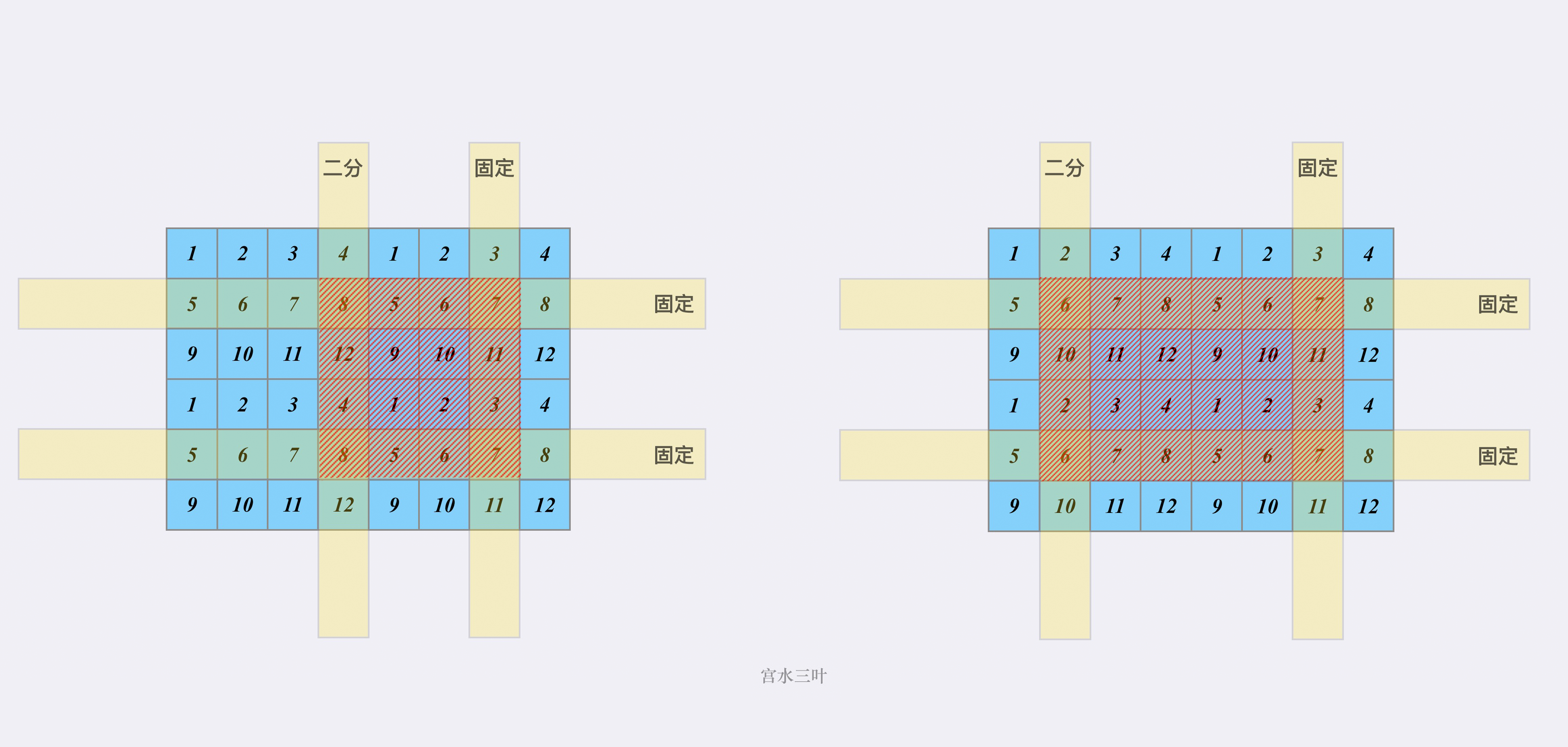
「重点是如何与「一维」问题进行关联:显然「目标子矩阵的和」等于「子矩阵的右边列 与 原矩阵的左边列 形成的子矩阵和」-「子矩阵左边列 与 原矩阵左边列 形成的子矩阵和」」
我们可以使用 area[r] 代表「「子矩阵的右边列 与 原矩阵的左边列 形成的子矩阵和」」,使用 area[l - 1] 代表「「子矩阵的左边列 与 原矩阵的左边列 形成的子矩阵和」」的话,则有:
这与我们「一维问题」完全一致,同时由「上下行」&「右边列」可以直接确定 area[r] 的大小,通过「有序集合」存储我们遍历 r 过程中的所有的 area[r] 从而实现「二分」查找符合
条件的 「最小」 的 area[l - 1]。
至此,我们通过预处理前缀和 + 容斥原理彻底将题目转化为「一维问题」进行来求解。
Java 代码:
class Solution {
public int maxSumSubmatrix(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
// 预处理前缀和
int[][] sum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
int ans = Integer.MIN_VALUE;
// 遍历子矩阵的上边界
for (int top = 1; top <= m; top++) {
// 遍历子矩阵的下边界
for (int bot = top; bot <= m; bot++) {
// 使用「有序集合」维护所有遍历到的右边界
TreeSet<Integer> ts = new TreeSet<>();
ts.add(0);
// 遍历子矩阵的右边界
for (int r = 1; r <= n; r++) {
// 通过前缀和计算 right
int right = sum[bot][r] - sum[top - 1][r];
// 通过二分找 left
Integer left = ts.ceiling(right - k);
if (left != null) {
int cur = right - left;
ans = Math.max(ans, cur);
}
// 将遍历过的 right 加到有序集合
ts.add(right);
}
}
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int maxSumSubmatrix(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
vector<vector<int>> sum(m + 1,vector<int>(n + 1,0));
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
int ans = INT_MIN;
for(int top = 1; top <= m; top++){
for(int bot = top; bot <= m; bot++){
set<int> st;
st.insert(0);
for(int r = 1; r <= n; r++){
int right = sum[bot][r] - sum[top - 1][r];
auto left = st.lower_bound(right - k);
if(left != st.end()){
int cur = right - *left;
ans = max(ans,cur);
}
st.insert(right);
}
}
}
return ans;
}
};
-
时间复杂度:枚举上下边界复杂度为 ;枚举右边界为 ,使用 TreeSet(基于红黑树)存储和查找左边界复杂度为 。整体复杂度为 -
空间复杂度:
最大化「二分」效益
上述解法中,我们先枚举的是「上下行」和「右边列」,然后通过 TreeSet 来「二分」出符合条件的「左边列」。
事实上,我们需要将「二分过程」应用到数值较大的行或者列之中,这样才能最大化我们查找的效率(同时也回答了本题的进阶部分)。
Java 代码:
class Solution {
public int maxSumSubmatrix(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
int[][] sum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
// 固定的是否为右边界
boolean isRight = n > m;
int ans = Integer.MIN_VALUE;
for (int i = 1; i <= (isRight ? m : n); i++) {
for (int j = i; j <= (isRight ? m : n); j++) {
TreeSet<Integer> ts = new TreeSet<>();
ts.add(0);
for (int fixed = 1; fixed <= (isRight ? n : m); fixed++) {
int a = isRight ? sum[j][fixed] - sum[i - 1][fixed] : sum[fixed][j] - sum[fixed][i - 1];
Integer b = ts.ceiling(a - k);
if (b != null) {
int cur = a - b;
ans = Math.max(ans, cur);
}
ts.add(a);
}
}
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int maxSumSubmatrix(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
vector<vector<int>> sum(m + 1,vector<int>(n + 1,0));
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + mat[i - 1][j - 1];
}
}
bool isRight = n > m;
int ans = INT_MIN;
for(int i = 1; i <= (isRight ? m : n); i++){
for(int j = i; j <= (isRight ? m : n); j++){
set<int> st;
st.insert(0);
for(int fixed = 1; fixed <= (isRight ? n : m); fixed++){
int a = isRight ? sum[j][fixed] - sum[i - 1][fixed] : sum[fixed][j] - sum[fixed][i - 1];
auto b = st.lower_bound(a - k);
if(b != st.end()){
int cur = a - *b;
ans = max(ans,cur);
}
st.insert(a);
}
}
}
return ans;
}
};
-
时间复杂度:预处理「每行」或「每列」的前缀和,复杂度为 ;枚举子矩阵的「上下行」或「左右行」,复杂度为 ;结合二维前缀和套用一维最大连续子数组解决方案,复杂度为 。整体复杂度为 -
空间复杂度:
空间优化
不难发现,我们在原矩阵搜索目标子矩阵的过程是严格的「从上到下」&「从左到右」的。
因此我们可以将计算前缀和的逻辑下放到搜索子矩阵的循环里去做,从而将 的空间复杂度下降到 。
Java 代码:
class Solution {
public int maxSumSubmatrix(int[][] mat, int k) {
int m = mat.length, n = mat[0].length;
boolean isRight = n > m;
int[] sum = isRight ? new int[n + 1] : new int[m + 1];
int ans = Integer.MIN_VALUE;
for (int i = 1; i <= (isRight ? m : n); i++) {
Arrays.fill(sum, 0);
for (int j = i; j <= (isRight ? m : n); j++) {
TreeSet<Integer> ts = new TreeSet<>();
ts.add(0);
int a = 0;
for (int fixed = 1; fixed <= (isRight ? n : m); fixed++) {
sum[fixed] += isRight ? mat[j - 1][fixed - 1] : mat[fixed - 1][j - 1] ;
a += sum[fixed];
Integer b = ts.ceiling(a - k);
if (b != null) {
int cur = a - b;
ans = Math.max(ans, cur);
}
ts.add(a);
}
}
}
return ans;
}
}
C++ 代码:
class Solution {
public:
int maxSumSubmatrix(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
bool isRight = n > m;
vector<int> sum((isRight ? n + 1 : m + 1), 0);
int ans = INT_MIN;
for(int i = 1; i <= (isRight ? m : n); i++){
fill(sum.begin(),sum.end(),0);
for(int j = i; j <= (isRight ? m : n); j++){
set<int> st;
st.insert(0);
int a = 0;
for(int fixed = 1; fixed <= (isRight ? n : m); fixed++){
sum[fixed] += isRight ? mat[j - 1][fixed - 1] : mat[fixed - 1][j - 1];
a += sum[fixed];
auto b = st.lower_bound(a - k);
if(b != st.end()){
int cur = a - *b;
ans = max(ans,cur);
}
st.insert(a);
}
}
}
return ans;
}
};
-
时间复杂度:预处理「每行」或「每列」的前缀和,复杂度为 ;枚举子矩阵的「上下行」或「左右行」,复杂度为 ;结合二维前缀和套用一维最大连续子数组解决方案,复杂度为 。整体复杂度为 -
空间复杂度:
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉























 1710
1710

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








