一阶微分方程的物理意义_（广义）全微分方程

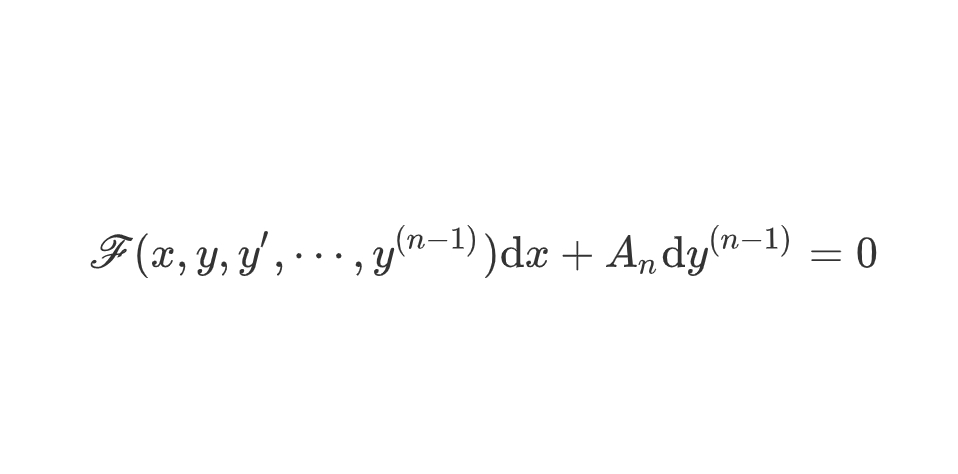
本篇来源于《微分方程（解法和解）》^[1]（E·卡姆克）中15.1全微分方程一节。当然，原文中没有“广义”一词，因此在标题上加了一个括号。

原文极其简洁。甚至几行便可引用完这一节的全文：

全微分方程。微分方程

称为全微分方程，如果存在着函数

，使得

对于变量

成为恒等。因为某一

次可微函数

，当且仅当

时，是方程

的解，所以全微分方程总可以化为较低阶的方程。

如果

具有直到

阶为止的连续偏导数，并且如果要求

具有直到二阶为止的连续偏导数，则使得微分方程

是全微分方程的条件如下：假设

这时，函数

应当与

无关，而

应当等于

，特别是，

只能线性地包含在

中。

这是老工具书类型教材一贯的表述语言…但是去稍微查找一下有关类似全微分方程的文献，却没能找到这样的。能翻到的都是高阶变系数线性的“全微分方程”，有点失望。

于是本篇即为对以上内容的解读，以及尝试按照二元全微分方程的路线构建出部分多元（其实是三元）全微分方程的分项组合法。不能保证完全正确，推导证明过程很可能是有很大漏洞的，不过方法应该是“可用”的/躺。

当尝试使用这些方法去解一些具体的问题（二阶微分方程）的时候，骤然发现这似乎并没有什么用，因为有用的高阶方程都已经命上名了…而且遇见这样一个残破的轮子肯定也是前人（dalao）尝试造过然后摇摇头说造不了的。于是本文也仅供君一乐/叹气。

---

正文

引子

首先回顾一下二元的全微分方程。此时的全微分方程有一个更广泛的名字：恰当微分方程。其形式为：

这样的形式可认为是由

认为

二者“平权”，乘上

而来。由于

可视为全微分的形式（如果有

）。因此对于二元的恰当微分方程总以此形式进行处理。

但是实际上称一个方程是“一阶微分方程”，依旧是以

的形式判定。可见，

形式的全微分方程是不易按照阶数去推广的：一个二阶的全微分方程按

书写是怎样的形式？一阶微分方程可以有

的书写表达，但二阶却万

不可出现

。

而对于

，很简单的就可以进行推广。一个

稍有限制的

阶微分方程总

认为可有形式：

其中

为函数

，而不能出现

本身（实际上这里是全微分方程的第一个判定了）。其中，我们可以将

（包括首项

）这样的项命名为“旗标项”。后面可以看见，旗标项其实是理想化的产物。

当此微分方程其满足一定形式的时候，是全微分方程。先考察方程

。显然地，对于某一函数

，若仅认为其关于

为自变量，则对

求导：

若系数对应相等：