一阶微分方程的物理意义_常微分方程学习笔记(9)

经过长时间的消化，我来尝试更一下微分方程的笔记好了。这一章大概是对一些比较前沿的领域的入门介绍，概念非常多，许多定理也不给证明，挺难受的。为了叙述的严谨性，有时候会略微增加一点书上没有的东西。

看这一章时最好调动自己的直觉，有一些东西严格定义很晦涩，却是可以直观想象的。笔记比较长，要看的话建议分两段。

封面是番剧『宇宙よりも遠い場所』的图，可以了解一下。(好像变成了番剧推荐2333)

第八章 定性理论与分支理论初步

再安利一下，下面视频的部分内容对于建立这一章内容的感性认识比较有帮助。

【维度】数学漫步第一季（熟肉）[2008]_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili​www.bilibili.com

维度：数学漫步2—混沌_哔哩哔哩 (゜-゜)つロ 干杯~-bilibili​www.bilibili.com

在最开始我们要先引入一些基本概念，在后面十分常用。这就是动力系统，相空间和轨线的概念。

8.1 动力系统，相空间和轨线

我们从物理开始。假设在

维空间里有一个质点，它在时刻

的坐标为

，运动速度为

。则可以得到方程

这是一个自治的微分方程。假设它满足解的存在唯一性条件，则它在初值条件

下有唯一解

。这个解描述了质点在时刻

经过点

的运动。我们称

取值的空间(

)为

相空间，称

取值的空间(

)为

增广相空间。可以在增广相空间中画出线素场(点

处短线段与向量

共线)，上述方程的解在增广相空间中确定了一条曲线，处处与线素场相切。

在动力系统理论中我们更习惯使用向量场(物理学会叫它速度场)的提法，也就是说在相空间的每一个点

处有一个向量

与之对应。如果考虑相空间，上述解在相空间内描绘了一条曲线，这曲线处处与向量场相切，我们称它为

轨线。轨线在上面的物理描述中就是质点运动的轨迹，而积分曲线是所谓的「时空线」。通常规定轨线的方向是

增大的方向。

轨线与方程的积分曲线有简单的关系：轨线是积分曲线在相空间上的投影，前者是

维空间中的曲线，后者是

维空间中的曲线。大家可以利用

的情形来想象。

所谓相图是指轨线族的结构图。定性理论正是要研究微分方程相图的拓扑结构，因此又被称为微分方程的几何理论。

下面引入奇点和闭轨的概念，这是定性理论研究的两大重要模型。

如果

是速度场

的零点，即

，则方程有一个定常解

。这个点叫做

平衡点，意味着质点的静止状态。这个解在相空间里是一个点

，在增广相空间里是一条垂直于相空间的直线。此时点

就是一条退化的轨线。由于后面我们会在这个点附近看到许多奇怪的现象，又称它为

奇点。

如果对于某个

，解

对

是非定常周期的，则它在相空间中的轨线是闭曲线，称为

闭轨。质点在闭轨上不断做着周而复始的运动。

对奇点与闭轨的分析是两大重点问题，下面看一个例子。

质点在

平面上运动，其速度的两个分量满足

。分析这个质点可能的轨线族。

用极坐标代换，设

。代入计算得

。

解得

。令

，则得

。设单位圆周

，则

在

内部(外部)等价于

。于是

(1)若

，则轨线是唯一的奇点

。

(2)若

在

上，则轨线就是逆时针方向的圆周

。这是唯一的闭轨。

(3)若

在

内且不同于奇点，则轨线在圆内，且当

时逆时针盘旋趋于奇点，

时顺时针盘旋趋于圆周

。

(4)若

在

外，则轨线在圆外，且当

时逆时针盘旋趋于远处，

时顺时针盘旋趋于圆周

。

大家可以画一画相空间以及增广相空间中的情况以方便理解。

两种轨线的形状

上述的微分方程

称为一个

动力系统。动力系统有下面的性质：

1.积分曲线平移不变性

把积分曲线沿

轴平移任意长度，所得依然是积分曲线。这由自治性就可以得知。

2.过相空间每一点轨线的存在唯一性

存在性由解的存在性保证，至于唯一性，假设有两条轨线都过一点，考虑它们对应的积分曲线，这两条曲线可以通过平移使得它们交于一点(性质1)，但是由解的唯一性，这两条积分曲线必然是同一条，从而投影后的轨线也是同一条。

这两条性质还说明，每条轨线可以对应于一族积分曲线，这些积分曲线互为平移。由性质1，对于任意一个解

,函数

也是解，且满足相同的初值条件。从而由唯一性，

。从而在解族中只需要考虑初始时刻

的解。下面记

。

3.群的性质

在运动中，质点的轨迹如果确定，那么从固定起点开始运动

秒与先运动

秒再运动

秒是一样的。用式子写出来就是：

。

下面给出数学的证明：由性质1知

都是方程的解，而且

与

在

的初值都等于

。由唯一性定理知它们相等。令

就得到要证的式子。

不妨假设对于任意

，上述解

都在

存在。这是因为考虑另一个方程

，利用解的存在区间相关定理可以证明这个方程的解在

存在，且与

有相同的轨线。

现在我们发现，对于一个固定的

，上述解把一个向量

变成另一个向量

。记这个变换为

，则集合

满足下面的性质：

(1)

是恒等变换；

(2)

;

(3)

对

在

是连续函数。

这说明集合

在映射复合运算

下构成一个

加法群。

是单位元，而

是

的逆元。这样的具有上面三个性质的单参数连续变换群叫做

抽象动力系统( 拓扑动力系统)。如果

可微，这又可以叫做

微分动力系统。

最后说一下非自治微分方程的情况。对于微分方程

，

，我们令

，则

，就是一个

维的自治的动力系统了。

8.2 解的稳定性

之前有研究过微分方程的解对初值的连续依赖性，那里的方法只适合自变量在有限闭区间取值的情形。而在自变量扩展到无穷区间时，这一连续性将被破坏，产生所谓混沌现象。Lyapunov(李雅普诺夫)研究了这一类问题，发展了Lyapunov稳定性的概念。其中三个核心概念是渐进稳定，稳定与不稳定。先通过例子直观认知它们。在上一小节的例子中，初值点只要在圆周

内部，其轨线总是随着

的增大趋于平衡点

。这时我们称平衡点是渐进稳定的。再考虑单摆的振动方程

，即

，这是一个二维动力系统。这玩意的相图大概是这样：

不会用软件画相图。。。谁来教教我

上图中点

具有如下特点，只要初值点足够靠近它，对应的轨线就会停留在

的充分小的邻域内。而

附近的轨线无论多么靠近，最终都会远离这个点。二者都是平衡点，但是前者是稳定的，后者是不稳定的。

下面正式引入这些稳定性的概念：

考虑方程

，其中函数

在

与

连续，且对

满足Lipschitz条件。假设方程有一个解

在

有定义。

如果对于任意的

都存在

使得只要

, 就有

在

有定义且

，其中

是方程满足初值

的解。则称解

是(Lyapunov意义下)

稳定的。

如果解

是稳定的，且存在

使得只要

就有

，则称解

是

渐进稳定的。如果解

不是稳定的，称它为

不稳定的。大家可以在脑子里把直观认识和严格定义对应起来，这样更好用。

如果对于区域

有：对于

，

,且也有

,则称

为解

的

渐进稳定域(或 吸引域)。如果吸引域是全空间，就称解

是

全局渐进稳定的。

如果把

的趋向变成

，还可以定义负向的稳定性概念，但是我们这里只考虑正向稳定性。

为了方便讨论，只介绍零解的稳定性判断，其中

。因为可以用代换

来转化。下面介绍线性近似法与Lyapunov第二方法

^[1]。

1.线性近似法

许多微积分的教材定义微分的时候是通过定义线性主要部分来做的。同样，这里我们在方程

中令

，其中

为矩阵函数，对

连续；

在区域

连续，对

满足Lipschitz条件，且满足

，以及

对

一致成立。

我们推测，原来的方程的稳定性与其线性化方程

的稳定性之间是有联系的。只要「扰动」

足够小，就不会影响稳定性。这里我们暂时只考虑

为常数矩阵的情形。先来叙述关于线性化方程的定理，证明不太难。

定理 线性化方程

的零解稳定性判定：

(1)零解是渐进稳定的，等价于矩阵

的所有特征值有负的实部；

(2)零解是稳定的，等价于矩阵

的所有特征值有非正的实部，且那些实部为零的特征值对应的Jordan块都是一阶的；

(3)除此之外零解都是不稳定的。

我们知道，上述方程的基本解矩阵是

，而满足

的解是

。只要估计矩阵指数。设

，

是Jordan标准形。则

。把

中的每一项都计算出来(在第六章已经计算过)，然后利用指数函数的性质就可以得到结论了。

下面是一般情况的定理，可以看到有一定联系。

定理 如果矩阵

的所有特征值有负的实部，则方程

的零解是渐进稳定的；如果矩阵

有特征值有正的实部，则方程的零解是不稳定的。

这个定理证明需要推广的Gronwall不等式。书上没有写证明，我自己想了一下证出来了，说一下思路。与之前做过许多遍的一样，使用函数逼近法。

推广的Gronwall不等式可以这样叙述：设连续函数

满足不等式

，其中

为常数，则有估计式

，其中

。我们只说前一半命题。

先证明原方程等价于积分方程

。然后，构造函数序列

满足

，且

。

这时候序列

就符合Gronwall不等式的条件了(注意，那些矩阵指数其实都很小)。通过这个证明函数序列

一致收敛于

，且

在

时趋于零，就可以证明命题。

2.Lyapunov第二方法

这个方法充分说明一件事：Lyapunov是一个天才。这个方法是怎么想到的，可能也只有问Lyapunov了。不过学物理的人有时会把这种方法看成构造一种「能量」，大家可以体会一下。

先考虑简单的情况，微分方程组

。对于任意具有连续一阶偏导数的二元函数

，我们代入上面微分方程的解

，并对

求导可得

得到的结果如果不代入

其实与

无关。这个函数叫做

关于微分方程的全导数，它的几何意义是函数

沿着微分方程的轨线的方向导数。对于一般的

元函数，以及自治微分方程

，

关于微分方程的全导数可以表示为

，其中

是Nabla算子。不混淆的情况下有时也可以简称为

全导数。

为了说明这个概念的应用，先看之前关注过的例子：

。

我们构造函数

，这个函数满足两个条件。

(1)函数是正定的，即

，等号成立当且仅当

。(类似可以说明什么是

半正定函数， 负定函数， 半负定函数)

(2)当

时，

的全导数为

。

注意，对于任意的

，

在相平面上的图像是环绕原点的闭曲线

。对于不同的

，

互不相交，且随着

收缩到原点。轨线随着

的增大由外而内依次穿过所有的

，最后趋向于原点。所以可以推测，零解是渐进稳定的。数学证明如下：假设

，其中

，则全导数为

。由此可推出

，矛盾。故

，由连续性可知

。从而零解是渐进稳定的。

对于一般的微分方程

，有下面的定理。

定理 (Lyapunov稳定性判据)方程的零解是渐进稳定的，如果存在上面所述的函数

(通常称为

Lyapunov函数)，在区域

有定义，且满足

是正定的，其全导数是负定的；方程的零解是稳定的，如果存在上面所述的函数

，满足

是正定的，其全导数是半负定的；方程的零解是不稳定的，如果存在上面所述的函数

，满足

是正定的，其全导数是正定的。(关于最后一个命题有更强的结论：零解是负向渐进稳定的)

懒得敲证明......请见问题：

如何用李雅普诺夫第二法分析非线性系统在每个平衡点处的稳定性？​www.zhihu.com

用人话说证明思路大概就是，用连续性说明稳定性，证明极限

并配合连续性以说明渐进稳定性。

这个方法很厉害，但是怎么构造Lyapuonv函数是玄学。下面说一些例子。

(1)常系数线性微分方程组

。

令

，

是待定实对称矩阵。则其全导数为

。这时候问题就变为找一个正定矩阵

使得矩阵

为负定/半负定/正定。这时候可以预先找一个负定/半负定/正定矩阵

，问题就变成矩阵方程

。

(2)

。(

在原点附近可微)

令

。为什么这样构造？

微分方程的结构中可以发现

，这样就很明显了。方程的稳定性与

的性质有关。

(3)

，其中

。

方程可以变为

。我们考虑一个质点，它在位移为

的时候速度为

，加速度为

。这个加速度可以视为一个回复力的作用。假设质点质量为

，那么系统的能量为

。之前说过Lyapunov函数可以看成一种能量，我们验证一下在这个例子上是否好用。首先由条件可以证得

是正定的。其次，

的全导数为

，计算得为零，是半负定函数。所以零解是稳定的。请大家证明零解不是渐进稳定的。

Lyapunov函数的构造问题相当困难，这里只举了一些最简单的例子，更多的构造技巧请参见这里。

8.3 平面上的动力系统，奇点与极限环

这一节只研究平面上的动力系统：

。看起来似乎简单一些，因为有Jordan曲线定理的约束；然而这却是更多玄学的开始。

我们考虑把上面两式相除，得到

。这个方程的奇异点(使得右边函数没有意义的点)与动力系统的奇点是一样的。这个方程的一条积分曲线如果不包含奇点，那么就是动力系统的一条轨线；如果包含奇点，那么每一个被奇点分割出来的连通分支都是动力系统的一条轨线。相空间里不是奇点的点叫做

常点。在第五章证明过，系统在常点附近的轨线族拓扑同胚于平行直线族。所以，奇点将会是轨线族拓扑结构分析的一大重点。除此之外，闭轨因为是封闭的，也需要重点关注。

1.奇点

下面考虑这样的线性系统：

，其中

为常数矩阵，系统以

为奇点。如果矩阵

没有零作为特征值，则称

为

高阶奇点，否则称为 初等奇点。这里先讨论初等奇点，后面的节会有高阶奇点的例子。

设矩阵

满足

为Jordan标准形。做线性变换

，则

。从而，可以视作

已经是Jordan型矩阵。由于特征值可能是共轭复数，故还可以再对这种情况下的矩阵做变换，成为以下三种可能情况：

其中

。下面一一地讨论。

(1)第一种情况(两个非零实特征值)

这时方程是变量分离的，可以直接求解得到两个解：

与

。(第二个解就是

)

a.如果

，即有一个二重特征值，他有两个一阶Jordan块。如果

，那么所有的轨线在

增大时都趋于奇点

，从而奇点是渐进稳定的。如果

，那么所有的轨线在

增大时都趋于无穷远处，从而奇点是渐进稳定的。画成图就是

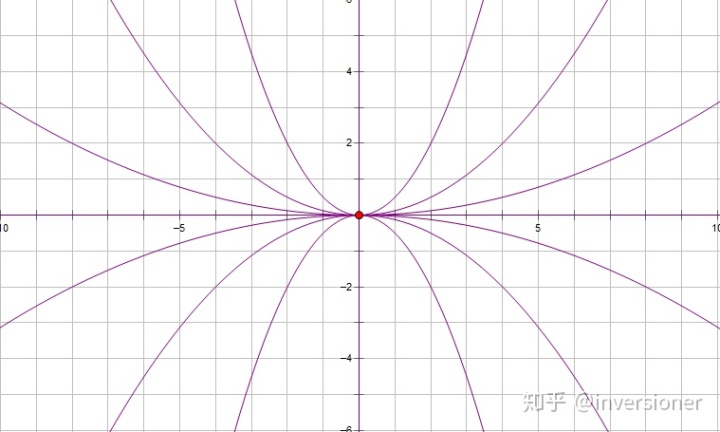
星形结点

这样的奇点我们称为星形结点(临界结点)。

b.如果

且

，即有两个同号相异特征值，则这些曲线都形似抛物线，当

时它们与

轴相切，当

时它们与

轴相切。每一条曲线都被奇点

分割为系统的两条轨线，且

时奇点是渐进稳定的，

时奇点是不稳定的。画成图就是

两向结点(1)

两向结点(2)

这样的奇点叫两向结点，或者简称结点。试想一下这个「两向」的涵义。

c.如果

且

，即有两个异号特征值，这时曲线族是

，

以及一系列形似双曲线的曲线，它们以前述两条直线为渐近线。此时显然奇点

是不稳定的，轨线从无穷远处接近奇点，然后又远离它。画成图就是

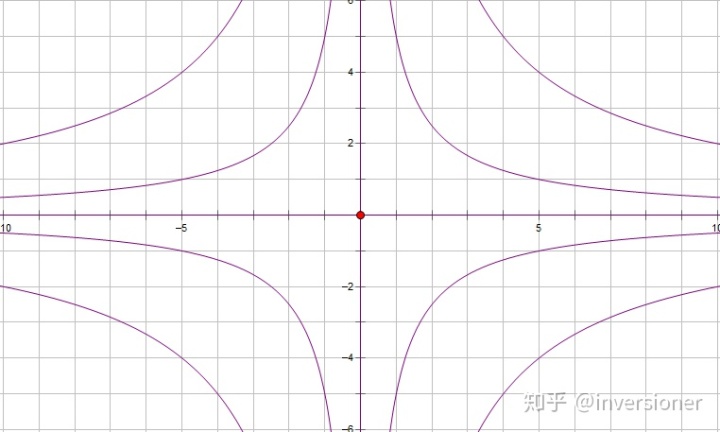
鞍点

这样的奇点叫做鞍点。

(2)第二种情况(一个非零二重特征值，对应二阶Jordan块)

此时方程的解为

与

。

(也就是

)

此时每条曲线都在

与

轴相切。若

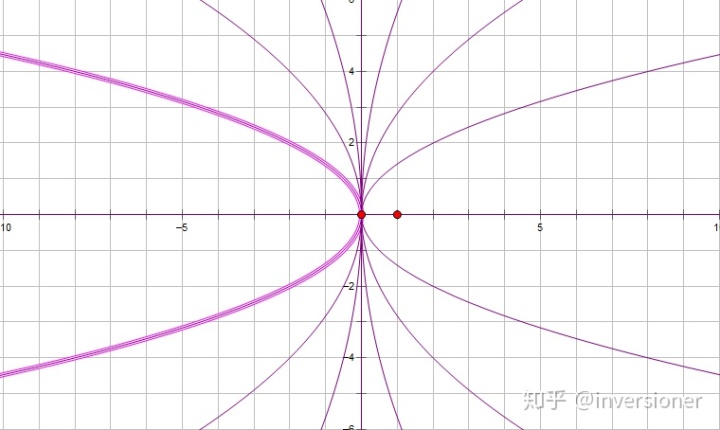
，则奇点是渐进稳定的，所有轨线从无穷远处趋近于奇点；否则是不稳定的，所有轨线从奇点趋于无穷远。画成图就是

单向结点

这种奇点叫做单向结点(退化结点)。

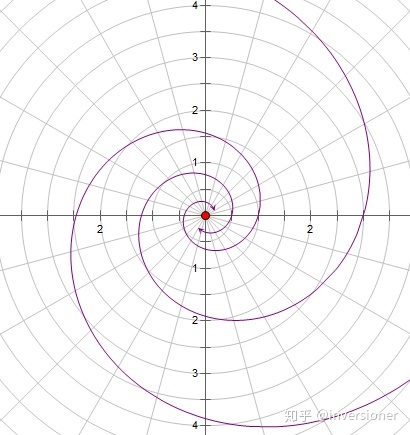
(3)第三种情况(两个共轭复特征值)

此时应用极坐标代换

，则系统变为

。解得通解为

。这是对数螺线。

的符号决定轨线的盘旋方向，而

的符号决定奇点的类型：

时轨线随着

的增大趋于奇点

，所以奇点是渐进稳定的，叫做

稳定焦点；

时轨线是同心圆族，这时奇点是稳定的但不是渐进稳定的，叫做

中心点；

时轨线随着

的增大从奇点趋于无穷远处，所以奇点是负向渐进稳定的，叫做

不稳定焦点。画成图就是

焦点

中心点

总结一下，初等奇点有六种类型：星形结点，两向结点，单向结点，鞍点，焦点，中心点。

以上讨论是在

已经是Jordan标准形的情况下做的，在线性变换

后这些特征依然不变，只是受到了一定的旋转和伸缩，

特殊方向(射线轨线)发生变化。注意到

的特征方程是

，我们有下面的定理。

定理 设系统有初等奇点

。记

。

则：(1)若

，则

为鞍点；(2)若

，则

为两向结点；(3)若

，则

为单向结点或者星形结点；(4)若

，则

为焦点；(5)若

，则

为中心点。另外，若

，则

是稳定的；若

则是不稳定的。

大家可以在

平面上标注这些不同的区域。

下面转向非线性系统的奇点类型问题。线性系统的特殊方向就是射线的轨线，而对于非线性系统，其特殊方向可以定义为(极坐标系的)一条射线

，满足存在点列

，当

时

，且

处的向量场与坐标向量的夹角正切趋于零。如果非线性系统

(

是

的高于一次的项)与对应的线性系统

有一样的特殊方向，且沿着这些特殊方向进入奇点的轨线(即随着

趋于奇点且与特殊方向相切)条数(包括

条)相同，则称它们在奇点附近有相同的

定性结构。此时对应的奇点可以与线性系统相同命名。

关于非线性系统的奇点有下面的定理。

定理 记

。给出下面三个条件：a.

；b.

；c.

在原点的某一邻域内对

可微。则：

(1)若

是对应线性系统的焦点，且成立条件a，则

是原系统的焦点且稳定性相同；

(2)若

是对应线性系统的鞍点(两向结点)，且成立条件a和c，则

是原系统的鞍点(两向结点)且稳定性相同；

(3)若

是对应线性系统的单向结点，且成立条件b，则

是原系统的单向结点且稳定性相同；

(4)若

是对应线性系统的星形结点，且成立条件b和c，则

是原系统的星形结点且稳定性相同。

定理书上不给证明，我也不会证(摊手)。更多信息在《微分方程定性理论》里会提到。

一种比保持定性结构更弱的要求是保持拓扑结构。

为此，记

为所有动力系统

的集合，其中

都可微。在

中两个系统的「距离」可以定义为式子

如果两个系统的距离总是小于

，称它们为

-邻近系统。

在

中两个系统

轨道拓扑等价是指存在拓扑同胚把一个系统的轨线族变为另一个系统的轨线族且保持定向。如果对于某一个系统，存在

使得它的任何

-邻近系统都与它轨道拓扑等价，则称该系统是

结构稳定的。关于非线性系统的结构稳定性有下面的结论。

Hartman-Grobman定理 如果上述非线性系统

有奇点

且线性部分矩阵的特征值实部均不为零(此时称奇点为

双曲奇点)，则系统在奇点附近是结构稳定的，且轨道拓扑等价于它对应的线性系统。

上述定理还可以推广到

中。非双曲奇点有两种，一种是高阶奇点；另一种是线性部分矩阵的特征值是纯虚数的情况，这时线性系统的奇点是中心点，但是加上高阶项以后可能变成焦点。

另外，只要稳定性相同，容易证明各类(初等)结点与焦点均彼此轨道拓扑等价。把稳定的结点和焦点叫做渊，不稳定的结点和焦点叫做源。(顺便说一句，我觉得这两个名字取得特别好)

2.极限环

如果动力系统

在闭轨

的某个环形邻域内不再有其他的闭轨，即孤立闭轨，则称这个闭轨

为

极限环。可以证明，存在极限环的一个环形邻域，使得经过这个邻域的轨线都会正向(

)或负向(

)盘旋趋于极限环

。(直观上很好理解，注意到轨线不会相交，画一画就知道)这也是极限环一词的来历。极限环有三种：如果内外侧的附近轨线都正向趋于极限环，则称其为

稳定极限环；如果都负向趋于极限环，则称其为 不稳定极限环；其他的都称为 半稳定极限环。注意这种稳定性与Lyapunov稳定性的区别。

极限环只会出现在复杂的非线性系统中。

下面介绍关于判断极限环存在性的方法。我们有下面的著名定理(大定理就别想着看到证明了)：

Poincaré-Bendixson环域定理 设

是两条简单闭曲线

围成的环域，且在闭区域

中动力系统没有奇点，从

或

出发的轨线不能离开区域

(或者不能进入区域

)如果

均不是闭轨，则动力系统在

中一定存在一条闭轨

，这条闭轨在区域

中不能连续缩为一点。

如果

的内部包含

，则称

是

外境界线，

是

内境界线。

这个定理的物理图景很明显：如果流体从环域

的边界流入，且

内没有渊或源，那么流体在

内有环流。可以证明，如果动力系统的向量场是解析函数，则这条闭轨一定是极限环。从而，许多现实中的问题都可以根据这个定理来判断。

例子：(van der Pol方程)证明系统

有极限环。

不妨取

。(其他情况类似)等价的动力系统为

。(把

以外的项移到另一边后对

积分，并令

)要作出环域并不容易。

先作内境界线。令Lyapunov函数

。(活 学 活 用)则

是正定的，且其全导数为

。等号成立当且仅当

。从而对于足够小的正数

，从

上出发的曲线一定会走向

外部。

下面用所谓Liénard作图法来确定外境界线。对于系统

，可以确定任意一点

处向量场的方向。过点

作

轴的平行线与曲线

相交于点

，过点

作

轴的平行线与

轴交于点

。过

作直线与

垂直，则点

的向量场与这条直线共线。

Liénard作图法

注意到曲线

的极小值在点

取到，令

充分大，以

为圆心，分别以

与

为半径作圆弧

，前者与

轴正半轴交于

，与直线

交于

；后者与

轴负半轴交于

，与直线

交于

。把曲线

关于原点做对称得到曲线

，从而得到闭曲线

。记为

。由Liénard作图法可知，在曲线

的圆弧部分，经过曲线的轨线都指向内部；在直线部分，因为

充分大时

，故直线段

处于曲线

的下方，即这条线段上

。故经过的轨线也指向内部。直线段

的情况类似。

所以

围成一个定理所述的环域，由Poincaré-Bendixson环域定理知道，这个系统在环域内一定有闭轨，而这个闭轨是极限环。

还可以证明这是唯一的极限环，但这十分困难。

Hilbert的二十三个数学难题中有一个就是关于极限环的。记

是二元

次多项式，那么对于给定的

，动力系统

的极限环最多个数

是多少？这个问题的难度有多高，一句话就可以说明：至今仍不知道

是不是有限数。

另外还有判断极限环不存在的定理，这定理比Poincaré-Bendixson环域定理要好用多了。就是下面的(原来在习题中)

Bendixson准则 函数

在单连通区域

内连续可微，且满足散度

。则系统

在

内不存在闭轨。

用反证法，假设有一条闭轨

。由Green公式：

其中

是

的内部。计算左边的式子，设闭轨

为

。则

最后一个等号是因为满足微分方程。从而

，由积分中值定理知存在点

使得

。这与条件矛盾。

最后介绍后继函数法，这是研究极限环的一大工具。设

是动力系统的闭轨，取

上一点

并作闭轨的法线

，

在内部。在法线上取一点

。由微分方程的解对初值的连续依赖性，只要

足够小，过点

的轨线一定会再次法线相交。设正向首次相交点为

，它被称为

的

后继点。把

映射到

的映射叫做

Poincaré映射(再次膜拜巨佬Jules Henri Poincaré)。

显然，Poincaré映射的不动点对应闭轨。

我们在这条法线上引入坐标：

为原点，外法线为正方向。设

的坐标是

，

的坐标是

，这个函数

叫做

后继函数。记

，通过

充分小时

的符号可以判断极限环的稳定性。

我们知道点

对应着

。设使得

的最大的

是

，则由Taylor公式得

。从而

为偶数时，

是半稳定极限环；

为奇数且

时为稳定极限环，

为奇数且

时为不稳定极限环。

如果

，称极限环为

单重极限环；

时称为

重极限环。我们有下面的定理：

定理 单重极限环一定是结构稳定的。也就是说，存在

和极限环

的环形邻域

，使得原系统的任何

-邻近系统都在

的内部有唯一闭轨，且与

的稳定性相同。

8.4 结构稳定与分支现象

这一节就算是很前沿的研究内容了，但是介绍得十分简略。大概思路是，先介绍了一个大范围的结构稳定性定理，然后对各种不符合定理的情形进行了分析，引出了近现代微分方程最有活力的研究课题之一：分支现象。

这一节也可以看成前面所学的一些综合应用，除了开始的定理之外都可以当成一些具体习题。最后一小节「奇异向量场的普适开折」是不会说的，因为我也看不明白。

先做一些假设。用

表示所有平面动力系统

的集合，其中

都在圆盘

内有定义且连续可微，而且向量场不与

相切。下面的定理给出了动力系统是结构稳定的充要条件，这是一个很彻底的结果。

定理 (Andronov,Pantriagen)在

中系统是结构稳定的充要条件为：

(1)它只有有限个奇点，且这些奇点都是双曲奇点；

(2)它只有有限条闭轨，且每条都是单重极限环；

(3)它没有从鞍点到鞍点的轨线。

我们之前都接触过(1)(2)的有关问题，但是没有接触过(3)。这里做一点说明。

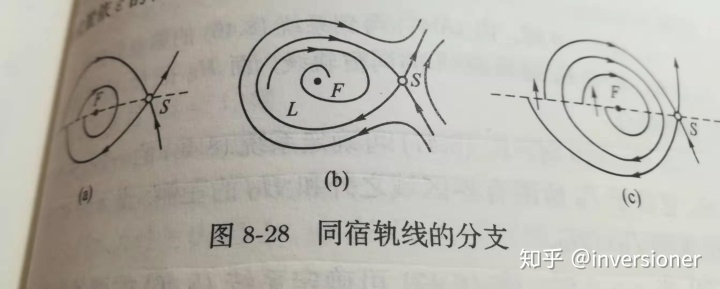
结点或焦点总是具有这样的性质：如果一条轨线趋向于结点或焦点，则经过充分接近这条轨线的点的另一条轨线也会有同样的归宿。然而，鞍点不具有这样的性质。如果一条轨线正向或负向趋于鞍点(此时称轨线为鞍点的分界线)，这无论取多么靠近分界线的点作为起始点，对应的轨线都总是趋于不同的地方。如果一条轨线两端都趋于鞍点，那么它很可能会在扰动下破坏结构。如果两端的鞍点是同一个点，称这条轨线为同宿轨线；否则称为异宿轨线。

下面是一些实例说明定理的条件是必要的。考虑系统

的扰动系统：

其中

为参数，且

，函数

连续可微。

如果对于任意

，都存在

使得扰动系统与

是

-邻近系统却不轨道拓扑等价，则系统不是结构稳定的。此时称

是扰动系统族的一个

分支值。所谓分支的意思是，当

连续变化到零时，系统的拓扑结构发生了突变。

1.高阶奇点的分支

这个例子说明，高阶奇点有时可以视为初等奇点的「复合」。

考虑动力系统

以及扰动系统族

。容易看出，当

时，扰动系统没有奇点；而

时，扰动系统有两个奇点

，一个是不稳定的两向结点，另一个是鞍点。当

时，两个奇点逐渐靠近。在

时发生了奇怪的现象：两个奇点似乎拼在一起成为一种新的奇点，这是一个高阶奇点。

鞍-结点

这样的点就像一个结点和一个鞍点的拼合，叫做鞍-结点。显然，这种拓扑结构不可能与它的扰动系统等价。所以，

是系统的分支值。我们把这种现象叫做

鞍-结点分支。

2.Hopf分支

考虑动力系统

以及它的扰动系统族

。扰动系统线性部分的矩阵有特征值

。由于

，故这个系统与线性化系统有相同的焦点且稳定性相同。当

的取值由负变为正时，焦点由稳定焦点变为不稳定焦点，从而

是系统的分支值。

下面进一步研究这些系统。用极坐标代换：

。则扰动系统族为

。由此可以发现，当

的取值由负变为正时，不仅奇点稳定性突变，而且从原点产生了一个极限环，随着

增大而逐渐扩大。这种分支现象叫做

Hopf分支。

3.Poincaré分支

这是一个与Hopf分支稍有不同的类型。

考虑系统

以及扰动系统族

。

原系统以

为中心点，所以每一个以此为圆心的圆都是它的闭轨。然而扰动系统不一样：当

时，系统以

为唯一闭轨，也就是极限环。(请大家证明)从而

是系统的分支值。与Hopf分支的不同之处在于，这里的极限环并不会收缩到奇点，而是趋于单位圆。这种扰动前是中心点的一条闭轨，扰动后不破裂而成为系统唯一闭轨的现象叫做

Poincaré分支。

4.多重闭轨的分支

考虑系统

，以及它的扰动系统族

。

对于

，用极坐标代换得到

。在

时，系统有两条闭轨

。在

内部和

外部恒有

，在

之间恒有

。从而这是仅有的两条闭轨，且一个是稳定极限环，另一个是不稳定极限环。在

时，二者拼合成一个半稳定极限环

，由之前的讨论知这是一个多重极限环，从而破坏了定理条件(2)。这种现象叫做

多重闭轨的分支。

5.同宿轨线的分支

我们需要构造一个例子：

，它有一个鞍点

。在

时有一条

的同宿轨线

，

内是稳定的初等焦点的吸引域。在

时同宿轨线破裂，成为两条分界线。由于图难画，我就直接拍照好了。

图中的情况c有一个极限环，事实上这是可以构造出来的，因为

充分小时取焦点的邻域以及分界线可以构造一个Poincaré-Bendixson环域。当

很小时这个极限环充分接近之前的同宿轨线

(因为环域可以充分接近)，所以可以看作是

扰动破裂之后产生的。这样的现象叫做

同宿轨线的分支。类似有 异宿轨线的分支，但是这里不讨论。下面正式构造这样的系统族。

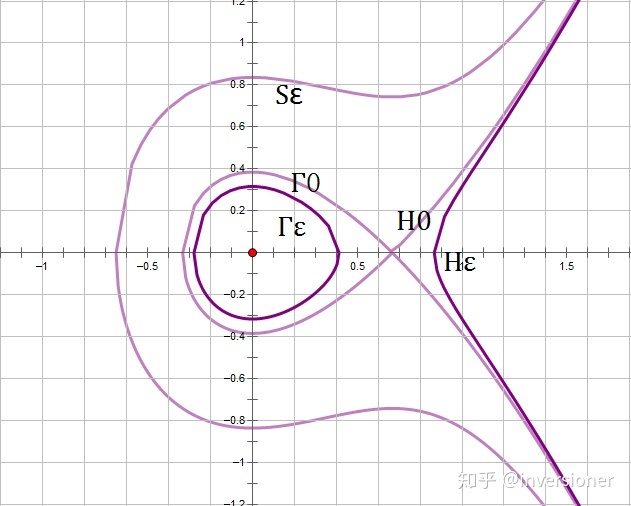
令系统

。它有两个奇点：

。由于这个方程组可以两式相除得到首次积分：

，故容易证明

是中心点，而

是鞍点。注意到

，我们考虑

。这样确定的曲线族长这样：

其中

是同宿轨线，

是另一条分界线。

是

时的轨线，而

是

时的轨线。当

时

;当

时

。令

，然后构造系统族

。计算出函数

关于该系统的全导数为

。这样在上图所示的区域内可以逐一确定全导数的符号(由于可以确定

的符号)。经过细致的讨论，我们可以确定在

时，系统的轨线族分别具有a,b,c三种结构，且

时扰动系统的极限环正是

。细节请大家完成。

参考

1. ^书上说的Lyapunov第一方法是用上一章的级数解来研究，但是这方法在Lyapunov之后几乎没有后续的发展，所以不讲。我也没有查到相关资料，就不说了。