双边功率谱密度和单边功率谱密度_功率谱密度(专业文章,勿膨者勿入)

来源：不忘初心的模拟小牛牛公众号

作者：131v1vv

在之前所发的 深入浅出聊抖动(Jitter)一文中我们着重学习了Jitter的时域相关内容，也遇到了很多各种各样的专业术语，有很多人被绕晕了。所以这里有必要再回顾一下频域相关的概念，算是一些补充知识吧。这期就围绕功率谱密度(Power Spectral Density，PSD)的概念展开。

先简单回忆一下图1中的任意实信号x(t)，及其扩展函数，绝对值|x(t)|和平方x^2(t)。如果是个电压或电流信号，我们可以得到能量Energy和功率Power的相关定义。如任意时间段的总能量，瞬时功率，平均功率等。

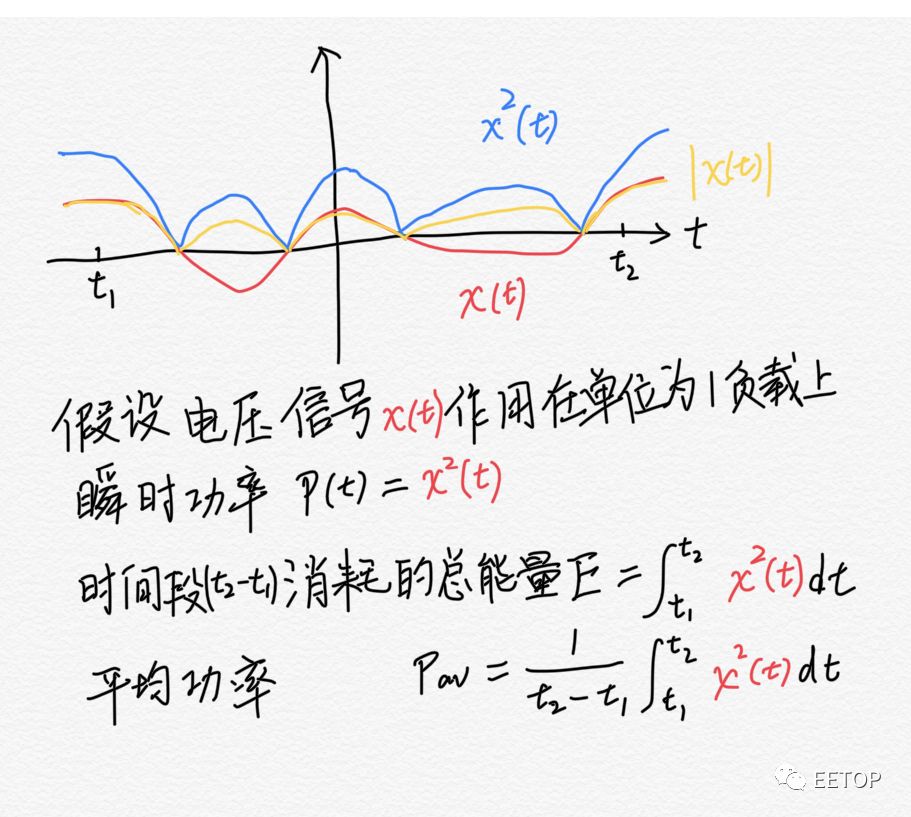
图1

而x(t)存在傅里叶变换的充分条件为，x(t)满足绝对积分(absolute integratable)且有有限个间断点。在频域存在着等效的表达式X(jω)。同时包含着幅度谱和相位谱。即存在傅里叶变换对，满足时域和频域的相互转换，且二者是等价的。

在存在傅里叶变换的条件下，根据帕萨瓦尔(Parsev