机器人关节空间轨迹规划--S型速度规划

• 关节空间 VS 操作空间

　　关节空间与操作空间轨迹规划流程图如下（上标$i$和$f$分别代表起始位置initial和目标位置final）：

 

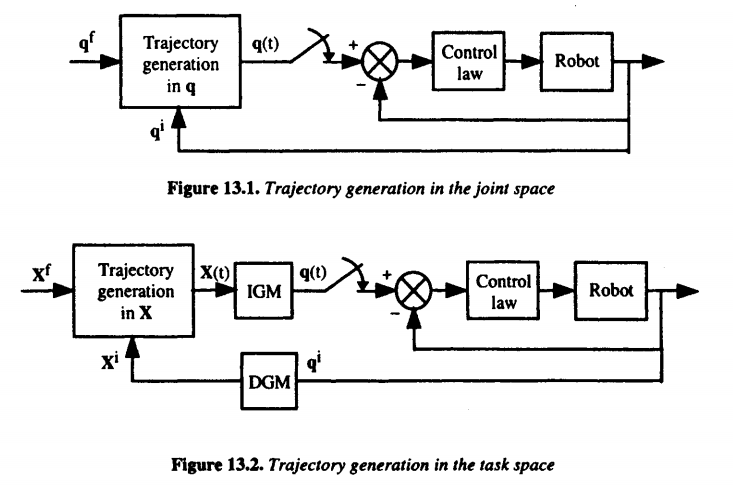
　　在关节空间内进行轨迹规划有如下优点：

1. 在线运算量更小，即无需进行机器人的逆解或正解解算
2. 不受机器人奇异构型影响
3. 可以根据机器人或驱动器手册直接确定最大速度或力矩

其缺点是对应操作空间的轨迹无法预测，增加了机械臂与环境碰撞的可能。例如，考虑下面的二连杆机构，关节运动的限制为：$0^{\circ} \le \theta_1 \le 180^{\circ}$，$0^{\circ} \le \theta_2 \le 150^{\circ}$

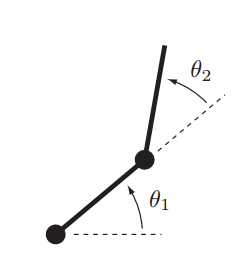
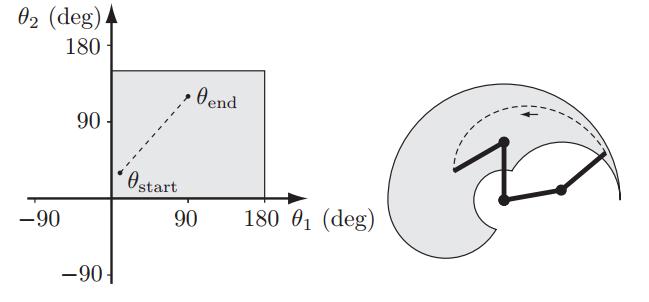
 　　下图中，左侧为关节空间内规划的线性运动轨迹，而其对应在操作空间的轨迹却是弧线。机构末端的可达空间在图中由灰色背景表示，其大小和形状受关节运动范围的影响。

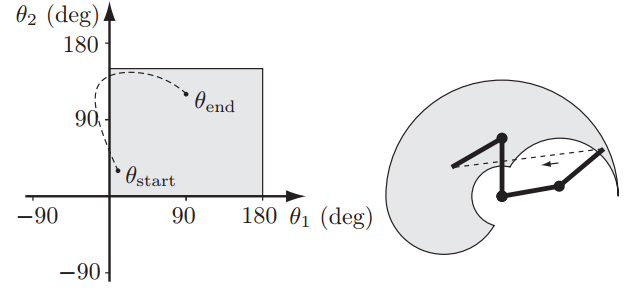
 　　下图在操作空间中规划了一条直线轨迹，其对应的关节空间轨迹为一弧线，且在运动过程中超出了关节值限制。操作空间内进行轨迹规划优点是直观，缺点是计算量大（需要计算逆解），会遇到奇异性问题以及关节运动超限等。

　　到底是选择在关节空间还是操作空间内进行轨迹规划，取决于任务需要。需要考虑避障或必须沿特定轨迹运动时选择操作空间轨迹规划，只需考虑速度、力矩、关节范围等运动约束时选择关节空间轨迹规划（The joint space scheme is appropriate to achieve fast motions in a free space）。

• 梯形速度曲线

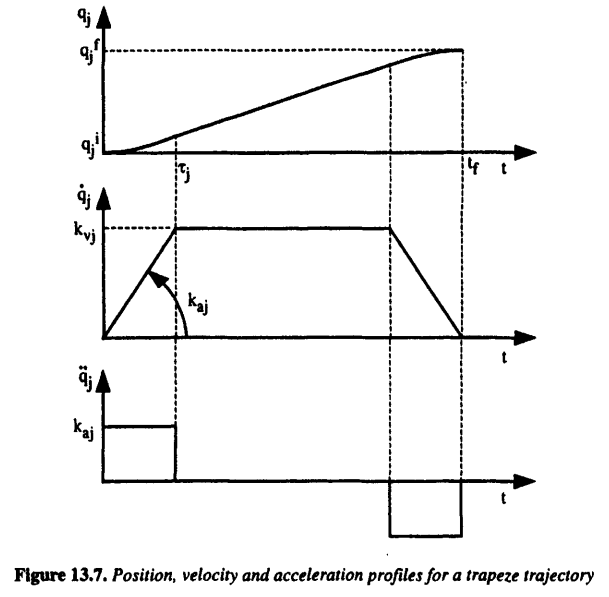
　　运动控制系统中常用的梯形速度曲线如下图所示，会出现加速度不连续的情形（从$k_{aj}$到0的跳变），这样可能会导致机械系统出现冲击或不可预料的振动，不过由于机械系统存在一定的弹性并不是绝对刚体，这种加速度不连续造成的冲击会被机械机构滤除或减轻。而对于高速重载的机器人来说，这种加速度不连续造成的影响就不能忽略了。可以参考知乎上这个问题：多轴插补为什么普遍使用梯形速度曲线？

•  S型速度曲线
  

 　　为了使加速度连续，可对梯形速度规划中的加速度曲线进行修改，使加速度曲线变为连续的二次曲线(a)或者梯形曲线(b)，如下图所示。其中，$\tau'$为加速段时间，$\lambda_jk_{vj}$为第$j$个关节的最大运动速度

 

　　下面考虑a方法（Linear Trajectory with Polynomial Blends），关节$j$的运动边界条件如下，即关节$j$初始时刻位置为$q_j^i$，初始速度加速度为0，$\tau'$时刻加速到最大速度$\lambda_ik_{vj}sign(D_i)$，$k_{vj}$为理论上关节$j$允许的最大速度，$\lambda_j$为一比例系数（$0 \le \lambda_j \le 1$），$D_j$为从起始位置到目标位置的位移，它是一个有正负的数值。

 

　　根据边界条件加速度二次曲线表达式为：$k(t-\tau')t$，对其进行积分，可得$\dot{q_j}(t)=\frac{1}{6}k(2t-3\tau')t^2+C$，根据速度边界条件可知$C=0$，$k=\frac{-6}{\tau'^3}\lambda_jk_{vj}$。于是推算出加速度、速度、位置的表达式分别为：$$\begin{cases}& q_j(t)=q_j^i-\frac{1}{\tau'^3}\lambda_jk_{vj}sign(D_j)(\frac{1}{2}t-\tau')t^3\\&\dot{q_j}(t)=-\frac{1}{\tau'^3}\lambda_jk_{vj}sign(D_j)(2t-3\tau')t^2\\&\ddot{q_j}(t)=-\frac{6}{\tau'^3}\lambda_jk_{vj}sign(D_j)(t-\tau')t  \end{cases}$$

　　加速度在$t=\tau'/2$时最大，其幅值为$\left |\ddot{q}_{jmax} \right |=\frac{3}{2}\frac{\lambda_jk_{vj}}{\tau'}=\upsilon_j k_{aj}$，则有：$$\tau'=\frac{3}{2}\frac{\lambda_jk_{vj}}{\upsilon_j k_{aj}}$$

　　根据上式和$q_j(t)$的表达式，可以计算出加速阶段的位移为：$$|q_j^i-q_j(\tau')|=\frac{3}{4}\frac{(\lambda_jk_{vj})^2}{\upsilon_j k_{aj}}$$

　　速度曲线与时间轴围成的面积为$|D_j|$，根据计算可以得到关系式：$$t'_f=\tau'+\frac{|D_j|}{\lambda_jk_{vj}}$$

　　在加速度为0的阶段（最大速度阶段，$\tau' \le t \le \tau'+h'$），关节速度表达式为：$$q_i(t)=q_j(\tau')+(t-\tau')\lambda_jk_{vj}sign(D_j)$$

　　减速阶段与加速阶段对称($t'_f=2\tau'+h'$)，减速阶段在时间段$\tau'+h' \le t \le t'_f$上的轨迹为：$$\begin{cases}&q_j(t)=q_j^f+\frac{1}{2}[\frac{1}{\tau'^3}(t-3\tau'-h')(t-\tau'-h')^3+(2t-3\tau'-2h')]\lambda_jk_{vj}sign(D_j) \\ &\dot{q_j}(t)=[\frac{1}{\tau'^3}(2t-5\tau'-2h')(t-\tau'-h')^2+1]\lambda_jk_{vj}sign(D_j)  \\  &\ddot{q_j}(t)= \frac{6}{\tau'^3}(t-2\tau'-h')(t-\tau'-h')\lambda_jk_{vj}sign(D_j)\end{cases}$$

　　如果目标点距离初始位置过近，可能达不到最大速度和加速度就要开始减速，考虑以最大速度做匀速直线运动阶段的时间为0这种临界状态（The minimum time $t_f$ is obtained when the parameters $\lambda_j$ and $\upsilon_j$ are the largest），为了能以最大速度运动，位移$|D_j|$必须满足如下条件：$$|D_j| > \frac{3}{2}\frac{k_{vj}^2}{k_{aj}}$$　　如果该条件不能满足，则最大速度值应为：$$k'_{vj}=\sqrt{\frac{2}{3}|D_j|k_{