MATLAB机械臂轨迹规划：在关节空间中生成多项式轨迹以及 jtraj函数（内容超详细讲解）

前言

此处为单关节在关节空间中生成多项式轨迹，利用MATLAB编程建立关节空间轨迹生成器，生成其关节空间的路径。

1、三次多项式

已知起始点和终止点的角速度为0；起始点角度值为120°，终止点角度值为60°；整个运动时间t=1s。根据公式: 进行计算，在MATLAB中编程运行生成三次多项式单关节轨迹，结果如图1所示：

图1 三次多项式轨迹生成图

2、五次多项式

已知起始点和终止点的角速度，角加速度均为0；起始点角度值为120°，终止点角度值为60°；整个运动时间t=1s，则根据公式: 进行计算，在MATLAB中运行生成五次多项式单关节轨迹曲线，结果如图2所示：

图2 五次多项式轨迹生成图

如图3所示，对比a)中三次多项式和五次多项式的结果可知，三次曲线在初始时刻和终止时刻时，加速度不连续、突变的，会存在冲击。而五次多项式的曲线加速度是连续的，可解决掉三次曲线存在的问题。

图3 三次多项式和五次多项式轨迹对比图

3、 两段带有中间点路径的三次

已知起始点为60°，中间点为120°、终止点为30°，起始点、终止点的速度和加速度为0，中间点t1=1，tf=2,中间时刻的速度不为0，因此在两条三次曲线的连接处，用速度和加速度均连续作为新的约束条件，并根据公式: 进行计算。在MATLAB中代码运行计算结果如图4所示，其仍存在三次多项式加速度不连续的冲击问题。
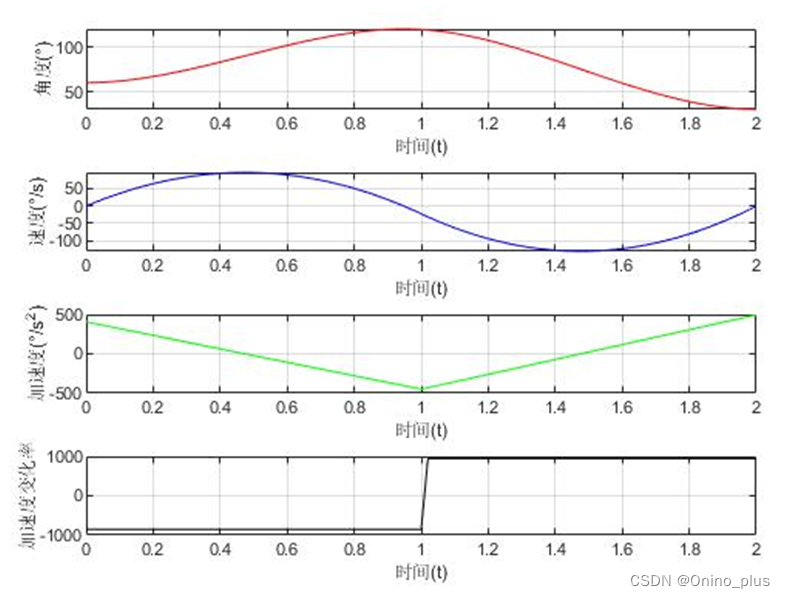图4 带中间点的三次多项数轨迹生成图

4、Jtraj()函数

利用Corke MATLAB机器人工具箱中的jtraj()函数，如图5所示，对比五次多项式，如图6所示，得出该函数的轨迹规划也是采用五次多项式插值法。

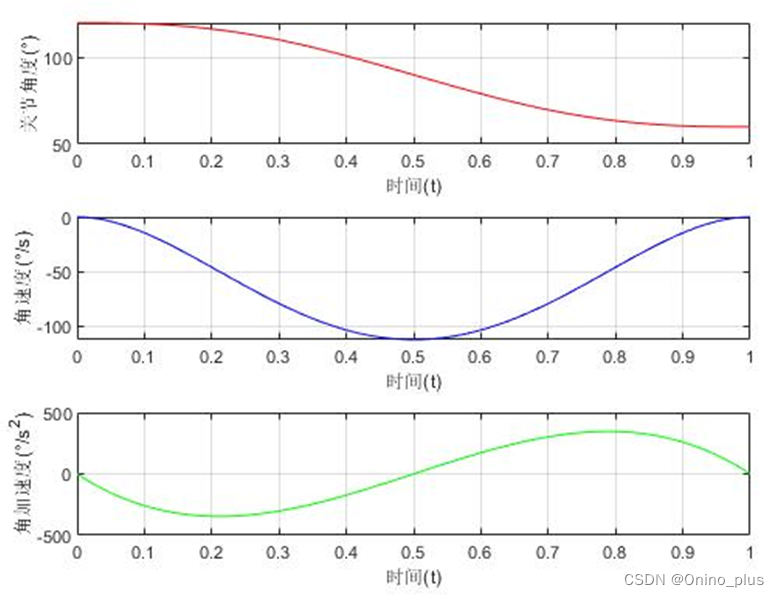
图5 jtraj函数生成的轨迹图

图6 五次多项式与jtraj函数生成对比图

附录：MATLAB运行代码

%% a)三次项多项式
clear;close all;clc;
figure('name','三次多项式');
q3_s = 120; q3_f = 60;
t3_s=0; t3_f = 1;
v3_s = 0;v3_f = 0;
%计算系数
a0_3 = q3_s;
a1_3 = 0;
a2_3 = (3/t3_f^2)*(q3_f - q3_s);
a3_3 = (-2/t3_f^3)*(q3_f - q3_s);
j = 1;
for tc = 0: 0.01: 1
   q_3(j) = a0_3 + a1_3*tc + a2_3*tc^2 + a3_3*tc^3; %角度变化函数
   qd_3(j) = a1_3 + 2*a2_3*tc + 3*a3_3*tc^2;%角速度
   qdd_3(j) = 2*a2_3 + 6*a3_3*tc;%角加速度
   qddd_3(j) = 6*a3_3;%加速度变化率
   j = j + 1;
end
subplot(4,1,1),plot([0:0.01:1], q_3,'r'),xlabel('时间(t)'),ylabel('角度(°)');grid on;
subplot(4,1,2),plot([0:0.01:1], qd_3,'b'),xlabel('时间(t)'),ylabel('速度(°/s)');grid on;
subplot(4,1,3),plot([0:0.01:1], qdd_3,'g'),xlabel('时间(t)'),ylabel('加速度(°/s^2)');grid on;
subplot(4,1,4),plot([0:0.01:1], qddd_3,'k'),xlabel('时间(t)'),ylabel('加速度变化率');grid on;

%% b五次多项式
figure('name','五次多项式');
a_array1 = 0;a_array2 = 0;%起止加速度值
t_array1=0;t_array2=1;%起止时间值
q5_s