梯形速度规划算法

梯形速度是运动控制系统使用的最简单的一种速度规划方式，其速度曲线如下图所示：

v0为初速度，vn为匀速运行速度，vt为末速度，加速和减速阶段加速度为a，总路程为S。

则加速阶段走过的路程S1=(vn*vn-v0*v0)/2a,减速阶段走过的路程S3=(vn*vn-vt*vt)/2a，

则匀速阶段走过的路程S2=S-S1-S2

若S2<=0，代表此时没有匀速阶段，此时梯形速度退化成下图：

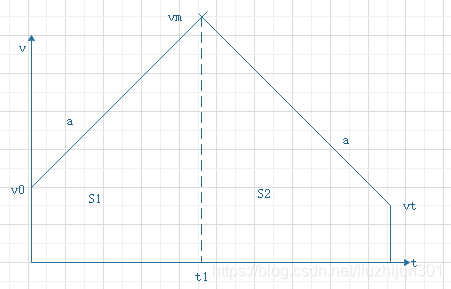
加速段和减速段相交点位最大速度Vm，由下列关系式成立：

则推导出：

带入算得：

                                               （1-1）

S1为加速阶段走过的总路程，若S1<0，代表没有加速阶段只有减速阶段，若S2>S，代表只有加速阶段没有减速阶段。

最后总结一下梯形加速度规划方案：

在规划函数中：

   

在速度生成函数中：