论文阅读笔记：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORK

arXiv:1609.02907v4

这篇论文笔记主要参考了

1.【GCN】论文笔记：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
2. 机器学习论文笔记-Semi-Supervised Classification with Graph Convolutional Networks
3. 从CNN到GCN的联系与区别——GCN从入门到精（fang）通（qi）

0.补充知识

使用神经网络模型$f(X,A)$ 对所有带标签节点进行基于监督损失的训练。

• $X$为输入数据
• $A$是图$G=(V,E)$的邻接矩阵
• $D$是顶点的度矩阵（对角矩阵），$D_{ii}={\sum }_j{A}_{ij}$
• (Laplacian 矩阵, Combinatorial Laplacian): $L=D-A$
• (Laplacian 矩阵, Symmetric normalized Laplacian): $L^{sys}=D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$
• (Laplacian 矩阵, Random walk normalized Laplacian): $L=D^{-1}L=I_N-D^{-1}A$

1.INTRODUCTION

图半监督学习的目标是，在给定的图结构的数据中，少部分节点是有标记的，大部分节点是未标记的，预测出未标记节点的标签。
经典的方法：

• 基于平滑正则，即假设相邻的节点具有相似的label–[Zhu et al., 2003]：$\mathcal{L}={\mathcal{L}}_0+\lambda {\mathcal{L}}_{reg}$,
  ${\mathcal{L}}_{reg}={\sum }_{i,j}{A}_{ij}\Vert f(X_i)-f(X_j){\Vert }^2=f(X{)}^T\left(D-A\right)f(X)$

2.Graph中的快速卷积

图卷积网络（GCN）的每层表达式为
$$H^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right)$$
其中

• $\tilde{A}=A+I_N$
• ${\tilde{D}}_{i,i}={\sum }_j{\tilde{A}}_{i,j}$
• $\sigma (\cdot )$为激活函数
• $W^{(l)}$ 为学习参数

原始方法

定义谱方法的图卷积为
$$g_{\theta }\star x=U{g}_{\theta }{U}^{T}x$$.
其中

• $g_{\theta }=diag(\theta ),\theta \in {\mathbb{R}}^N$
• $L=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}=U\Lambda U^T$ ，$U$为$L$的特征向量，相应的$\Lambda$为特征值的组成的对角阵，两者相互对应。

Chebyshev多项式逼近法

[Hammond et al., 2011]将$g_{\theta }(\Lambda )$用Chebyshev多项式$T_k(x)$逼近:
$$g_{{\theta }^{{}^{\prime }}}(\Lambda )\approx \sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(\tilde{\Lambda }),\tilde{\Lambda }=\frac{2}{{\lambda }_{max}(\Lambda )}\Lambda -I_N$$
因此得到Chebyshev多项式逼近图上谱卷积为：
$$\begin{array}{rl}{g}_{{\theta }^{{}^{\prime }}}\star x& \approx U\left(\sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(\tilde{\Lambda })\right)U^{T}x\\ & =\sum _{k=0}^K\left(U{\theta }_k^{{}^{\prime }}{T}_k(\tilde{\Lambda })U^T\right)x\\ & =\sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k\left(U\tilde{\Lambda }{U}^T\right))x\\ & =\sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(\tilde{L})x\end{array}$$
其中$\tilde{L}=\frac{2}{{\lambda }_{max}(L)}L-I_N$。

Chebyshev多项式逼近法简化

如果取${\lambda }_{max}\approx 2$则有$\tilde{L}=L-I_N$。Chebyshev多项式只取前两项，即$K=1$ 有
$$\begin{array}{rl}{g}_{{\theta }^{{}^{\prime }}}\star x& \approx \left({\theta }_0^{{}^{\prime }}+{\theta }_1^{{}^{\prime }}(L-I_N)\right)x\\ & =\left({\theta }_0^{{}^{\prime }}-{\theta }_1^{{}^{\prime }}{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\right)x\end{array}.$$

单参数法

令参数${\theta }_0^{{}^{\prime }}=-{\theta }_1^{{}^{\prime }}=\theta$，图上谱卷积又可以简化为
$$g_{{\theta }^{{}^{\prime }}}\star x\approx \theta \left(I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\right)x$$

注意$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$拥有范围为$[0,2]$的特征值，这将会导致数值不稳定性和梯度爆炸/消失。因此我们介绍下面的归一化技巧(renormalization trick)：
$$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}.$$
其中$\tilde{A}=A+I_N,{\tilde{D}}_{i,i}={\sum }_j{\tilde{A}}_{i,j}={\sum }_j\left(A_{i,j}+(I_N{)}_{i,j}\right)=D_{i,i}+1$。上式展开为
$$\begin{array}{rl}{I}_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}& \to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}\\ & =(D+I_N{)}^{-\frac{1}{2}}(A+I_N)(D+I_N{)}^{-\frac{1}{2}}\\ & =(D+I_N{)}^{-\frac{1}{2}}A(D+I_N{)}^{-\frac{1}{2}}+(D+I_N{)}^{-1}\end{array}.$$

推广

输入$X\in {\mathbb{R}}^{N\times C}$，$C$为输入的通道数，经过滤波$\Theta \in {\mathbb{R}}^{C\times F}$得到含有$F$个通道的卷积后结果$Z\in {\mathbb{R}}^{N\times F}$：
$$Z={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}X\Theta$$

3.半监督节点分类

上图中，左(a)是一个GCN网络示意图，在输入层拥有$C$个输入，中间有若干隐藏层，在输出层有$F$个特征映射；图的结构（边用黑线表示）在层之间共享；标签用$Y_i$表示。右(b)是一个两层GCN在Cora数据集上（使用了5%的标签）训练得到的隐藏层激活值的形象化表示，颜色表示文档类别。

考虑一个用于半监督图节点分类问题的两层GCN，邻接矩阵为$A$（二进制/加权）。

预处理

计算$\hat{A}={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$,模型则为:
$$Z=f(X,A)=softmax\left(\hat{A}ReLU\left(\hat{A}X{W}^{(0)}\right)W^{(1)}\right)$$

交叉熵

评估所有带标签的节点集${\mathcal{Y}}_L$的交叉熵误差：
$$\mathcal{L}=-\sum _{l\in {\mathcal{Y}}_L}\sum _{f=1}^F{Y}_{lf}\ln (Z_{lf})$$

训练

网络中的权重$W^{(0)}$和$W^{(1)}$通过梯度下降训练。我们对每个【训练迭代】使用完整的数据集执行【批量梯度下降】，这是一个可行的选择，只要数据集适合内存。对于$A$使用稀疏表示，即边数是线性的。通过Dropout引入训练过程中的随机性。我们将内存效率扩展与小批随机梯度下降留作以后的工作。

5.实验

• 引文网络：半监督文档分类
• 从知识图中提取的二分图：半监督实体分类

5.1数据集

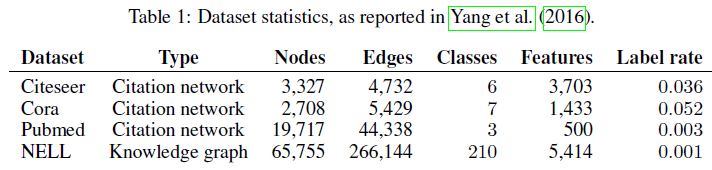
实验参数

• 使用3.1节中的两层GCN网络
• prediction accuracy：1000张带标签测试集
• 对比实验：十层网络
• 使用500张带标签验证集：超参数的初始化、所有层的dropout率、第一层的L2正则化因子、隐藏层单元的个数

引文网络数据集

• 最大200迭代期
• Adam算法
• 学习率为0.01
• 停止条件：验证集loss连续十个迭代期没有下降
• 权重初始化方法：Xavier
• （按行）对输入特征向量归一化

随机图数据集

• 隐藏层32个单元
• 省略dropout和L2正则化

6.结果

四个常用的数据集，三个citation networks和一个knowledge graphs，都取得了不错的效果。

CPU和GPU上的训练时间：

对比不同的卷积逼近方式，作者提出的归一化技巧(renormalization trick)这种方式优势明显，表现优异：

模型深度对性能的影响，可以看出，3层左右的时候效果比较好。