均值与平均值的关系_量子力学笔记7波动力学力学量的平均值

2.5 力学量的平均值

2.5.1 位置的平均值

      既然 |ψ(x, t)|2 是粒子在空间出现的概率密度，它就是一个通常所谓的“分布函数”，我们可以用它来求力学量 F(x) 在空间的平均值。例如，对于最简单的情况 F(x) = x，粒子坐标的 x 的平均值为

      这个表达式就普通概率论中的平均值公式。

      需要注意的是这里的平均值是多次对相同的系统测量得到位置的平均值，而不是对一个系统重复测量的平均值。因为一旦测量，这个事件就发生了，即概率为 1。数学上就是第一次测量之后波函数就塌缩成 δ 的函数，只要足够快，之后的测量仅仅是重复同样的值。

2.5.2 动量的平均值

      波函数 ψ(x, t) 随时间改变，概率密度 ρ(x, t) = |ψ(x, t)|2 当然随时间改变，ρ(x, t) 是空间和时间的二元函数。坐标的平均值

      对 x 积分后是时间的函数，故坐标的平均值 ⟨x⟩ 也会随着时间的改变。坐标的平均值 ⟨x⟩ 随时间改变到底有多快呢？从数学上说，我们就对这个时间函数求导；从经典物理上看，就是求速度。即

      其中利用了(2.33)式，并用到了分部积分和波函数在无限远处为零

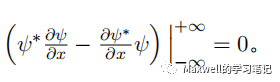
      速度的平均值等于位置平均值的时间导数

      这样，如果已经求到了位置的平均值，再求动量平均值就很方便。

2.5.3 力的平均值

      对于一个动量为 p，势能为 V (x) 的微观粒子，经典力学的基本方程

依然成立。其中，⟨p⟩ 是动量的期望值，而 ⟨−∂V/∂x ⟩ 是力函数

的平均值。

证明：

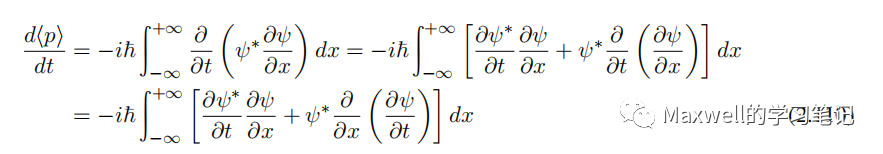
      其中

      由薛定谔方程，有

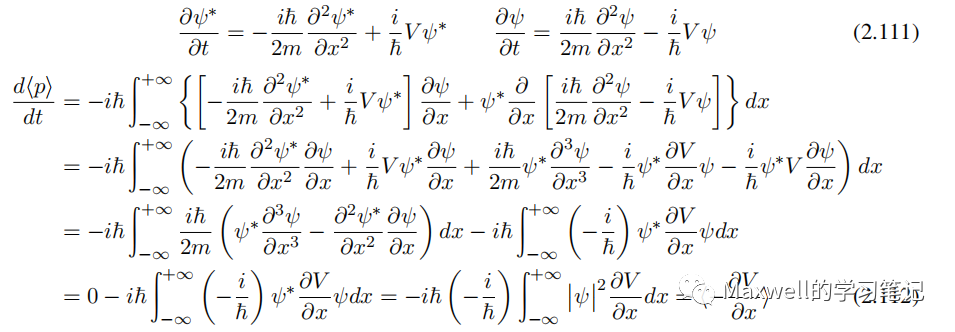
      其中

即

得证。

      这个结果表明，在量子体系中力学量的期望值的变化遵从经典定律，它是埃伦费斯特定理(Ehrenfest’s theorem)的一种特殊形式(在力学量随时间的演化我们将推导)。这个定理意味着，由量子行为向经典退化的一个途径是取力学量的期望值。

2.5.4 力学量在任意态中的平均值

2.5.4.1 分立谱

      在厄米算符的本征函数的正交性和完备性的讨论中，我们知道，若ψ1(x), ψ2(x), · · · , ψn(x), · · ·是厄米算符Fˆ 的归一化本征函数，相应的本征值为λ1, λ2, · · · , λn, · · · 它们满足本征方程F ψˆn(x) =λnψn(x)，则本征函数服从正交关系式

      一定要对完备性，要有深刻理解。而任一连续函数 f(x) 可以按本征函数系 {ψn(x)} 展开为

其中，展开系数

是复常数。现在我们考查展开系数 cn 的物理意义。设 f(x) 已经归一化，利用 ψn(x) 的正交关系，有

      由这个结果可以看出，|cn|2 具有概率的意义。先考虑一个特殊情况，如果 f(x) 是算符 Fˆ 的某一个本征态，如 f(x) = ψN (x)，则上式右边的求和中除 |cN |2 = 1 外，其余都等于零。在这种情况下测量力学量 F，必定得到确定的结果 λN。一般情况下，c2n 表示任意态 f(x) 中发现本征态 ψn(x) 的概率(体系处于本征态 ψ1(x)，ψ2(x)…，ψn(x)，…的概率之和为 1)。换言之，|cn|

2 表示在 f(x) 态中测量力学量 F 得到本征值 λn 的概率。由此，cn 通常被称为“概率幅”，这是量子力学中一个非常重要而有趣的概念。测量到的都是本征态。每次对量子系统测量只能测到本征态 n 的本征值 λn，但是测到的概率为 |cn|2，而多次测量的平均值为

      基于上述讨论，我们引进有关力学量算符表示的另一个基本假设：量子力学中表示力学量的算符 Fˆ 是厄米算符，它们的本征函数构成完备集。当体系处于任意波函数 f(x) 所描述的状态时，力学量 F 没有确定的数值，而是有一系列可能的值，这些值就是算符 Fˆ 的本征值λ1, λ2, · · · , λn, · · · 测量力学量 F 得到本征值 λn 的概率是 |cn|2。这样一来，力学量 F 在任意态f(x) 中的平均值便是

它具有统计平均的形式，可以一般性的简化为

证明：事实上，我们有

      现在我们可以看出，力学量 F 在任意态 f(x) 中的统计平均值就是算符 Fˆ 在这个态中的期待值。利用上式可以直接从算符 Fˆ 和体系所处的状态 f(x) 得出力学量 F 在这个状态中的平均值。如果体系的状态 f(x) 就是算符 Fˆ 的一个本征态 ψn(x)，则给出

这时力学量 F 的平均值就是确定的本征值 λn。

2.5.4.2 连续谱

      如果 Fˆ 的本征值组成连续谱，则相应的本征方程为

这时本征值 λ 取连续变化的实数。本征函数的正交关系式变为

任意态 f(x) 按本征函数集 {ψλ(x)} 的展开则表示为对本征值 λ 的积分

其中，c(λ) 为连续谱情况下的概率幅。为求 c(λ)，对(2.126)式两边同乘以

然后对 x 积分，并利用正交关系(2.125)，得

即

      它与分立谱情况下的概率幅有相同的形式。有

      这个结果表示，|c(λ)|2 具有概率密度的意义。事实上，|c(λ)|2 是任意态 f(x) 中发现本征态 ψλ(x)的概率秘密。换言之，它是在 f(x) 态中测量力学量 F 得到 λ 的概率密度。于是力学量 F 在 f(x) 态中的平均值为

在连续谱情况下，依然可以用式

      我们现在考虑一种重要的特殊情况，即 Fˆ 为一维动量算符：

                                       Fˆ = ˆpx = −iℏ∂/∂x，

动量本征函数为

则概率幅为

是 f(x) 的傅里叶变换。可见在动量本征函数情况下，概率幅 c(p) 本征上是波函数 f(x) 的傅里叶变换。由连续谱的一般性结果可知，|c(p)|2 是动量概率密度。由此 c(p) 可以称为动量空间的波函数，简称动量波函数。关于 |c(p)|2 是动量概率密度的结论，我们可以从傅里叶变换关系式Plancherel 定理去论证。Plancherel 定理表示为

      设 f(x) 表示归一化的量子力学波函数，则

      利用(2.133)，并注意到 ω = p/ℏ，得

可见 |c(p)|2 确实是动量概率密度。

2.5.5 埃伦费斯特定理

2.5.5.1 基于薛定谔方程的推导

      埃伦费斯特定理(Ehrenfest’s theorem)描述是力学量的平均值随时间的演化。

证明：直接利用薛定谔方程证明。

      设一个量子体系在任意 t 时刻的状态由归一化波函数 ψ(t) 来描述，则任意一个力学量 A 的平均值为

等式两边对时间求导，有

利用薛定谔方程：

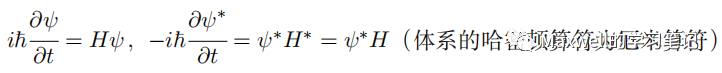
有

得证。

      可以看出时间偏导的平均值 ⟨∂A/∂t ⟩与平均值的时间偏导d⟨A⟩/dt 是明显不同的。而且平均值是如此重要，因为我们在实验中测得的数据可以都是平均值。于是平均值随不随时间变化于是变得很重要。如果算符 A 与时间 t 无关(不显含时间)，则∂A/∂t = 0，于是力学量的平均值随时间演化方程(2.137)式简化为

这个方程称为海森堡运动方程(Heisenberg motion equation)。

2.5.5.2 基于刘维尔—冯诺依曼方程的推导

      可以利用刘维尔方程来计算一个不显含时间的物理量 A 在混合态中的平均值 ⟨A⟩ 随时间的变化

其中

这就是开头讲的恩费斯特公式。

2.5.5.3 位置、动量和力的平均值关系

      利用埃伦费斯特定理

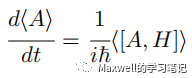
位置与动量平均值、动量与力的平均值的关系可以轻松求得。

证明：

(1)由

有

同理，y、z 方向也有同样结果，于是

(2)由

有

得证。

      可见量子力学中的平均值的运动方程

是符合牛顿力学方程的。

2.5.6 位力定理

      位力定理(Virial theorem)描述的是当体系处于定态下与动能相关的平均值。

证明：

(方法一)利用埃伦费斯特定理证明。

      设粒子处于势场 V (r) 中，哈密顿量 H 表示为

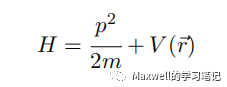
      考虑 ⃗r · ⃗p 的平均值随时间的变化，利用埃伦费斯特定理，

有

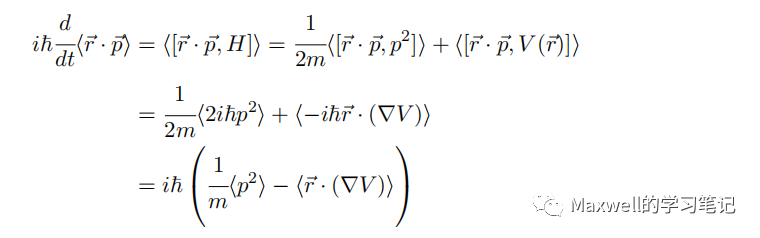
对于定态，

有

式中

为粒子动能。

(方法二)利用变分法和标度变换证明。

      作标度变换，令 ⃗r → ⃗r′ = λr，则 ⃗p = −iℏ∂/∂⃗r = λp′，于是动能为

      注意到归一化条件与标度变换无关，有

由变分原理，有

其中将 λ 看成变量，∂⃗r/∂λ = −⃗r′/λ2。当 λ = 1 时，r = ⃗r′，得

得证。

对于位力定理，存在很多特例。

2.5.7 赫尔曼—费曼定理

      借助于赫尔曼—费曼定理(Hellmann-Feynman thorem)可以得出关于各种力学量平均值的许多信息，而不必再利用波函数去进行繁琐的计算。设体系的哈密顿量 H 中含有某参量 λ，即，H(λ)，En 为 H 的本征值，相应的归一化本征函数为 ψn (n 为一组完备量子数)，则

      证明：由能量本征方程

对参量 λ 取导数，有

左乘 ⟨ψn|，得

利用 ⟨ψn|H = En⟨ψn|，有

即

得证。