傅立叶级数和傅立叶变换简介
用正确的方式打开傅立叶公式,才能理解它们,不需要死记。
在傅立叶分析里,我们能简单地看到两组公式。一组是傅立叶变换公式和傅立叶逆变换公式:
![]()
,
![]()
;
另一组傅立叶级数公式:
![]()
,
其中
![]()
,
,
。
看着这两组式子是挺玄的,虽然看不懂其中的含义,但是看着这两组式子是挺美的。在第一组式子中,首尾相关,一个
![]()
,一个
![]()
这两个东西,一个在里面一个在外面,从第一个公式到第二个公式,
![]()
、
![]()
就是换一下位置,多一个
![]()
,
![]()
的指数加上一个负号,后面的
![]()
换成
![]()
,就是第二个式子了。内外替换,稍作改变,然后公式还是成立的,这太神奇了吧。
在第二组公式中,好端端的一个公式就毫无理由地化成了毫不相干的一组三角函数的求和。
你感叹了公式的一番美好和伟大,然后还是没有看懂,同样也记不住这个公式,不理解其中的含义,更不会用这个公式。另外你之前学习傅立叶公式的时候,接触了大量的名词,这些名词同样不知云何来,不知哪里去。那我们这里先不讲这些明细,因为在傅立叶公式被创造的时候,是先创造的公式,其他的名词是为了使傅立叶公式更加准确后来才加上去的。
然而理解、认清并学会运用这个高大上的公式就是我们要解决的问题。我希望你能给自己半小时或三刻钟的时间,静下心来和我一起理解这个公式,就是这两三刻中的时间,你将会理解透彻,在收获(理解并深刻地记住)一个伟大的思想之外,并对这个伟大思想是如何生成的有所了解。
傅立叶公式并不是数学家凭空想出来,也不是灵感突袭想出来的,而是有历史可循,在其他数学工作基础上演变出来的。你可能会感到很意外,傅立叶分析是从我们高中就熟悉的低维度向量空间一步一步演变出来的。
下面我们以以下几步来学习傅立叶公式:三维空间——
![]()
维空间——无限维空间——希尔伯特空间——傅立叶级数——傅立叶变换。
你最不熟悉的是希尔伯特空间,不要被吓住,其实希尔伯特空间并不难,理解他的内容非常简单。只是这个名字是用大数学家希尔伯特的名字来命名的,并不是对该空间的描述,所以你还不知道什么是希尔伯特空间。那我们说,希尔伯特空间其实就是由三维空间到任意
![]()
维空间的拓展,并且,任意
![]()
维空间的向量的分解和组合和三位空间向量的方式一样,这样一说或许你就放心了。但是任意
![]()
维空间还不是希尔伯特空间,把任意
![]()
维空间和我们熟知的连续空间联系起来的无限维空间,这个无限维空间就是所说的希尔伯特空间。
傅立叶变换由傅立叶级数演变而来,傅立叶级数其实由希尔伯特空间而来,希尔伯特空间由任意
![]()
维空间而来,任意
![]()
维空间的空间性质和
![]()
维空间的性质一样,其实我们用到的性质只有两个:正交向量基和向量分解。我们一步一步来:
三维空间——
![]()
维空间——无限维空间——希尔伯特空间——傅立叶级数——傅立叶变换
三维空间里的正交单位向量基和向量分解
在三维向量中,我们常用的就是笛卡尔创立的空间直角坐标系,我们说的三个坐标轴上的正向单位向量就一组向量基。注意向量基的“基”字,它表示这是其他向量的基础,其他向量都可有这一组向量基进行表示。这一组是
![]()
,任何一个向量都可以用这组基来表示。例如
![]()
,
![]()
。任意三个不在同一平面上的非零向量都可以做作三维空间的一组基。记住,3 维空间要有 3 个基,3 个基都是非零的,而且不能在同一平面上。若在同一平面上,那它们就可以相互表示来,基是不能相互表示的,要是第三个向量基可以用前两个基表示,即是说第三个基可有可无,不要也行,但是一组基中的任何一个都是必须存在的,不能是可有可无的,所以基向量之间不能相互表示。两个向量不能相互表示就是两个向量线性无关。
在三维空间,有无数组基向量,只有
![]()
是最直观,最容易计算,最容易表示出来的。而且任意两个基都是相互垂直的,相互垂直的基的内积为 0 ,即
![]()
,
![]()
,
![]()
。另外,每个基的摸都为 1 ,即
![]()
,
![]()
,
![]()
。
、
、
线性无关,又相互垂直,而且每个基的摸都为 1 ,由这样一组基组成的基称为直交单位向量基。
你能直接看出来
![]()
,但是你也得知道是怎么算出来的,因为,到了高维空间,我们还是需要这些知识。假如,一开始你不知道
![]()
和
、
、
![]()
的关系,那我们假设
![]()
,现在我们的目标是 求解
![]()
、
![]()
、
![]()
是多少。
另外我们得知道
![]() 、
、
![]() 、
、
![]() 的含义,它们分别是
的含义,它们分别是
![]() 在三个基向量上的投影。
在三个基向量上的投影。
其中
![]()
,
![]()
与一个单位基向量相乘的内积就是
![]()
在该单位基向量上的投影的长度。
一般的,
是
在该单位基向量
上的投影的长度。
要是写成求和的形式:
,其中:
![]()
(每个基向量都是单位向量),
![]()
(任意两个基向量内积为0 ,相互垂直),
![]()
(
![]()
在该单位基向量
![]()
上的投影),
![]()
。
维空间里的正交单位向量基和向量分解
一个
![]()
维空间里的向量
![]()
,在
![]()
维空间里有一组直角单位向量基
![]()
;并且对于
且
![]()
,都有
![]()
(每个基向量都是单位向量)和
![]()
(任意两个基向量内积为 0 ,相互垂直)。
那么
![]()
在该单位基向量
![]()
上的投影的长度是
![]()
,由于这组向量基是直角单位向量基,这里求得的
![]()
就是
![]()
向量分解表达式中的
![]()
。
那么:
写成求和的形式:
,其中:
![]()
(每个基向量都是单位向量),
![]()
(任意两个基向量内积为 0 ,相互垂直),
![]()
(
![]()
在该单位基向量
![]()
上的投影),
![]()
。
我们很难想象出高于三维的空间,连四维空间都是难以想象出来的。四维已经很艰难,那更高的
![]()
维怎么办呢?我们根据求和公式
![]()
,把向量表示成一个不准确的形式:在每个单位基向量并排地放在一条线上,用柱高表示在该单位基向量上的分量。你可以看到
在
![]()
上的分量是
![]()
,在
![]()
上的分量是
![]()
,···,在
![]()
上的分量是
![]()
,它们依次排列在一条直线上。
![]()
表示
![]()
,在图上显示为每个分量的高度的平方和。希望你能够理解,这个理解方式帮助我们分析无限维空间。
我必须再重申重要的两个点:(1),任何一个基向量的模为
![]()
,任两个基向量内积为零;(2),
![]()
是
![]()
在该单位基向量
![]()
上的分量值。
希尔伯特空间里的正交单位向量基和向量分解
在
![]()
维空间中,如果这个
![]()
无限大呢?那该怎么办呢?这也是大数学家希尔伯特思考的问题。
我们很容易想象出,在无限维空间里,有一个向量有无限多个元素
,同样有一个拥有无限个元素的单位向量基
![]()
。
也很容易得出结论是:
![]()
,其中: 是
![]()
在该单位基向量
![]()
上的分量。
但是如果只到这为止,我们也没有必要把无限维空间称作希尔伯特空间了。希尔伯特还在思考另外一些问题。我们在
![]()
维空间中提到的都是点元素,是离散的,但是我们遇到的函数多是连续的,在连续和离散之间有一个巨大的鸿沟无法跨越,而希尔伯特就是尝试跨越这条鸿沟的人,他在思考如何在离散空间和连续空间两者之间建立联系的桥梁。其实,无限维空间就是这座桥梁。
设一个向量为一个向量函数
![]()
,这个向量函数到底是什么我们先不过问,现在仅把它当作一个无限维空间里的向量。同样有一组无限维空间里的直角坐标系为
![]()
、
![]()
、
![]()
、···。每个单位基向量都是一个单位函数向量,令
![]()
为
![]()
在
![]()
方向的投影,那
![]()
为
![]()
在
![]()
方向的投影;可得出:
即
![]()
。我们也可以形式地写出
![]()
。
在上面的过程当中,我们规定了一个向量函数
![]()
,但是我们想要的是一个连续函数,还不是向量函数,那该怎么办呢?我们同样面临着其他问题,如果我们把
中的向量性质去掉的话就是
![]()
,那我们如何界定
![]()
的模长呢,如何界定
![]()
、
![]()
、
![]()
、···是“单位函数”的呢,又如何界定它们之间“相互垂直”或者乘积为 0 的呢,再者,如何界定
![]()
在
![]()
、
![]()
、
![]()
、··· 上的分量呢?
在
![]()
维空间中,我们把
![]()
在各个方向上的分量并排地放在一条长度有限的线段上,并用
![]()
表示模。
![]()
越大,切的就越多,切之弥多,割之弥细;当
![]()
无限大的时候,每个柱子就细得没有宽度了,是一条竖线。我们把这无数条竖线集中在区间
![]()
上。如果这无数条竖线的上界是一条光滑的曲线的话,我们就可以称这条光滑的曲线是连续函数
![]()
的图像,线上一点的
![]()
值是该函数在该点所代表的方向上的分量。注意,我们这里界定了函数所在的区间,以后我们界定模和内积时也是在某个区间上进行界定。
函数的模。在无限维向量空间中,用各个方向上分量的平方和的开方
![]()
表示模。因为对于函数积分有着求和的作用,那我们对
![]()
在区间
![]()
上对各个“方向分量”的平方积分,再开方
![]()
表示模。
对于基函数
![]()
、
![]()
、
![]()
、··· 模的形式也是如此,
若
,我们就称该基函数为单位基函数。
另外需要注意的是:无限维向量空间是离散空间,我们用求和公式表示向量模,然而希尔伯特空间是连续空间,不能再用求和,需要用积分表示函数的模。从无限维向量空间到希尔伯特空间的跳跃,其中最重要的一步就是:把求和转换成积分。
两个函数的垂直。在无限维空间中,向量
![]()
和
![]()
垂直,那么它们每个相同方向的分量的乘积的求和为 0 :
![]()
。在希尔伯特空间中,
![]()
、
![]()
相互垂直,那它们在每个相同方向的分量的乘积的积分为0,在
这一点所代表方向上分量分别是
![]()
、
![]()
,乘积为
![]()
,那积分为
![]()
。
由此可知,两个函数
![]()
、
![]()
,
相互垂直,则
。
函数在单位基函数的分量。在无限维空间中,向量
![]()
在单位向量
![]()
上的分量记作
![]()
,
![]()
。
在希尔伯特空间中,
在
上的分量为
,同理,将向量中求和换成函数中积分的形式,有
。
如果有这样一组基函数
![]()
、
![]()
、
![]()
、
···,在区间 (a,b)
上,每个基函数的模都为 1,即
,每两个基函数都直交,即
,那我们称这样的一组函数为单位直交函数系。这个概念相当于向量中的单位直交基向量组。
向量所在的无限维空间我们称之为无限维向量空间,函数所在的无限维空间我们称之为希尔伯特空间。我们总结如下。
在希尔伯特空间中,函数
![]()
的模记作
![]()
:
![]()
;
两个函数
![]()
、
![]()
的内积为:
![]()
;
它们的角的余弦为
![]()
;
函数
![]()
在函数
![]()
的分量为:
![]()
即
![]()
;
函数
![]()
在单位函数
![]()
的分量为:
![]()
。
如果你能理解这些概念,那就太好了;如果不能,请再阅读一遍。希尔伯特空间的知识都是从无限维向量空间推理过来的,两个都是无限维空间,只不过希尔伯特空间的对象是函数,无限维向量空间的对象是向量。理解了上面的总结,下面的推论将会顺风顺水,一马平川。
我们知道,在无限维函数(希尔伯特)空间中,需要无限个单位基函数,而且两两正交,那有没有无数个这样的基函数呢?确实有,在三角函数中可以找到。我们在区间
![]()
找到这样一组函数系:
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,···,
![]()
,
![]()
,···。
你会发现区间
![]()
上它们中任意两个基函数乘积的积分为
![]()
,即任意两者相互直交:
![]()
。
另外,它们在区间模的长度为多少?
![]()
;
![]()
;
![]()
。
它们的模在区间
![]()
既然不为1,那它们除以自身的模后模就为 1 了。于是得到一组单位直交函数系:
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,···,
![]()
,
![]()
,···,
它们相互直交,而且每个模为1 。这个是历史上最早产生的也是最重要的直交函数系。
我们得到一组直交函数系,在区间
![]()
上目标函数
![]()
在该直交函数系上的分量如何?注意,这是一组在区间
![]()
上的直交函数系,有区间限制,所以,目标函数也必须在区间
![]()
上。
函数在基函数
![]()
上的分量为
![]()
;
在基函数
![]()
上的分量
![]()
;
在基函数
![]()
上的分量
![]()
。
就像
![]()
一样,我们有:
写成求和形式:
这就是傅立叶级数最初的形式,是在希尔伯特空间生成的。公式的推理并不复杂,关键是在能够完成从无限维向量空间到希尔伯特空间的跳跃。
把
![]()
,
![]()
,
![]()
带入式子有:
令
![]()
,
![]()
,
![]()
,这里统一了它们的形式,就有了
你所见的傅立叶级数:
,
其中
![]()
,
![]()
,
。
傅立叶级数怎么跳跃到傅立叶变换
这一块我还没有写,编辑公式很费劲,你先想想。
想不好再联系东雀dongquelaoshi@126.com。
另外,你肯定对上述很多内容不满意,不满意也请写邮件告诉我,如果你能把不满意的地方写在邮件上,我将感激不尽。
2018.06.22
写在云上
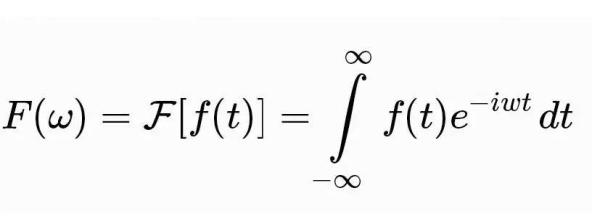







 博客主要介绍傅立叶公式的学习方法,指出其并非凭空产生,而是从低维度向量空间演变而来。先从三维空间的正交单位向量基和向量分解讲起,再过渡到希尔伯特空间,阐述其与无限维向量空间的关系,最后说明傅立叶级数在希尔伯特空间的生成,还提及傅立叶级数到傅立叶变换的跳跃待写。
博客主要介绍傅立叶公式的学习方法,指出其并非凭空产生,而是从低维度向量空间演变而来。先从三维空间的正交单位向量基和向量分解讲起,再过渡到希尔伯特空间,阐述其与无限维向量空间的关系,最后说明傅立叶级数在希尔伯特空间的生成,还提及傅立叶级数到傅立叶变换的跳跃待写。
















 1472
1472

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








