动点四边形周长最短_13道典型例题，让你彻底掌握《平行四边形综合应用之动点问题》...

【知识梳理】

(1)动点问题一般会涉及平行四边形的判定与性质定理、平行的性质、等腰三角形、等边三角形、直角三角形、梯形等知识点，应熟练运用各个知识点方能解决问题.

(2)点的运动会使它所在的线段、形状变形，因此必须寻找动点运动到哪个位置时，构成题目所需的平行四边形等图形.在探索过程中，应不断尝试，动手多画画，多找找，切勿遗漏.

(3)搞清楚题目中所提供的条件，找到适合的添加条件使得四边形为平行四边形也是解决问题的关键.

【分析】(1)表示出PB、BQ的长度，然后根据等腰三角形的两边PB＝BQ，列式进行计算即可求解；

(2)根据平行四边形的对边平行可得AD∥BC，过点Q作QE⊥AB，垂足为E，根据两直线平行，同位角相等可得∠QBE＝45°，然后求出QE的长度，再根据三角形的面积公式列式进行计算即可求解；

(3)假设能成立，列式并整理得到关于x方程，如果方程有解且在x的取值范围内，则能，否则不能．

【点评】本题考查了平行四边形的性质，等腰三角形的两边相等的性质，一元二次方程的应用，是综合性题目，难度较大，根据动点的移动表示出边PB、QB的长度是解题的关键，难度较大，计算时一定要仔细小心．

【分析】(1)由题可知，四边形AEDF为平行四边形，∠EDF＝∠A，所以在D点运动过程中，只要∠A度数不发生变化，它的度数就不变；

(2)平行四边形AEDF中，FD＝AE，AF＝ED，因为ED和AC平行，所以∠EDB和∠C相等，又在等腰三角形ABC中，∠B＝∠C，所以BE＝DE，同理，AF＝BE，即平行四边形AEDF周长等于AB的2倍20；

(3)在D点运动过程中，虽然平行四边形AEDF形状会发生变化，但是线段之间的和差关系不变，即平行四边形AEDF周长永远等于三角形ABC腰长的2倍．

【点评】本题主要考查了平行四边形中对边相等的性质及应用，以及等腰三角形的等角对等边的性质，难易程度适中．

【分析】由运动时间为x秒，则AP＝x，QC＝2x，而四边形ABQP是平行四边形，所以AP＝BQ，则得方程x＝6﹣2x求解．

【点评】本题考查了平行四边形的判定与性质．此题根据路程＝速度×时间，得出AP、QC的长，然后根据已知条件列方程求解．

【分析】(1)由题意已知，AD∥BC，要使四边形PQDC是平行四边形，则只需要让QD＝PC即可，因为Q、P点的速度

已知，AD、BC的长度已知，要求时间，用时间＝路程÷速度，即可求出时间；

(2)要使以C、D、Q、P为顶点的梯形面积等于60cm2，可以分为两种情况，点P、Q分别沿AD、BC运动或点P返回时，再利用梯形面积公式，即(QD+PC)×AB÷2＝60，因为Q、P点的速度已知，AD、AB、BC的长度已知，用t可分别表示QD、BC的长，即可求得时间t；

(3)使△PQD是等腰三角形，可分三种情况，即PQ＝PD、PQ＝QD、QD＝PD；可利用等腰三角形及直角梯形的

性质，分别用t表达等腰三角形的两腰长，再利用两腰相等即可求得时间t．

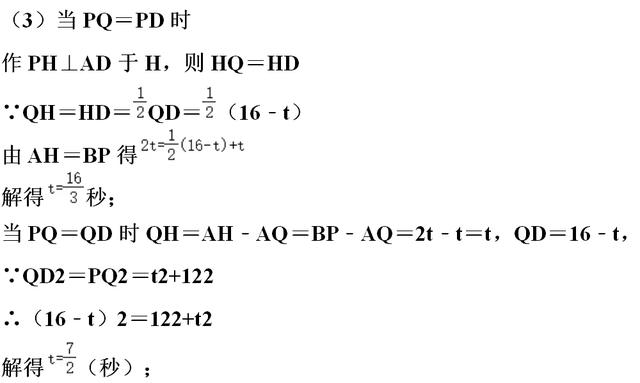
【点评】本题主要考查了直角梯形的性质、平行四边形的性质、梯形的面积、等腰三角形的性质，特别应该注意要全面考虑各种情况，不要遗漏．

【分析】设当P，Q同时出发，t秒后其中一个四边形为平行四边形，则AP＝3tcm，DP＝(24﹣3t)cm，CQ＝2tcm，BQ＝(30﹣2t)cm，分为两种情况：①当ABQP是平行四边形时，根据AP＝BQ得出方程，求出方程的解即可；②当CDPQ是平行四边形时，根据DP＝CQ得出方程，求出方程的解即可．

【点评】本题考查了平行四边形的性质的应用，能正确运用平行四边形的性质得出方程是解此题的关键，用了分类思想和方程思想，难度适中．

【分析】由题意可得当点F在C的右侧时去分析，由当AE＝CF时，以A、C、E、F为顶点四边形是平行四边形，可得方程，解方程即可求得答案．

【点评】此题考查了平行四边形的判定．此题难度适中，注意掌握数形结合思想与方程思想的应用．

【分析】首先设经过t秒，根据平行四边形的判定可得当DP＝BQ时，以点P、D、Q、B为顶点组成平行四边形，然后分情况讨论，再列出方程，求出方程的解即可．

【点评】此题考查了平行四边形的判定．此题难度适中，注意掌握数形结合思想与方程思想的应用．

【分析】(1)根据待定系数法，可得函数解析式；

(2)根据三角形的面积公式，可得方程，根据解一元一次方程，可得答案；

(3)根据两组对边分别相等的四边形是平行四边形，可得答案．

【点评】本题考查了一次函数的综合题，利用了待定系数法求函数解析式，三角形的面积公式，平行四边形的判定．

【分析】(1)由A、B的坐标利用待定系数法可求得直线AB的函数表达式；

(2)分AB为边和AB为对角线两种情况，当AB为边时，则CD∥AB且CD＝AB，过C作y轴的平行线，过D作x轴的平行线，两线交于点E，则可证明△AOB≌△CED，可求得CE、DE的长，则可求得D点坐标；当AB为对角线时，设AB的中点为F，可求得F的坐标，则F也为CD的中点，则可求得D点坐标；

(3)可设出点Q坐标为(0，t)，分AC为边和AC为对角线两种情况，当AC为边时，过点C作CM⊥y轴于点M，过点P作PN⊥y轴于点N，则可证明△ACM≌△PQN，则可求得PN、QN的长，可求得Q点的坐标；当AC为对角线时，设AC的中点为H，可求得H点的坐标，则H也为PQ的中点，则可用t表示出P点坐标，代入直线AB的解析式，可求得t的值，则可求得Q点坐标．

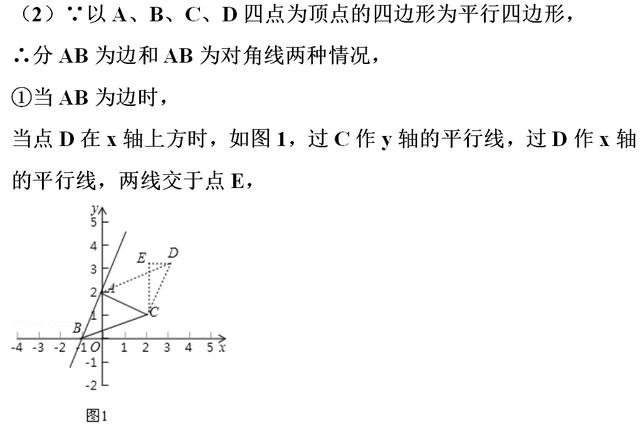
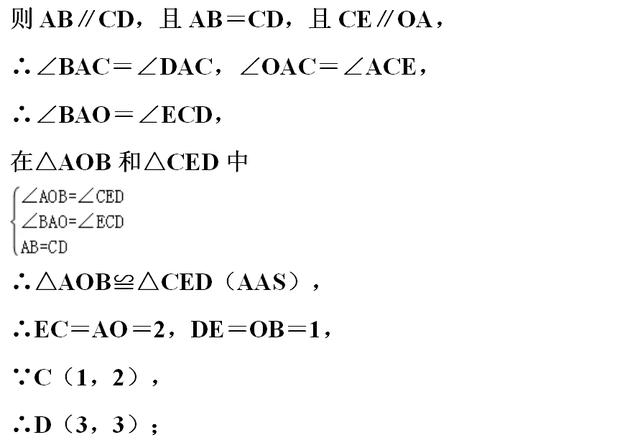
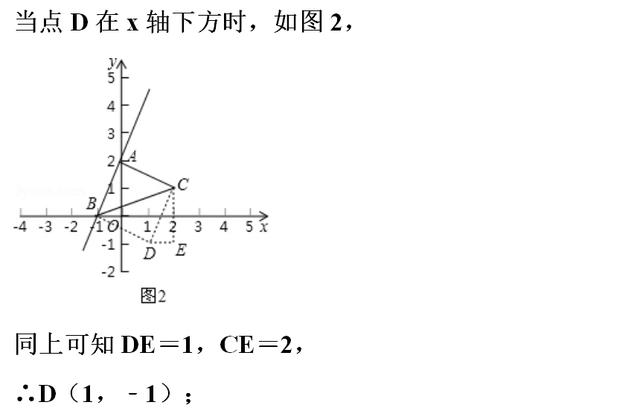
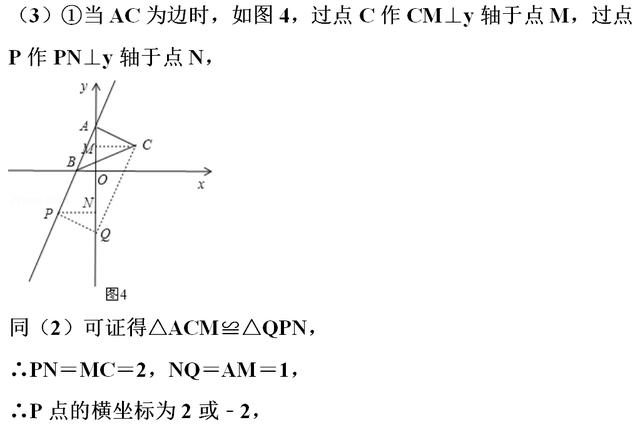
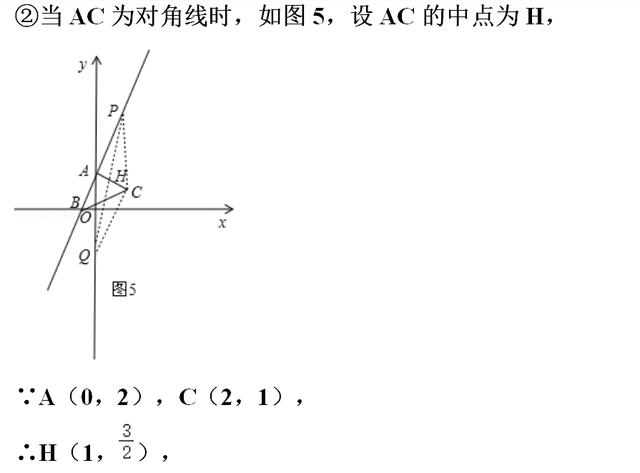
【点评】本题为一次函数的综合应用，涉及待定系数法、全等三角形的判定和性质、中点坐标公式、平行四边形的性质及分类讨论思想等知识．在(1)中注意待定系数法的应用，在(2)(3)中确定出所求点的位置是解题的关键，注意分类讨论．本题考查知识点较多，综合性较强，难度较大．

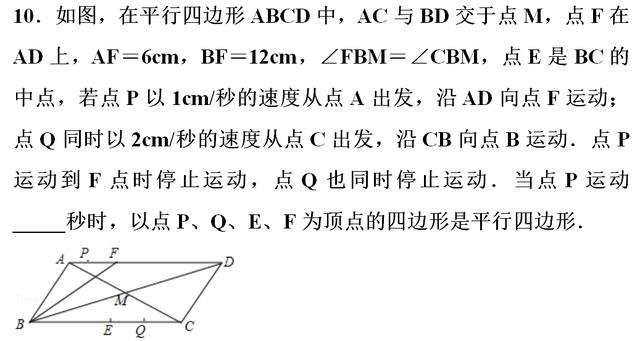
【分析】由四边形ABCD是平行四边形得出：AD∥BC，AD＝BC，∠ADB＝∠CBD，证得FB＝FD，求出AD的长，得出CE的长，设当点P运动t秒时，点P、Q、E、F为顶点的四边形是平行四边形，根据题意列出方程并解方程即可得出结果．

【点评】本题考查了平行四边形的判定与性质、等腰三角形的判定与性质、一元一次方程的应用等知识，熟练掌握平行四边形的判定与性质是解决问题的关键．

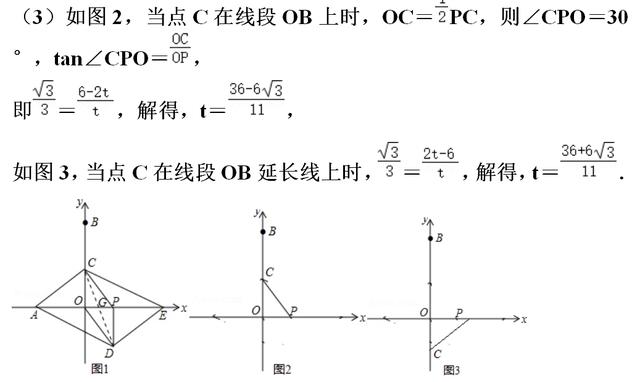
【点评】本题考查的是坐标和图形、平行四边形的判定和性质、二次函数解析式的求法、锐角三角函数知识的综合运用，正确运用分情况讨论思想和数形结合思想是解题的关键．

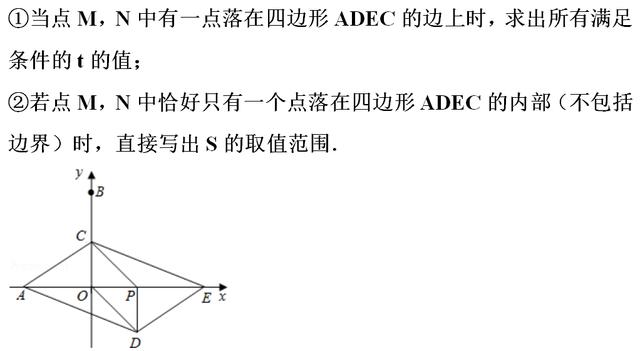
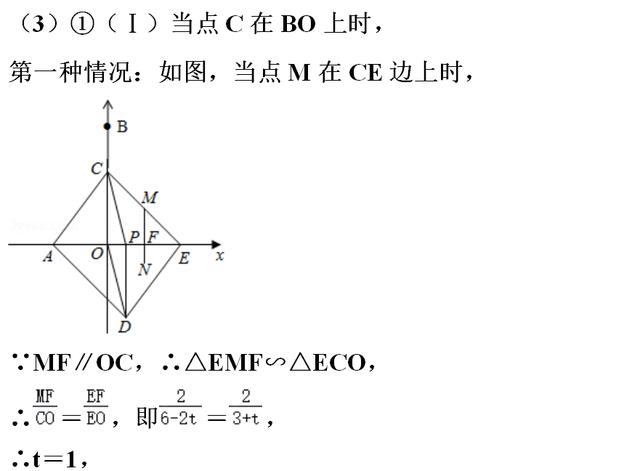
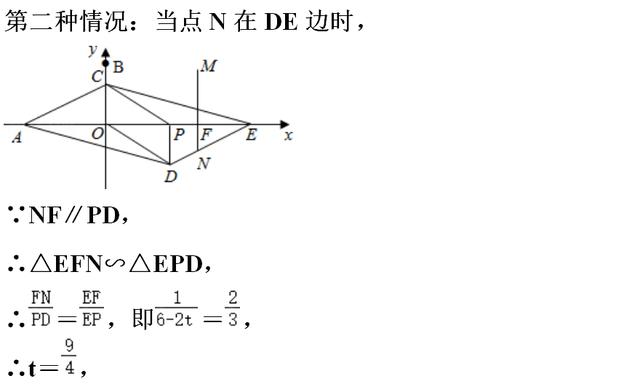
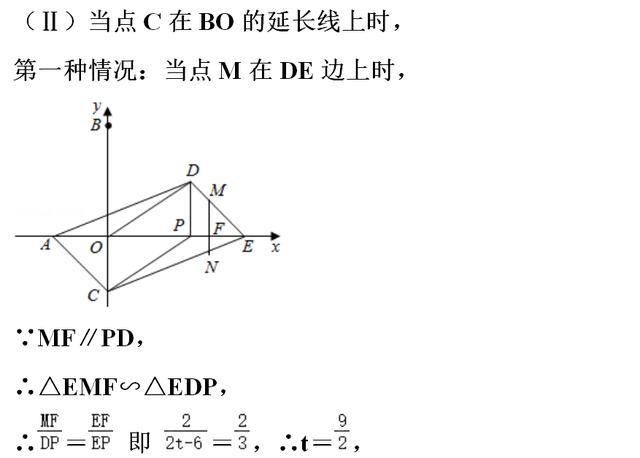
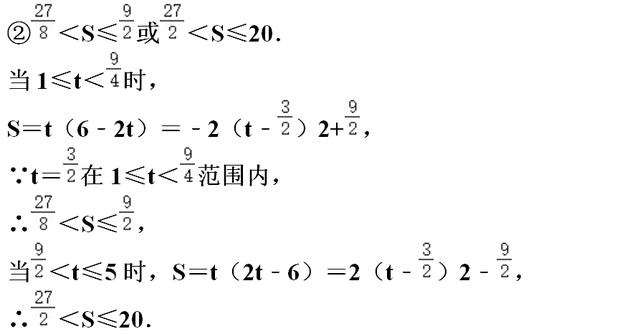
【点评】本题主要是考查了四边形的综合题，解题的关键是正确分几种不同种情况求解．

【分析】(1)当C运动到OB的中点时，根据时间t＝路程/速度即可求得，进而求得E的坐标；

(2)证明△AOC≌△EPD，则AC＝DE，∠CAO＝∠DEP，则AC和DE平行且相等，则四边形ADEC为平行四边形；

(3)首先确定直线DE，EC的解析式，分两种情形分别构建方程解决问题即可．

【点评】本题属于四边形综合题，考查了平行四边形的判定与待定系数法求函数解析式，正确求得CE和DE的解析式是关键，学会用分类讨论的思想思考问题，属于中考压轴题．

私信，发送文字“初中数学”，可以获得电子版资料哦。