1.已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
 【解答】解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP=
【解答】解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP= =
= =3,则P的坐标是(3,4).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM=
=3,则P的坐标是(3,4).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM= =3,
当P在M的左边时,CP=5﹣3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
=3,
当P在M的左边时,CP=5﹣3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
 2.如图,在直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14cm,A(16,0),C(0,2)、若点P、Q分别从C、A同时出发,点P以2cm/s速度由C向B运动,点Q以4cm/s速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为ts(0≤t≤4).
(1)求当t为多少时,四边形PQAB为平行四边形;
(2)求当t为多少时,直线PQ将梯形OABC分成左右两部分的面积比为1:2,并求出此时直线PQ的解析式.
2.如图,在直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14cm,A(16,0),C(0,2)、若点P、Q分别从C、A同时出发,点P以2cm/s速度由C向B运动,点Q以4cm/s速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为ts(0≤t≤4).
(1)求当t为多少时,四边形PQAB为平行四边形;
(2)求当t为多少时,直线PQ将梯形OABC分成左右两部分的面积比为1:2,并求出此时直线PQ的解析式.
 【解答】解:(1)t秒后,BP=(14﹣2t),AQ=4t
若四边形PQAB为平行四边形,则BP=AQ,
即14﹣2t=4t,
解得:t=
【解答】解:(1)t秒后,BP=(14﹣2t),AQ=4t
若四边形PQAB为平行四边形,则BP=AQ,
即14﹣2t=4t,
解得:t= .(4分)
(2)∵C(0,2),A(16,0)
∴OC=2,OA=16
∴S梯形OABC=
.(4分)
(2)∵C(0,2),A(16,0)
∴OC=2,OA=16
∴S梯形OABC= •
• (cm2)
∵t秒后PC=2t,OQ=16﹣4t,
∴S四边形PQOC=
(cm2)
∵t秒后PC=2t,OQ=16﹣4t,
∴S四边形PQOC= (2t+16﹣4t)×2=16﹣2t,
∵PQ将梯形OABC分成左右两部分面积比为1:2
∴S四边形PQOC=
(2t+16﹣4t)×2=16﹣2t,
∵PQ将梯形OABC分成左右两部分面积比为1:2
∴S四边形PQOC= S四边形OABC=10,
∴16﹣2t=10,∴t=3(秒).(7分)
∴t=3秒时,直线PQ将梯形OABC分成左右面积比为1:2两部分,
此时PC=6,OQ=4
∴Q(4,0)、P(6,2)
设直线PQ解析式为y=kx+b,
∴
S四边形OABC=10,
∴16﹣2t=10,∴t=3(秒).(7分)
∴t=3秒时,直线PQ将梯形OABC分成左右面积比为1:2两部分,
此时PC=6,OQ=4
∴Q(4,0)、P(6,2)
设直线PQ解析式为y=kx+b,
∴ ∴
∴ ∴直线PQ解析式为y=x﹣4.(10分)
3.如图,矩形ABCO中,B的坐标为(4
∴直线PQ解析式为y=x﹣4.(10分)
3.如图,矩形ABCO中,B的坐标为(4 ,4),一动点P从O出发,以每秒1个单位的速度,从点O出发沿OA向终点A运动,过点P作直线PF⊥OB,交OB于点F;同时将直线PF以每秒
,4),一动点P从O出发,以每秒1个单位的速度,从点O出发沿OA向终点A运动,过点P作直线PF⊥OB,交OB于点F;同时将直线PF以每秒 个单位向右平移,分别交AB、OB于点E、Q,连接PE,设运动时间为t秒,求t为何值时,PE∥OB.
个单位向右平移,分别交AB、OB于点E、Q,连接PE,设运动时间为t秒,求t为何值时,PE∥OB.
 【解答】解:∵四边形ABCO为矩形,
∴∠AOC=∠OCB=90°,
∵B的坐标为(4
【解答】解:∵四边形ABCO为矩形,
∴∠AOC=∠OCB=90°,
∵B的坐标为(4 ,4),
∴OC=4
,4),
∴OC=4 ,BC=AO=4,
由勾股定理得:OB=8,
∴∠BOC=30°,
过G作GN⊥EH于N,
由题意得:OP=t,GH=
,BC=AO=4,
由勾股定理得:OB=8,
∴∠BOC=30°,
过G作GN⊥EH于N,
由题意得:OP=t,GH= t,
∵PF∥EH,PF⊥OB,
∴EH⊥OB,
∵PE∥OB∥GN,
∴∠NGC=∠BOC=30°,
Rt△GNC中,HN=t,GN=
t,
∵PF∥EH,PF⊥OB,
∴EH⊥OB,
∵PE∥OB∥GN,
∴∠NGC=∠BOC=30°,
Rt△GNC中,HN=t,GN= t,
∴PE=GN=
t,
∴PE=GN= t,
Rt△POF中,∵∠POF=90°﹣30°=60°,
∴∠OPF=30°,
∵∠FPE=90°,
∴∠APE=60°,
∴∠AEP=30°,
∴AP=
t,
Rt△POF中,∵∠POF=90°﹣30°=60°,
∴∠OPF=30°,
∵∠FPE=90°,
∴∠APE=60°,
∴∠AEP=30°,
∴AP= PE=
PE= t,
∵OP=t,
则
t,
∵OP=t,
则 t+t=4,
t=
t+t=4,
t= ,
∴t为
,
∴t为 秒时,PE∥OB.
秒时,PE∥OB.
 4.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止、设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到 .
4.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止、设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到 .
 【解答】解:当R在PN上运动时,△MNR的面积不断增大;
当R在QP上运动时,MN一定,高为PN不变,此时面积不变;
当R在QM上运动时,面积不断减小.
∴当x=9时,点R应运动到高不变的结束,即点Q处.
所以当t=2或16﹣2=14时,四边形DEBF是矩形.
5.如图1,正方形ABCD的边长为2厘米,点E从点A开始沿AB边移动到点B,点F从点B开始沿BC边移动到点C,点G从点C开始沿CD边移动到点D,点H从点D开始沿DA边移动到点A、它们同时开始移动,且速度均为0.5厘米/秒.设运动的时间为t(秒)
(1)求证:△HAE≌△EBF;
(2)设四边形EFGH的面积为S(平方厘米),求S与t之间的函数关系式,并写出自变量t的取值范围;
(3)在图2中用描点法画出(2)中函数的图象,并观察图象,答出t为何值时,四边形EFGH的面积最小?最小值是多少?
【解答】解:当R在PN上运动时,△MNR的面积不断增大;
当R在QP上运动时,MN一定,高为PN不变,此时面积不变;
当R在QM上运动时,面积不断减小.
∴当x=9时,点R应运动到高不变的结束,即点Q处.
所以当t=2或16﹣2=14时,四边形DEBF是矩形.
5.如图1,正方形ABCD的边长为2厘米,点E从点A开始沿AB边移动到点B,点F从点B开始沿BC边移动到点C,点G从点C开始沿CD边移动到点D,点H从点D开始沿DA边移动到点A、它们同时开始移动,且速度均为0.5厘米/秒.设运动的时间为t(秒)
(1)求证:△HAE≌△EBF;
(2)设四边形EFGH的面积为S(平方厘米),求S与t之间的函数关系式,并写出自变量t的取值范围;
(3)在图2中用描点法画出(2)中函数的图象,并观察图象,答出t为何值时,四边形EFGH的面积最小?最小值是多少?

 【解答】解:(1)t秒时,AE=0.5t,BF=0.5t,DH=0.5t
∴AE=BF=DH(1分)
∵四边形ABCD为正方形
∴∠A=∠B=90°,AD=AB
∴AH=BE=2﹣0.5t(3分)
∴△HAE≌△EBF(4分)
(2)由(1)同理可得Rt△HAE≌Rt△EBF≌Rt△FCG≌Rt△GDH(5分)
【解答】解:(1)t秒时,AE=0.5t,BF=0.5t,DH=0.5t
∴AE=BF=DH(1分)
∵四边形ABCD为正方形
∴∠A=∠B=90°,AD=AB
∴AH=BE=2﹣0.5t(3分)
∴△HAE≌△EBF(4分)
(2)由(1)同理可得Rt△HAE≌Rt△EBF≌Rt△FCG≌Rt△GDH(5分)
 (7分)
=
(7分)
= (8分)
自变量t的取值范围是O≤t≤4(9分)
(3)
(8分)
自变量t的取值范围是O≤t≤4(9分)
(3) ∴图象的开口向上,对称轴为t=2,顶点坐标为(2,2)
∴图象的开口向上,对称轴为t=2,顶点坐标为(2,2)
说明:正确描点画图,图象如右图所示得(3分)(不能按自变量取值范围作图扣1分) 答:由图象可知t=2(秒)时,S最小值=2(平方厘米).(14分)
6.如图,已知正方形ABCD与正方形EFGH的边长分别是
答:由图象可知t=2(秒)时,S最小值=2(平方厘米).(14分)
6.如图,已知正方形ABCD与正方形EFGH的边长分别是 和
和 ,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7﹣2
,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7﹣2 ,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
(1)在开始运动前,O1O2= ;
(2)当两个正方形按照各自的运动方式同时运动3秒时,正方形ABCD停止旋转,这时AE= ,O1O2= ;
(3)当正方形ABCD停止旋转后,正方形EFGH继续向左平移的时间为x秒,两正方形重叠部分的面积为y,求y与x之间的函数表达式.
,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
(1)在开始运动前,O1O2= ;
(2)当两个正方形按照各自的运动方式同时运动3秒时,正方形ABCD停止旋转,这时AE= ,O1O2= ;
(3)当正方形ABCD停止旋转后,正方形EFGH继续向左平移的时间为x秒,两正方形重叠部分的面积为y,求y与x之间的函数表达式.
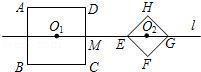 【解答】解:(1)9.
(2)0,6
【解答】解:(1)9.
(2)0,6
 (3)当正方形ABCD停止运动后,正方形EFGH继续向左平移时,与正方形ABCD重叠部分的形状也是正方形.
重叠部分的面积y与x之间的函数关系应分四种情况:
①如图1,当0≤x<4时,
∵EA=x,
∴y与x之间的函数关系式为y=
(3)当正方形ABCD停止运动后,正方形EFGH继续向左平移时,与正方形ABCD重叠部分的形状也是正方形.
重叠部分的面积y与x之间的函数关系应分四种情况:
①如图1,当0≤x<4时,
∵EA=x,
∴y与x之间的函数关系式为y= .
②如图2,当4≤x<8时,y与x之间的函数关系式为y=(2
.
②如图2,当4≤x<8时,y与x之间的函数关系式为y=(2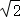 )2=8.
③如图3,当8≤x<12时,
∵CG=12﹣x,
∴y与x之间的函数关系式为y=
)2=8.
③如图3,当8≤x<12时,
∵CG=12﹣x,
∴y与x之间的函数关系式为y= =
= x2﹣12x+72.
④当x≥12时,y与x之间的函数关系式为y=0.
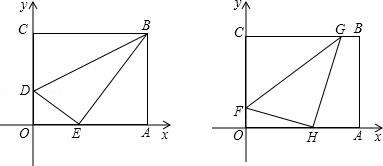
7.将一矩形纸片OABC放在平面直角坐标系中,O为顶点,点A在x轴上,点C在y轴上,OA=10,OC=8.
(1)如右上图,在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作点E.
①求点E的坐标及折痕BD的长;
②在x轴上取两点M,N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M和点N的坐标;
(2)如右下图,在OC,BC边上分别取点F,G,将△GCF沿GF折叠,使点C恰好落在OA边上,记作点H.设OH=x,四边形OHGC的面积为S,求S与x之间的函数关系式,并写出自变量x的取值范围.
x2﹣12x+72.
④当x≥12时,y与x之间的函数关系式为y=0.
7.将一矩形纸片OABC放在平面直角坐标系中,O为顶点,点A在x轴上,点C在y轴上,OA=10,OC=8.
(1)如右上图,在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作点E.
①求点E的坐标及折痕BD的长;
②在x轴上取两点M,N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M和点N的坐标;
(2)如右下图,在OC,BC边上分别取点F,G,将△GCF沿GF折叠,使点C恰好落在OA边上,记作点H.设OH=x,四边形OHGC的面积为S,求S与x之间的函数关系式,并写出自变量x的取值范围.
 【解答】解:(1)①∵四边形OABC为矩形,
∴BC=OA=10,AB=OC=8,
∵△BCD沿BD折叠,使点C恰好落在OA边E点上,
∴BC=BE=10,DC=DE,
在Rt△ABE中,BE=10,AB=8,
∴AE=6,
∴OE=10﹣6=4,
∴E点坐标为(4,0);
在Rt△ODE中,设DE=x,则OD=OC﹣DC=OC﹣DE=8﹣x,
∴x2=42+(8﹣x)2,解得x=5,
在Rt△BDE中,
BD=
【解答】解:(1)①∵四边形OABC为矩形,
∴BC=OA=10,AB=OC=8,
∵△BCD沿BD折叠,使点C恰好落在OA边E点上,
∴BC=BE=10,DC=DE,
在Rt△ABE中,BE=10,AB=8,
∴AE=6,
∴OE=10﹣6=4,
∴E点坐标为(4,0);
在Rt△ODE中,设DE=x,则OD=OC﹣DC=OC﹣DE=8﹣x,
∴x2=42+(8﹣x)2,解得x=5,
在Rt△BDE中,
BD= =5
=5 ;
②以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,如图:
∴B′的坐标为(10,﹣8),DD′=MN=4.5,
∴D′的坐标为(4.5,3),
设直线D′B′的解析式为y=kx+b,
把B′(10,﹣8),D′(4.5,3)代入得
10k+b=﹣8,4.5k+b=3,
解得k=﹣2,b=12,
∴直线D′B′的解析式为y=﹣2x+12,
令y=0,得﹣2x+12=0,解得x=6,
∴M(1.5,0);N(6,0).
(2)过点H作HM⊥BC于M,则MG=HG﹣x,
∵△GCF沿GF折叠得到△GHF,
∴HG=CG,故MG可表示为CG﹣x,
在Rt△HMG中,HG2=MG2+MH2,即HG2=(CG﹣x)2+64,
解得:CG=
;
②以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,如图:
∴B′的坐标为(10,﹣8),DD′=MN=4.5,
∴D′的坐标为(4.5,3),
设直线D′B′的解析式为y=kx+b,
把B′(10,﹣8),D′(4.5,3)代入得
10k+b=﹣8,4.5k+b=3,
解得k=﹣2,b=12,
∴直线D′B′的解析式为y=﹣2x+12,
令y=0,得﹣2x+12=0,解得x=6,
∴M(1.5,0);N(6,0).
(2)过点H作HM⊥BC于M,则MG=HG﹣x,
∵△GCF沿GF折叠得到△GHF,
∴HG=CG,故MG可表示为CG﹣x,
在Rt△HMG中,HG2=MG2+MH2,即HG2=(CG﹣x)2+64,
解得:CG= ,
∴SOHGC=
,
∴SOHGC= (CG+OH)•OC=
(CG+OH)•OC= ,即y=
,即y= ,
点F与点O重合点G与点B重合、点F与点O重合分别是点F的两个极限,
1、点G与点B重合时,由①的结论可得,此时OH=4,
2、点F与点O重合时,OH=8,
综上可得:y=
,
点F与点O重合点G与点B重合、点F与点O重合分别是点F的两个极限,
1、点G与点B重合时,由①的结论可得,此时OH=4,
2、点F与点O重合时,OH=8,
综上可得:y= ,(4≤x≤8).
,(4≤x≤8).
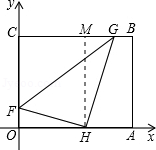
 8.如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形ADMN的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是( )
8.如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形ADMN的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是( )
 A.
A. B.
B. C.
C. D.
D. 【解答】解:因为在直角梯形ABCD中,DC∥AB,∠A=90°,
所以四边形ANMD也是直角梯形,因此它的面积为
【解答】解:因为在直角梯形ABCD中,DC∥AB,∠A=90°,
所以四边形ANMD也是直角梯形,因此它的面积为 (DM+AN)×AD,因为DM=t,AN=28﹣2t,AD=4;
所以四边形AMND的面积y=
(DM+AN)×AD,因为DM=t,AN=28﹣2t,AD=4;
所以四边形AMND的面积y= (t+28﹣2t)×4=﹣2t+56.
因为当其中一个动点到达端点停止运动时,另一个动点也随之停止运动;
所以当N点到达A点时,2t=28,t=14;
所以自变量t的取值范围是0<t<14.
故选:D.
9.如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=
(t+28﹣2t)×4=﹣2t+56.
因为当其中一个动点到达端点停止运动时,另一个动点也随之停止运动;
所以当N点到达A点时,2t=28,t=14;
所以自变量t的取值范围是0<t<14.
故选:D.
9.如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD= ,∠C=45°,点P是BC边上一动点,设PB的长为x.
(1)当x的值为 时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为 时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
,∠C=45°,点P是BC边上一动点,设PB的长为x.
(1)当x的值为 时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为 时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
 【解答】解:(1)如图,分别过A、D作AM⊥BC于M,DN⊥CB于N,
则四边形AMND是矩形,
∴AM=DN,AD=MN=5,
而CD=
【解答】解:(1)如图,分别过A、D作AM⊥BC于M,DN⊥CB于N,
则四边形AMND是矩形,
∴AM=DN,AD=MN=5,
而CD= ,∠C=45°,
∴DN=CN=CD•sin∠C=4
,∠C=45°,
∴DN=CN=CD•sin∠C=4 ×
× =4=AM,
∴BM=CB﹣CN﹣MN=3,
若点P、A、D、E为顶点的四边形为直角梯形,
则∠APC=90°或∠DEB=90°,
当∠APC=90°时,
∴P与M重合,
∴BP=BM=3;
当∠DPB=90°时,P与N重合,
∴BP=BN=8;
故当x的值为3或8时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)若以点P、A、D、E为顶点的四边形为平行四边形,那么AD=PE,
有两种情况:①当P在E的左边,
∵E是BC的中点,
∴BE=6,
∴BP=BE﹣PE=6﹣5=1;
②当P在E的右边,
BP=BE+PE=6+5=11;
故当x的值为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)由(2)知,①当BP=1时,此时CN=DN=4,NE=6﹣4=2,
∴DE=
=4=AM,
∴BM=CB﹣CN﹣MN=3,
若点P、A、D、E为顶点的四边形为直角梯形,
则∠APC=90°或∠DEB=90°,
当∠APC=90°时,
∴P与M重合,
∴BP=BM=3;
当∠DPB=90°时,P与N重合,
∴BP=BN=8;
故当x的值为3或8时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)若以点P、A、D、E为顶点的四边形为平行四边形,那么AD=PE,
有两种情况:①当P在E的左边,
∵E是BC的中点,
∴BE=6,
∴BP=BE﹣PE=6﹣5=1;
②当P在E的右边,
BP=BE+PE=6+5=11;
故当x的值为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)由(2)知,①当BP=1时,此时CN=DN=4,NE=6﹣4=2,
∴DE= =
= =2
=2 ≠AD,故不能构成菱形.
②当BP′=11时,以点P′、A、D、E为顶点的四边形是平行四边形
∴EP′=AD=5,
过D作DN⊥BC于N,
∵CD=
≠AD,故不能构成菱形.
②当BP′=11时,以点P′、A、D、E为顶点的四边形是平行四边形
∴EP′=AD=5,
过D作DN⊥BC于N,
∵CD= ,∠C=45°,
则DN=CN=4,
∴NP′=BP′﹣BN=BP′﹣(BC﹣CN)=11﹣12+4=3.
∴DP′=
,∠C=45°,
则DN=CN=4,
∴NP′=BP′﹣BN=BP′﹣(BC﹣CN)=11﹣12+4=3.
∴DP′= =
=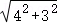 =5,
∴EP′=DP′,
故此时▱P′DAE是菱形.
即以点P、A、D、E为顶点的四边形能构成菱形;
=5,
∴EP′=DP′,
故此时▱P′DAE是菱形.
即以点P、A、D、E为顶点的四边形能构成菱形;

 10.已知:等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点,线段MN运动的时间为t秒.
(1)线段MN在运动的过程中,t为何值时,四边形MNQP恰为矩形并求出该矩形的面积;
(2)线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t,求四边形MNQP的面积S随运动时间t变化的函数关系式,并写出自变量t的取值范围.
10.已知:等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点,线段MN运动的时间为t秒.
(1)线段MN在运动的过程中,t为何值时,四边形MNQP恰为矩形并求出该矩形的面积;
(2)线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t,求四边形MNQP的面积S随运动时间t变化的函数关系式,并写出自变量t的取值范围.
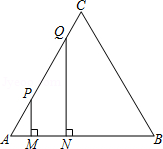 【解答】解:(1)过点C作CD⊥AB,垂足为D,则AD=2,
当MN运动到被CD垂直平分时,四边形MNQP是矩形,
即当AM=
【解答】解:(1)过点C作CD⊥AB,垂足为D,则AD=2,
当MN运动到被CD垂直平分时,四边形MNQP是矩形,
即当AM= 时,四边形MNQP是矩形,
∴t=
时,四边形MNQP是矩形,
∴t= 秒时,四边形MNQP是矩形,
∵PM=AMtan60°=
秒时,四边形MNQP是矩形,
∵PM=AMtan60°=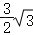 ,
PQ=MN=AB﹣2AM=4﹣3=1,
∴S四边形MNQP=PM•PQ=
,
PQ=MN=AB﹣2AM=4﹣3=1,
∴S四边形MNQP=PM•PQ=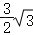 ;
(2)①当0<t≤1时,点P、Q都在AC上,并且四边形PMNQ为直角梯形,
在Rt△AMP中,
∵∠A=60°,AM=t,tan∠A=
;
(2)①当0<t≤1时,点P、Q都在AC上,并且四边形PMNQ为直角梯形,
在Rt△AMP中,
∵∠A=60°,AM=t,tan∠A=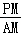 ,
∴PM=tan60°×AM=
,
∴PM=tan60°×AM= AM=
AM= t,
在Rt△ANQ中,
而AN=AM+MN=t+1,
∴QN=
t,
在Rt△ANQ中,
而AN=AM+MN=t+1,
∴QN= AN=
AN= (t+1),
∴S四边形MNQP=
(t+1),
∴S四边形MNQP= (PM+QN)MN=
(PM+QN)MN= [
[ t+
t+ (t+1)]=
(t+1)]= t+
t+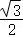 ;
②当1<t<2时,
点P在AC上,点Q在BC上,
PM=
;
②当1<t<2时,
点P在AC上,点Q在BC上,
PM= t,
BN=AB﹣AM﹣MN=4﹣1﹣t=3﹣t,
在Rt△BNQ中,
QN=
t,
BN=AB﹣AM﹣MN=4﹣1﹣t=3﹣t,
在Rt△BNQ中,
QN= BN=
BN= (3﹣t),
∴S四边形MNQP=
(3﹣t),
∴S四边形MNQP= (PM+QN)MN=
(PM+QN)MN= [
[ t+
t+ (3﹣t)]×1=
(3﹣t)]×1=
 ;
③当2≤t<3时,点P、Q都在BC上,
BM=4﹣t,BN=3﹣t,
∴PM=
;
③当2≤t<3时,点P、Q都在BC上,
BM=4﹣t,BN=3﹣t,
∴PM= BM=
BM= (4﹣t),QN=
(4﹣t),QN= BN=
BN= (3﹣t),
∴S四边形MNQP=
(3﹣t),
∴S四边形MNQP= (PM+QN)MN=
(PM+QN)MN= [
[ (3﹣t)+
(3﹣t)+ (4﹣t)]=
(4﹣t)]= ﹣
﹣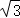 t.
综上所述:当0<t≤1时,S四边形MNQP=
t.
综上所述:当0<t≤1时,S四边形MNQP=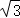 t+
t+ ;当1<t<2时,S四边形MNQP=
;当1<t<2时,S四边形MNQP=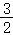
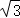 ;
当2≤t<3时,S四边形MNQP=
;
当2≤t<3时,S四边形MNQP= ﹣
﹣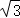 t. (10分)
t. (10分)


 11.如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A﹣B﹣C﹣D的路线作匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(秒).
①当t=5时,求出点P的坐标;
②若△OAP的面积为s,试求出s与t之间的函数关系式(并写出相应的自变量t的取值范围).
11.如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A﹣B﹣C﹣D的路线作匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(秒).
①当t=5时,求出点P的坐标;
②若△OAP的面积为s,试求出s与t之间的函数关系式(并写出相应的自变量t的取值范围).
 【解答】解:(1)P点从A点运动到D点所需的时间=(3+5+3)÷1=11(秒)
(2)①当t=5时,P点从A点运动到BC上,
过点P作PE⊥AD于点E.
此时A点到E点的距离=10,AB+BP=5,
∴BP=2
则PE=AB=3,AE=BP=2
∴OE=OA+AE=10+2=12
∴点P的坐标为(12,3).
②分三种情况:
i.0<t≤3时,点P在AB上运动,此时OA=2t,AP=t
∴s=
【解答】解:(1)P点从A点运动到D点所需的时间=(3+5+3)÷1=11(秒)
(2)①当t=5时,P点从A点运动到BC上,
过点P作PE⊥AD于点E.
此时A点到E点的距离=10,AB+BP=5,
∴BP=2
则PE=AB=3,AE=BP=2
∴OE=OA+AE=10+2=12
∴点P的坐标为(12,3).
②分三种情况:
i.0<t≤3时,点P在AB上运动,此时OA=2t,AP=t
∴s=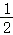 ×2t×t=t2
ii.3<t≤8时,点P在BC上运动,此时OA=2t
∴s=
×2t×t=t2
ii.3<t≤8时,点P在BC上运动,此时OA=2t
∴s=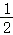 ×2t×3=3t
iii.8<t<11时,点P在CD上运动,此时OA=2t,AB+BC+CP=t
∴DP=(AB+BC+CD)﹣(AB+BC+CP)=11﹣t
∴s=
×2t×3=3t
iii.8<t<11时,点P在CD上运动,此时OA=2t,AB+BC+CP=t
∴DP=(AB+BC+CD)﹣(AB+BC+CP)=11﹣t
∴s=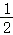 ×2t×(11﹣t)=﹣t2+11t
综上所述,s与t之间的函数关系式是:
当0<t≤3时,s=t2;
当3<t≤8时,s=3t;
当8<t<11时,s=﹣t2+11t.
×2t×(11﹣t)=﹣t2+11t
综上所述,s与t之间的函数关系式是:
当0<t≤3时,s=t2;
当3<t≤8时,s=3t;
当8<t<11时,s=﹣t2+11t.
 12.如图,在矩形OABC中,已知A,C两点的坐标分别为A(4,0),C(0,2),D为OA的中点.设点P是∠AOC平分线上的一个动点(不与点O重合).
(1)试证明:无论点P运动到何处,PC总与PD相等;
(2)当点P运动到与点B的距离最小时,求P的坐标;
(3)已知E(1,﹣1),当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长.
12.如图,在矩形OABC中,已知A,C两点的坐标分别为A(4,0),C(0,2),D为OA的中点.设点P是∠AOC平分线上的一个动点(不与点O重合).
(1)试证明:无论点P运动到何处,PC总与PD相等;
(2)当点P运动到与点B的距离最小时,求P的坐标;
(3)已知E(1,﹣1),当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长.
 【解答】(1)证明:∵A(4,0),C(0,2),D为OA的中点,
∴D点坐标为(2,0),
∴OC=OD,
又∵点P是∠AOC平分线上的一个动点(不与点O重合),
∴∠COP=∠DOP=45°,
∴△POC≌△POD,
∴PC=PD,
即无论点P运动到何处,PC总与PD相等;
(2)解:过B作BP垂直∠AOC的平分线于P点,过P点作PN⊥x轴于N,交BC于M点,OP交BC于H点,如图,
∵OP平分∠AOC,
∴∠COP=∠NOP=45°,
∴△PHM、△COH和△PON都是等腰直角三角形,
∴△PHB是等腰直角三角形,
∴PM垂直平分BH,
∴CH=CO=2,
∴BH=4﹣2=2,
∴PM=
【解答】(1)证明:∵A(4,0),C(0,2),D为OA的中点,
∴D点坐标为(2,0),
∴OC=OD,
又∵点P是∠AOC平分线上的一个动点(不与点O重合),
∴∠COP=∠DOP=45°,
∴△POC≌△POD,
∴PC=PD,
即无论点P运动到何处,PC总与PD相等;
(2)解:过B作BP垂直∠AOC的平分线于P点,过P点作PN⊥x轴于N,交BC于M点,OP交BC于H点,如图,
∵OP平分∠AOC,
∴∠COP=∠NOP=45°,
∴△PHM、△COH和△PON都是等腰直角三角形,
∴△PHB是等腰直角三角形,
∴PM垂直平分BH,
∴CH=CO=2,
∴BH=4﹣2=2,
∴PM= BH=1,
∴ON=PN=1+2=3,
∴P点坐标为(3,3);
(3)解:连CE交∠AOC的平分线于P点,连PD、CD,ED,如图,
∵OC=OD,OP平分直角AOC,
∴OP垂直平分CD,
∴PC=PD,
∴PD+PE=PC+PE=CE,
此时△PDE的周长最小,
设直线CE的解析式为y=kx+b(k≠0),
把C(0,2)、E(1,﹣1)分别代入得,b=2,k+b=﹣1,解得k=﹣3,b=2,
∴直线CE的解析式为y=﹣3x+2,
而P点的横纵坐标相等,设P(a,a),把P点坐标代入y=﹣3x+2得,a=﹣3a+2,解得a=
BH=1,
∴ON=PN=1+2=3,
∴P点坐标为(3,3);
(3)解:连CE交∠AOC的平分线于P点,连PD、CD,ED,如图,
∵OC=OD,OP平分直角AOC,
∴OP垂直平分CD,
∴PC=PD,
∴PD+PE=PC+PE=CE,
此时△PDE的周长最小,
设直线CE的解析式为y=kx+b(k≠0),
把C(0,2)、E(1,﹣1)分别代入得,b=2,k+b=﹣1,解得k=﹣3,b=2,
∴直线CE的解析式为y=﹣3x+2,
而P点的横纵坐标相等,设P(a,a),把P点坐标代入y=﹣3x+2得,a=﹣3a+2,解得a= ,
∴P点坐标为(
,
∴P点坐标为( ,
, ),
∵CE=
),
∵CE= =
= ,DE=
,DE=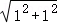 =
= ,
∴此时△PDE的周长=
,
∴此时△PDE的周长= +
+ .
.


 【解答】解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP=
【解答】解:(1)OD是等腰三角形的底边时,P就是OD的垂直平分线与CB的交点,此时OP=PD≠5;
(2)OD是等腰三角形的一条腰时:
①若点O是顶角顶点时,P点就是以点O为圆心,以5为半径的弧与CB的交点,
在直角△OPC中,CP= =
= =3,则P的坐标是(3,4).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM=
=3,则P的坐标是(3,4).
②若D是顶角顶点时,P点就是以点D为圆心,以5为半径的弧与CB的交点,
过D作DM⊥BC于点M,
在直角△PDM中,PM= =3,
当P在M的左边时,CP=5﹣3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
=3,
当P在M的左边时,CP=5﹣3=2,则P的坐标是(2,4);
当P在M的右侧时,CP=5+3=8,则P的坐标是(8,4).
故P的坐标为:(3,4)或(2,4)或(8,4).
故答案为:(3,4)或(2,4)或(8,4).
 2.如图,在直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14cm,A(16,0),C(0,2)、若点P、Q分别从C、A同时出发,点P以2cm/s速度由C向B运动,点Q以4cm/s速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为ts(0≤t≤4).
(1)求当t为多少时,四边形PQAB为平行四边形;
(2)求当t为多少时,直线PQ将梯形OABC分成左右两部分的面积比为1:2,并求出此时直线PQ的解析式.
2.如图,在直角坐标系中,四边形OABC为直角梯形,OA∥BC,BC=14cm,A(16,0),C(0,2)、若点P、Q分别从C、A同时出发,点P以2cm/s速度由C向B运动,点Q以4cm/s速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为ts(0≤t≤4).
(1)求当t为多少时,四边形PQAB为平行四边形;
(2)求当t为多少时,直线PQ将梯形OABC分成左右两部分的面积比为1:2,并求出此时直线PQ的解析式.
 【解答】解:(1)t秒后,BP=(14﹣2t),AQ=4t
若四边形PQAB为平行四边形,则BP=AQ,
即14﹣2t=4t,
解得:t=
【解答】解:(1)t秒后,BP=(14﹣2t),AQ=4t
若四边形PQAB为平行四边形,则BP=AQ,
即14﹣2t=4t,
解得:t= .(4分)
(2)∵C(0,2),A(16,0)
∴OC=2,OA=16
∴S梯形OABC=
.(4分)
(2)∵C(0,2),A(16,0)
∴OC=2,OA=16
∴S梯形OABC= •
• (cm2)
∵t秒后PC=2t,OQ=16﹣4t,
∴S四边形PQOC=
(cm2)
∵t秒后PC=2t,OQ=16﹣4t,
∴S四边形PQOC= (2t+16﹣4t)×2=16﹣2t,
∵PQ将梯形OABC分成左右两部分面积比为1:2
∴S四边形PQOC=
(2t+16﹣4t)×2=16﹣2t,
∵PQ将梯形OABC分成左右两部分面积比为1:2
∴S四边形PQOC= S四边形OABC=10,
∴16﹣2t=10,∴t=3(秒).(7分)
∴t=3秒时,直线PQ将梯形OABC分成左右面积比为1:2两部分,
此时PC=6,OQ=4
∴Q(4,0)、P(6,2)
设直线PQ解析式为y=kx+b,
∴
S四边形OABC=10,
∴16﹣2t=10,∴t=3(秒).(7分)
∴t=3秒时,直线PQ将梯形OABC分成左右面积比为1:2两部分,
此时PC=6,OQ=4
∴Q(4,0)、P(6,2)
设直线PQ解析式为y=kx+b,
∴ ∴
∴ ∴直线PQ解析式为y=x﹣4.(10分)
3.如图,矩形ABCO中,B的坐标为(4
∴直线PQ解析式为y=x﹣4.(10分)
3.如图,矩形ABCO中,B的坐标为(4 ,4),一动点P从O出发,以每秒1个单位的速度,从点O出发沿OA向终点A运动,过点P作直线PF⊥OB,交OB于点F;同时将直线PF以每秒
,4),一动点P从O出发,以每秒1个单位的速度,从点O出发沿OA向终点A运动,过点P作直线PF⊥OB,交OB于点F;同时将直线PF以每秒 个单位向右平移,分别交AB、OB于点E、Q,连接PE,设运动时间为t秒,求t为何值时,PE∥OB.
个单位向右平移,分别交AB、OB于点E、Q,连接PE,设运动时间为t秒,求t为何值时,PE∥OB.
 【解答】解:∵四边形ABCO为矩形,
∴∠AOC=∠OCB=90°,
∵B的坐标为(4
【解答】解:∵四边形ABCO为矩形,
∴∠AOC=∠OCB=90°,
∵B的坐标为(4 ,4),
∴OC=4
,4),
∴OC=4 ,BC=AO=4,
由勾股定理得:OB=8,
∴∠BOC=30°,
过G作GN⊥EH于N,
由题意得:OP=t,GH=
,BC=AO=4,
由勾股定理得:OB=8,
∴∠BOC=30°,
过G作GN⊥EH于N,
由题意得:OP=t,GH= t,
∵PF∥EH,PF⊥OB,
∴EH⊥OB,
∵PE∥OB∥GN,
∴∠NGC=∠BOC=30°,
Rt△GNC中,HN=t,GN=
t,
∵PF∥EH,PF⊥OB,
∴EH⊥OB,
∵PE∥OB∥GN,
∴∠NGC=∠BOC=30°,
Rt△GNC中,HN=t,GN= t,
∴PE=GN=
t,
∴PE=GN= t,
Rt△POF中,∵∠POF=90°﹣30°=60°,
∴∠OPF=30°,
∵∠FPE=90°,
∴∠APE=60°,
∴∠AEP=30°,
∴AP=
t,
Rt△POF中,∵∠POF=90°﹣30°=60°,
∴∠OPF=30°,
∵∠FPE=90°,
∴∠APE=60°,
∴∠AEP=30°,
∴AP= PE=
PE= t,
∵OP=t,
则
t,
∵OP=t,
则 t+t=4,
t=
t+t=4,
t= ,
∴t为
,
∴t为 秒时,PE∥OB.
秒时,PE∥OB.
 4.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止、设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到 .
4.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止、设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到 .
 【解答】解:当R在PN上运动时,△MNR的面积不断增大;
当R在QP上运动时,MN一定,高为PN不变,此时面积不变;
当R在QM上运动时,面积不断减小.
∴当x=9时,点R应运动到高不变的结束,即点Q处.
所以当t=2或16﹣2=14时,四边形DEBF是矩形.
5.如图1,正方形ABCD的边长为2厘米,点E从点A开始沿AB边移动到点B,点F从点B开始沿BC边移动到点C,点G从点C开始沿CD边移动到点D,点H从点D开始沿DA边移动到点A、它们同时开始移动,且速度均为0.5厘米/秒.设运动的时间为t(秒)
(1)求证:△HAE≌△EBF;
(2)设四边形EFGH的面积为S(平方厘米),求S与t之间的函数关系式,并写出自变量t的取值范围;
(3)在图2中用描点法画出(2)中函数的图象,并观察图象,答出t为何值时,四边形EFGH的面积最小?最小值是多少?
【解答】解:当R在PN上运动时,△MNR的面积不断增大;
当R在QP上运动时,MN一定,高为PN不变,此时面积不变;
当R在QM上运动时,面积不断减小.
∴当x=9时,点R应运动到高不变的结束,即点Q处.
所以当t=2或16﹣2=14时,四边形DEBF是矩形.
5.如图1,正方形ABCD的边长为2厘米,点E从点A开始沿AB边移动到点B,点F从点B开始沿BC边移动到点C,点G从点C开始沿CD边移动到点D,点H从点D开始沿DA边移动到点A、它们同时开始移动,且速度均为0.5厘米/秒.设运动的时间为t(秒)
(1)求证:△HAE≌△EBF;
(2)设四边形EFGH的面积为S(平方厘米),求S与t之间的函数关系式,并写出自变量t的取值范围;
(3)在图2中用描点法画出(2)中函数的图象,并观察图象,答出t为何值时,四边形EFGH的面积最小?最小值是多少?
| t | |||||
| s |

 【解答】解:(1)t秒时,AE=0.5t,BF=0.5t,DH=0.5t
∴AE=BF=DH(1分)
∵四边形ABCD为正方形
∴∠A=∠B=90°,AD=AB
∴AH=BE=2﹣0.5t(3分)
∴△HAE≌△EBF(4分)
(2)由(1)同理可得Rt△HAE≌Rt△EBF≌Rt△FCG≌Rt△GDH(5分)
【解答】解:(1)t秒时,AE=0.5t,BF=0.5t,DH=0.5t
∴AE=BF=DH(1分)
∵四边形ABCD为正方形
∴∠A=∠B=90°,AD=AB
∴AH=BE=2﹣0.5t(3分)
∴△HAE≌△EBF(4分)
(2)由(1)同理可得Rt△HAE≌Rt△EBF≌Rt△FCG≌Rt△GDH(5分)
 (7分)
=
(7分)
= (8分)
自变量t的取值范围是O≤t≤4(9分)
(3)
(8分)
自变量t的取值范围是O≤t≤4(9分)
(3) ∴图象的开口向上,对称轴为t=2,顶点坐标为(2,2)
∴图象的开口向上,对称轴为t=2,顶点坐标为(2,2)
| t | 0 | 1 | 2 | 3 | 4 |
| s | 4 | 2.5 | 2 | 2.5 | 4 |
 答:由图象可知t=2(秒)时,S最小值=2(平方厘米).(14分)
6.如图,已知正方形ABCD与正方形EFGH的边长分别是
答:由图象可知t=2(秒)时,S最小值=2(平方厘米).(14分)
6.如图,已知正方形ABCD与正方形EFGH的边长分别是 和
和 ,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7﹣2
,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7﹣2 ,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
(1)在开始运动前,O1O2= ;
(2)当两个正方形按照各自的运动方式同时运动3秒时,正方形ABCD停止旋转,这时AE= ,O1O2= ;
(3)当正方形ABCD停止旋转后,正方形EFGH继续向左平移的时间为x秒,两正方形重叠部分的面积为y,求y与x之间的函数表达式.
,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
(1)在开始运动前,O1O2= ;
(2)当两个正方形按照各自的运动方式同时运动3秒时,正方形ABCD停止旋转,这时AE= ,O1O2= ;
(3)当正方形ABCD停止旋转后,正方形EFGH继续向左平移的时间为x秒,两正方形重叠部分的面积为y,求y与x之间的函数表达式.
 【解答】解:(1)9.
(2)0,6
【解答】解:(1)9.
(2)0,6
 (3)当正方形ABCD停止运动后,正方形EFGH继续向左平移时,与正方形ABCD重叠部分的形状也是正方形.
重叠部分的面积y与x之间的函数关系应分四种情况:
①如图1,当0≤x<4时,
∵EA=x,
∴y与x之间的函数关系式为y=
(3)当正方形ABCD停止运动后,正方形EFGH继续向左平移时,与正方形ABCD重叠部分的形状也是正方形.
重叠部分的面积y与x之间的函数关系应分四种情况:
①如图1,当0≤x<4时,
∵EA=x,
∴y与x之间的函数关系式为y= .
②如图2,当4≤x<8时,y与x之间的函数关系式为y=(2
.
②如图2,当4≤x<8时,y与x之间的函数关系式为y=(2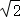 )2=8.
③如图3,当8≤x<12时,
∵CG=12﹣x,
∴y与x之间的函数关系式为y=
)2=8.
③如图3,当8≤x<12时,
∵CG=12﹣x,
∴y与x之间的函数关系式为y= =
= x2﹣12x+72.
④当x≥12时,y与x之间的函数关系式为y=0.
7.将一矩形纸片OABC放在平面直角坐标系中,O为顶点,点A在x轴上,点C在y轴上,OA=10,OC=8.
(1)如右上图,在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作点E.
①求点E的坐标及折痕BD的长;
②在x轴上取两点M,N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M和点N的坐标;
(2)如右下图,在OC,BC边上分别取点F,G,将△GCF沿GF折叠,使点C恰好落在OA边上,记作点H.设OH=x,四边形OHGC的面积为S,求S与x之间的函数关系式,并写出自变量x的取值范围.
x2﹣12x+72.
④当x≥12时,y与x之间的函数关系式为y=0.
7.将一矩形纸片OABC放在平面直角坐标系中,O为顶点,点A在x轴上,点C在y轴上,OA=10,OC=8.
(1)如右上图,在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作点E.
①求点E的坐标及折痕BD的长;
②在x轴上取两点M,N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M和点N的坐标;
(2)如右下图,在OC,BC边上分别取点F,G,将△GCF沿GF折叠,使点C恰好落在OA边上,记作点H.设OH=x,四边形OHGC的面积为S,求S与x之间的函数关系式,并写出自变量x的取值范围.
 【解答】解:(1)①∵四边形OABC为矩形,
∴BC=OA=10,AB=OC=8,
∵△BCD沿BD折叠,使点C恰好落在OA边E点上,
∴BC=BE=10,DC=DE,
在Rt△ABE中,BE=10,AB=8,
∴AE=6,
∴OE=10﹣6=4,
∴E点坐标为(4,0);
在Rt△ODE中,设DE=x,则OD=OC﹣DC=OC﹣DE=8﹣x,
∴x2=42+(8﹣x)2,解得x=5,
在Rt△BDE中,
BD=
【解答】解:(1)①∵四边形OABC为矩形,
∴BC=OA=10,AB=OC=8,
∵△BCD沿BD折叠,使点C恰好落在OA边E点上,
∴BC=BE=10,DC=DE,
在Rt△ABE中,BE=10,AB=8,
∴AE=6,
∴OE=10﹣6=4,
∴E点坐标为(4,0);
在Rt△ODE中,设DE=x,则OD=OC﹣DC=OC﹣DE=8﹣x,
∴x2=42+(8﹣x)2,解得x=5,
在Rt△BDE中,
BD= =5
=5 ;
②以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,如图:
∴B′的坐标为(10,﹣8),DD′=MN=4.5,
∴D′的坐标为(4.5,3),
设直线D′B′的解析式为y=kx+b,
把B′(10,﹣8),D′(4.5,3)代入得
10k+b=﹣8,4.5k+b=3,
解得k=﹣2,b=12,
∴直线D′B′的解析式为y=﹣2x+12,
令y=0,得﹣2x+12=0,解得x=6,
∴M(1.5,0);N(6,0).
(2)过点H作HM⊥BC于M,则MG=HG﹣x,
∵△GCF沿GF折叠得到△GHF,
∴HG=CG,故MG可表示为CG﹣x,
在Rt△HMG中,HG2=MG2+MH2,即HG2=(CG﹣x)2+64,
解得:CG=
;
②以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,如图:
∴B′的坐标为(10,﹣8),DD′=MN=4.5,
∴D′的坐标为(4.5,3),
设直线D′B′的解析式为y=kx+b,
把B′(10,﹣8),D′(4.5,3)代入得
10k+b=﹣8,4.5k+b=3,
解得k=﹣2,b=12,
∴直线D′B′的解析式为y=﹣2x+12,
令y=0,得﹣2x+12=0,解得x=6,
∴M(1.5,0);N(6,0).
(2)过点H作HM⊥BC于M,则MG=HG﹣x,
∵△GCF沿GF折叠得到△GHF,
∴HG=CG,故MG可表示为CG﹣x,
在Rt△HMG中,HG2=MG2+MH2,即HG2=(CG﹣x)2+64,
解得:CG= ,
∴SOHGC=
,
∴SOHGC= (CG+OH)•OC=
(CG+OH)•OC= ,即y=
,即y= ,
点F与点O重合点G与点B重合、点F与点O重合分别是点F的两个极限,
1、点G与点B重合时,由①的结论可得,此时OH=4,
2、点F与点O重合时,OH=8,
综上可得:y=
,
点F与点O重合点G与点B重合、点F与点O重合分别是点F的两个极限,
1、点G与点B重合时,由①的结论可得,此时OH=4,
2、点F与点O重合时,OH=8,
综上可得:y= ,(4≤x≤8).
,(4≤x≤8).

 8.如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形ADMN的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是( )
8.如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形ADMN的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是( )
 A.
A. B.
B. C.
C. D.
D. 【解答】解:因为在直角梯形ABCD中,DC∥AB,∠A=90°,
所以四边形ANMD也是直角梯形,因此它的面积为
【解答】解:因为在直角梯形ABCD中,DC∥AB,∠A=90°,
所以四边形ANMD也是直角梯形,因此它的面积为 (DM+AN)×AD,因为DM=t,AN=28﹣2t,AD=4;
所以四边形AMND的面积y=
(DM+AN)×AD,因为DM=t,AN=28﹣2t,AD=4;
所以四边形AMND的面积y= (t+28﹣2t)×4=﹣2t+56.
因为当其中一个动点到达端点停止运动时,另一个动点也随之停止运动;
所以当N点到达A点时,2t=28,t=14;
所以自变量t的取值范围是0<t<14.
故选:D.
9.如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=
(t+28﹣2t)×4=﹣2t+56.
因为当其中一个动点到达端点停止运动时,另一个动点也随之停止运动;
所以当N点到达A点时,2t=28,t=14;
所以自变量t的取值范围是0<t<14.
故选:D.
9.如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD= ,∠C=45°,点P是BC边上一动点,设PB的长为x.
(1)当x的值为 时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为 时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
,∠C=45°,点P是BC边上一动点,设PB的长为x.
(1)当x的值为 时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)当x的值为 时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
 【解答】解:(1)如图,分别过A、D作AM⊥BC于M,DN⊥CB于N,
则四边形AMND是矩形,
∴AM=DN,AD=MN=5,
而CD=
【解答】解:(1)如图,分别过A、D作AM⊥BC于M,DN⊥CB于N,
则四边形AMND是矩形,
∴AM=DN,AD=MN=5,
而CD= ,∠C=45°,
∴DN=CN=CD•sin∠C=4
,∠C=45°,
∴DN=CN=CD•sin∠C=4 ×
× =4=AM,
∴BM=CB﹣CN﹣MN=3,
若点P、A、D、E为顶点的四边形为直角梯形,
则∠APC=90°或∠DEB=90°,
当∠APC=90°时,
∴P与M重合,
∴BP=BM=3;
当∠DPB=90°时,P与N重合,
∴BP=BN=8;
故当x的值为3或8时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)若以点P、A、D、E为顶点的四边形为平行四边形,那么AD=PE,
有两种情况:①当P在E的左边,
∵E是BC的中点,
∴BE=6,
∴BP=BE﹣PE=6﹣5=1;
②当P在E的右边,
BP=BE+PE=6+5=11;
故当x的值为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)由(2)知,①当BP=1时,此时CN=DN=4,NE=6﹣4=2,
∴DE=
=4=AM,
∴BM=CB﹣CN﹣MN=3,
若点P、A、D、E为顶点的四边形为直角梯形,
则∠APC=90°或∠DEB=90°,
当∠APC=90°时,
∴P与M重合,
∴BP=BM=3;
当∠DPB=90°时,P与N重合,
∴BP=BN=8;
故当x的值为3或8时,以点P、A、D、E为顶点的四边形为直角梯形;
(2)若以点P、A、D、E为顶点的四边形为平行四边形,那么AD=PE,
有两种情况:①当P在E的左边,
∵E是BC的中点,
∴BE=6,
∴BP=BE﹣PE=6﹣5=1;
②当P在E的右边,
BP=BE+PE=6+5=11;
故当x的值为1或11时,以点P、A、D、E为顶点的四边形为平行四边形;
(3)由(2)知,①当BP=1时,此时CN=DN=4,NE=6﹣4=2,
∴DE= =
= =2
=2 ≠AD,故不能构成菱形.
②当BP′=11时,以点P′、A、D、E为顶点的四边形是平行四边形
∴EP′=AD=5,
过D作DN⊥BC于N,
∵CD=
≠AD,故不能构成菱形.
②当BP′=11时,以点P′、A、D、E为顶点的四边形是平行四边形
∴EP′=AD=5,
过D作DN⊥BC于N,
∵CD= ,∠C=45°,
则DN=CN=4,
∴NP′=BP′﹣BN=BP′﹣(BC﹣CN)=11﹣12+4=3.
∴DP′=
,∠C=45°,
则DN=CN=4,
∴NP′=BP′﹣BN=BP′﹣(BC﹣CN)=11﹣12+4=3.
∴DP′= =
=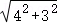 =5,
∴EP′=DP′,
故此时▱P′DAE是菱形.
即以点P、A、D、E为顶点的四边形能构成菱形;
=5,
∴EP′=DP′,
故此时▱P′DAE是菱形.
即以点P、A、D、E为顶点的四边形能构成菱形;

 10.已知:等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点,线段MN运动的时间为t秒.
(1)线段MN在运动的过程中,t为何值时,四边形MNQP恰为矩形并求出该矩形的面积;
(2)线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t,求四边形MNQP的面积S随运动时间t变化的函数关系式,并写出自变量t的取值范围.
10.已知:等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点,线段MN运动的时间为t秒.
(1)线段MN在运动的过程中,t为何值时,四边形MNQP恰为矩形并求出该矩形的面积;
(2)线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t,求四边形MNQP的面积S随运动时间t变化的函数关系式,并写出自变量t的取值范围.
 【解答】解:(1)过点C作CD⊥AB,垂足为D,则AD=2,
当MN运动到被CD垂直平分时,四边形MNQP是矩形,
即当AM=
【解答】解:(1)过点C作CD⊥AB,垂足为D,则AD=2,
当MN运动到被CD垂直平分时,四边形MNQP是矩形,
即当AM= 时,四边形MNQP是矩形,
∴t=
时,四边形MNQP是矩形,
∴t= 秒时,四边形MNQP是矩形,
∵PM=AMtan60°=
秒时,四边形MNQP是矩形,
∵PM=AMtan60°=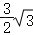 ,
PQ=MN=AB﹣2AM=4﹣3=1,
∴S四边形MNQP=PM•PQ=
,
PQ=MN=AB﹣2AM=4﹣3=1,
∴S四边形MNQP=PM•PQ=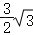 ;
(2)①当0<t≤1时,点P、Q都在AC上,并且四边形PMNQ为直角梯形,
在Rt△AMP中,
∵∠A=60°,AM=t,tan∠A=
;
(2)①当0<t≤1时,点P、Q都在AC上,并且四边形PMNQ为直角梯形,
在Rt△AMP中,
∵∠A=60°,AM=t,tan∠A=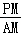 ,
∴PM=tan60°×AM=
,
∴PM=tan60°×AM= AM=
AM= t,
在Rt△ANQ中,
而AN=AM+MN=t+1,
∴QN=
t,
在Rt△ANQ中,
而AN=AM+MN=t+1,
∴QN= AN=
AN= (t+1),
∴S四边形MNQP=
(t+1),
∴S四边形MNQP= (PM+QN)MN=
(PM+QN)MN= [
[ t+
t+ (t+1)]=
(t+1)]= t+
t+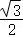 ;
②当1<t<2时,
点P在AC上,点Q在BC上,
PM=
;
②当1<t<2时,
点P在AC上,点Q在BC上,
PM= t,
BN=AB﹣AM﹣MN=4﹣1﹣t=3﹣t,
在Rt△BNQ中,
QN=
t,
BN=AB﹣AM﹣MN=4﹣1﹣t=3﹣t,
在Rt△BNQ中,
QN= BN=
BN= (3﹣t),
∴S四边形MNQP=
(3﹣t),
∴S四边形MNQP= (PM+QN)MN=
(PM+QN)MN= [
[ t+
t+ (3﹣t)]×1=
(3﹣t)]×1=
 ;
③当2≤t<3时,点P、Q都在BC上,
BM=4﹣t,BN=3﹣t,
∴PM=
;
③当2≤t<3时,点P、Q都在BC上,
BM=4﹣t,BN=3﹣t,
∴PM= BM=
BM= (4﹣t),QN=
(4﹣t),QN= BN=
BN= (3﹣t),
∴S四边形MNQP=
(3﹣t),
∴S四边形MNQP= (PM+QN)MN=
(PM+QN)MN= [
[ (3﹣t)+
(3﹣t)+ (4﹣t)]=
(4﹣t)]= ﹣
﹣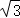 t.
综上所述:当0<t≤1时,S四边形MNQP=
t.
综上所述:当0<t≤1时,S四边形MNQP=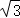 t+
t+ ;当1<t<2时,S四边形MNQP=
;当1<t<2时,S四边形MNQP=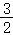
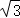 ;
当2≤t<3时,S四边形MNQP=
;
当2≤t<3时,S四边形MNQP= ﹣
﹣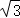 t. (10分)
t. (10分)



 11.如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A﹣B﹣C﹣D的路线作匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(秒).
①当t=5时,求出点P的坐标;
②若△OAP的面积为s,试求出s与t之间的函数关系式(并写出相应的自变量t的取值范围).
11.如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A﹣B﹣C﹣D的路线作匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(秒).
①当t=5时,求出点P的坐标;
②若△OAP的面积为s,试求出s与t之间的函数关系式(并写出相应的自变量t的取值范围).
 【解答】解:(1)P点从A点运动到D点所需的时间=(3+5+3)÷1=11(秒)
(2)①当t=5时,P点从A点运动到BC上,
过点P作PE⊥AD于点E.
此时A点到E点的距离=10,AB+BP=5,
∴BP=2
则PE=AB=3,AE=BP=2
∴OE=OA+AE=10+2=12
∴点P的坐标为(12,3).
②分三种情况:
i.0<t≤3时,点P在AB上运动,此时OA=2t,AP=t
∴s=
【解答】解:(1)P点从A点运动到D点所需的时间=(3+5+3)÷1=11(秒)
(2)①当t=5时,P点从A点运动到BC上,
过点P作PE⊥AD于点E.
此时A点到E点的距离=10,AB+BP=5,
∴BP=2
则PE=AB=3,AE=BP=2
∴OE=OA+AE=10+2=12
∴点P的坐标为(12,3).
②分三种情况:
i.0<t≤3时,点P在AB上运动,此时OA=2t,AP=t
∴s=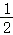 ×2t×t=t2
ii.3<t≤8时,点P在BC上运动,此时OA=2t
∴s=
×2t×t=t2
ii.3<t≤8时,点P在BC上运动,此时OA=2t
∴s=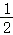 ×2t×3=3t
iii.8<t<11时,点P在CD上运动,此时OA=2t,AB+BC+CP=t
∴DP=(AB+BC+CD)﹣(AB+BC+CP)=11﹣t
∴s=
×2t×3=3t
iii.8<t<11时,点P在CD上运动,此时OA=2t,AB+BC+CP=t
∴DP=(AB+BC+CD)﹣(AB+BC+CP)=11﹣t
∴s=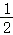 ×2t×(11﹣t)=﹣t2+11t
综上所述,s与t之间的函数关系式是:
当0<t≤3时,s=t2;
当3<t≤8时,s=3t;
当8<t<11时,s=﹣t2+11t.
×2t×(11﹣t)=﹣t2+11t
综上所述,s与t之间的函数关系式是:
当0<t≤3时,s=t2;
当3<t≤8时,s=3t;
当8<t<11时,s=﹣t2+11t.
 12.如图,在矩形OABC中,已知A,C两点的坐标分别为A(4,0),C(0,2),D为OA的中点.设点P是∠AOC平分线上的一个动点(不与点O重合).
(1)试证明:无论点P运动到何处,PC总与PD相等;
(2)当点P运动到与点B的距离最小时,求P的坐标;
(3)已知E(1,﹣1),当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长.
12.如图,在矩形OABC中,已知A,C两点的坐标分别为A(4,0),C(0,2),D为OA的中点.设点P是∠AOC平分线上的一个动点(不与点O重合).
(1)试证明:无论点P运动到何处,PC总与PD相等;
(2)当点P运动到与点B的距离最小时,求P的坐标;
(3)已知E(1,﹣1),当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长.
 【解答】(1)证明:∵A(4,0),C(0,2),D为OA的中点,
∴D点坐标为(2,0),
∴OC=OD,
又∵点P是∠AOC平分线上的一个动点(不与点O重合),
∴∠COP=∠DOP=45°,
∴△POC≌△POD,
∴PC=PD,
即无论点P运动到何处,PC总与PD相等;
(2)解:过B作BP垂直∠AOC的平分线于P点,过P点作PN⊥x轴于N,交BC于M点,OP交BC于H点,如图,
∵OP平分∠AOC,
∴∠COP=∠NOP=45°,
∴△PHM、△COH和△PON都是等腰直角三角形,
∴△PHB是等腰直角三角形,
∴PM垂直平分BH,
∴CH=CO=2,
∴BH=4﹣2=2,
∴PM=
【解答】(1)证明:∵A(4,0),C(0,2),D为OA的中点,
∴D点坐标为(2,0),
∴OC=OD,
又∵点P是∠AOC平分线上的一个动点(不与点O重合),
∴∠COP=∠DOP=45°,
∴△POC≌△POD,
∴PC=PD,
即无论点P运动到何处,PC总与PD相等;
(2)解:过B作BP垂直∠AOC的平分线于P点,过P点作PN⊥x轴于N,交BC于M点,OP交BC于H点,如图,
∵OP平分∠AOC,
∴∠COP=∠NOP=45°,
∴△PHM、△COH和△PON都是等腰直角三角形,
∴△PHB是等腰直角三角形,
∴PM垂直平分BH,
∴CH=CO=2,
∴BH=4﹣2=2,
∴PM= BH=1,
∴ON=PN=1+2=3,
∴P点坐标为(3,3);
(3)解:连CE交∠AOC的平分线于P点,连PD、CD,ED,如图,
∵OC=OD,OP平分直角AOC,
∴OP垂直平分CD,
∴PC=PD,
∴PD+PE=PC+PE=CE,
此时△PDE的周长最小,
设直线CE的解析式为y=kx+b(k≠0),
把C(0,2)、E(1,﹣1)分别代入得,b=2,k+b=﹣1,解得k=﹣3,b=2,
∴直线CE的解析式为y=﹣3x+2,
而P点的横纵坐标相等,设P(a,a),把P点坐标代入y=﹣3x+2得,a=﹣3a+2,解得a=
BH=1,
∴ON=PN=1+2=3,
∴P点坐标为(3,3);
(3)解:连CE交∠AOC的平分线于P点,连PD、CD,ED,如图,
∵OC=OD,OP平分直角AOC,
∴OP垂直平分CD,
∴PC=PD,
∴PD+PE=PC+PE=CE,
此时△PDE的周长最小,
设直线CE的解析式为y=kx+b(k≠0),
把C(0,2)、E(1,﹣1)分别代入得,b=2,k+b=﹣1,解得k=﹣3,b=2,
∴直线CE的解析式为y=﹣3x+2,
而P点的横纵坐标相等,设P(a,a),把P点坐标代入y=﹣3x+2得,a=﹣3a+2,解得a= ,
∴P点坐标为(
,
∴P点坐标为( ,
, ),
∵CE=
),
∵CE= =
= ,DE=
,DE=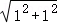 =
= ,
∴此时△PDE的周长=
,
∴此时△PDE的周长= +
+ .
.









 本文通过多个例题探讨了动点在四边形周长最短情况下的问题,涉及矩形、直角梯形等几何图形。在不同条件下,点P的位置会影响等腰三角形的形成,进而影响四边形的性质。通过解题过程,展示了如何找到点P的坐标以使△ODP成为腰长为5的等腰三角形,并探讨了动点在不同轨迹上如何影响四边形的周长和形状。
本文通过多个例题探讨了动点在四边形周长最短情况下的问题,涉及矩形、直角梯形等几何图形。在不同条件下,点P的位置会影响等腰三角形的形成,进而影响四边形的性质。通过解题过程,展示了如何找到点P的坐标以使△ODP成为腰长为5的等腰三角形,并探讨了动点在不同轨迹上如何影响四边形的周长和形状。
















 1360
1360

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








