实验四离散信号的DFT及其快速算法
一、实验目的
1.在学习DFT理论的基础上,通过本实验,加深对FFT的理解,体会二者之间的关系。2.熟悉应用FFT实现两个序列的线性卷积的方法。
二、实验原理
N点序列x[n] 的DFT和IDFT定义:
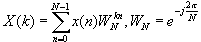
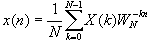
可以用函数U=fft(u,N)和u=ifft(U,N)计算N点序列的DFT正、反变换。
三、实验内容
1. x(n)=R5(n),求N分别取8,32时的X(k),最后绘出图形。
离散傅立叶变换函数的MATLAB实现如下:
N=8;
x=[ones(1,5),zeros(1,N-5)];
n=0:N-1;
X=dft(x,N);
magX=abs(X);
phaX=angle(X)*180/pi;
k=(0:length(magX)'-1)*N/length(magX);
subplot(2,2,1);stem(n,x);title('x(n)—8点');
subplot(2,2,2);stem(k,magX);axis([0,8,0,6]);title('|X(k)|--8点');
N=32;
x=[ones(1,5),zeros(1,N-5)];
n=0:N-1;
X=dft(x,N);
magX=abs(X);
phaX=angle(X)*180/pi;
k=(0:length(magX)'-1)*N/length(magX);
subplot(2,2,3);stem(n,x);title('x(n)—32点');
subplot(2,2,4);stem(k,magX);axis([0,32,0,5]);title('|x(k)|--32点');







 本实验通过MATLAB实现离散信号的离散傅立叶变换(DFT)及快速傅立叶变换(FFT),深入理解两者的关系,并掌握利用FFT进行线性卷积的方法。
本实验通过MATLAB实现离散信号的离散傅立叶变换(DFT)及快速傅立叶变换(FFT),深入理解两者的关系,并掌握利用FFT进行线性卷积的方法。
















 2653
2653

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








