多元高斯分布(多元正态分布)简介
标签:#正态分布##统计基础##高斯分布#
时间:2017-01-28 23:02:43
作者:小木
高斯分布(Gaussian Distribution),也称作是正态分布(Normal Distribution),是一种非常常见的分布,对于一元高斯分布(Univariate Gaussian Distribution)我们比较熟悉,对于高斯分布的多元形式有很多人不太理解。我们将简单介绍一下多元高斯分布的相关性质。这篇博客的材料主要来源Andrew Ng在斯坦福机器学习课的材料。[[1]][1]
[1]: http://cs229.stanford.edu/materials.html "斯坦福机器学习课程材料"
多元高斯分布(Multivariate Gaussian Distribution)的形式很简单,就是一元高斯分布的在向量形式的推广。我们把向量$X=[X_1,X_2,...,X_n]^T$称作是均值为$\mu \in \bold{R}^n$,协方差矩阵为$\Sigma \in S^n$的多元高斯分布,如果它具有如下概率密度函数的形式:
```math
p(x;\mu , \Sigma)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))
```
[TOC]
#### 一、多元高斯分布与一元高斯分布的关系
首先,我们回顾一下一元正态分布的形式,其概率密度函数如下:
```math
p(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{1}{2\sigma^2}(x-\mu)^2)
```
这里指数函数的参数$(-\frac{1}{2\sigma^2}(x-\mu)^2)$是一个关于x的二次项式函数。由于二次项的系数为负,因此它是抛物线开口向下的函数。此外,最前面的系数是$\frac{1}{\sqrt{2\pi}\sigma}$是与x无关的形式,因此我们可以把它当做是一个“正规化因子”(normalization factor),以保证:
```math
\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}\exp(-\frac{1}{2\sigma^2}(x-\mu)^2)=1
```
在多元高斯密度中,指数函数的参数是$-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)$,其中x是向量。由于$\Sigma$是正定的(positive definite),而任意正定矩阵的逆矩阵也是正定的。那么对于任意一个非零向量z,有$z^T \Sigma z>0$,也就是说对于任意的$x \neq \mu$,有:
```math
(x-\mu)^T\Sigma^{-1}(x-\mu) > 0
```
```math
-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu) < 0
```
与一元高斯分布类似,我们可以把该指数函数的参数当做一个开口向下的二次曲面(downward opening quadratic bowl)。在多元高斯密度函数中,前面的系数的形式比一元高斯分布要复杂很多,但它也同样的不依赖于x。因此,它也是一个正规化系数:
```math
-\frac{1}{(2\pi)^{n/2}|\Sigma|^{1/2}}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\ldots\int_{-\infty}^{\infty}\exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)) dx_1 dx_2 \ldots dx_n = 1
```

#### 二、协方差矩阵(The covariance matrix)
协方差矩阵的概念对理解多元高斯分布来说非常重要。回忆一下,对于一对随机变量X和Y,它们的协方差矩阵定义如下:
```math
Cov[X,Y]=E[(X-E[X])(Y-E[Y])]=E[XY]-E[X]E[Y]
```
对于多个变量来说,协方差矩阵是一个非常简洁的表达变量关系的方式。通常,我们用$\Sigma$表示协方差矩阵,它是一个$n \times n$的矩阵,其中第$(i,j)$的位置表示$Cov[X_i,X_j]$。下面还有一些命题,可以帮助我们理解一个随机向量X的协方差矩阵。
**命题1:**对于任意一个随机向量X,其均值为$\mu$,协方差为$\Sigma$,我们有:
```math
\Sigma = E[(X-\mu)(X-\mu)^T]=E[XX^T]-\mu\mu^T
```
在多元高斯分布的定义中,我们要求协方差矩阵是一个对称的正定矩阵。为什么有这个限制存在呢?实际上,对于任意的一个随机向量的协方差矩阵,它都是对称的半正定矩阵。
**命题2:**假设$\Sigma$是一个随机向量X的协方差矩阵,那么,$\Sigma$一定是一个对称的半正定矩阵。证明如下:
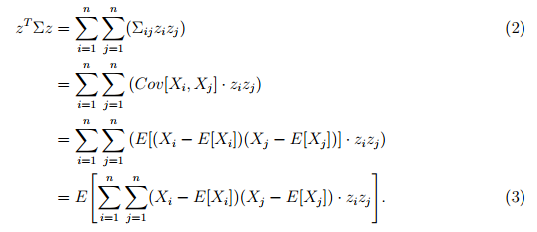
#### 三、对角协方差矩阵的例子
为了直观地理解一个多元高斯分布是什么样的,我们以最简单的n=2为例说明,并且我们假设其协方差矩阵是对角阵:
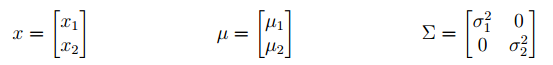
那么,其多元高斯密度函数的形式如下:
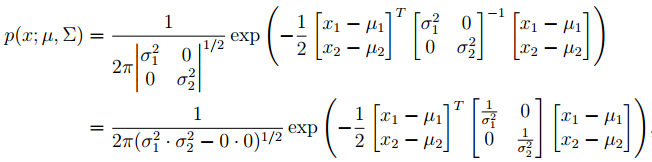
继续:
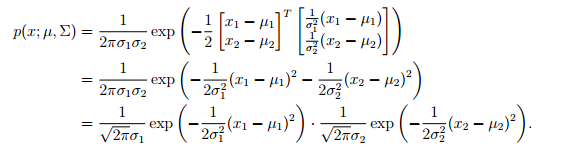
最后一行我们可以看出,这个二元高斯分布的密度函数就是两个独立的高斯密度乘积形式。也就是说,更一般的情况,当协方差矩阵是对角阵的时候,多元高斯分布就是一组相互独立的一元高斯分布的组合。
#### 四、等量线
另一个理解多元高斯分布的方法是从其等量线的形状来看。对于一个函数$f:R^2 \to R$,其等量线是如下形式的集合:
```math
{x \in R^2 : f(x)=c}
```
##### 4.1 等量线的形状
一个多元高斯分布的等量线是什么样的?我们依然以前面的二元对角协方差矩阵为例。让我们考虑某些常量情况下的等量线:
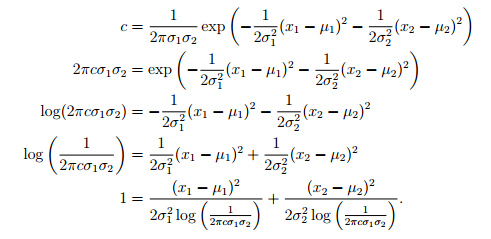
我们可以定义:

那么,它服从:
```math
1=(\frac{x_1-\mu}{r_1})^2+(\frac{x_2-\mu}{r_2})^2
```
这个形式应该比较熟悉了,就是高中解析几何里面的轴对称的椭圆了。
#####4.2 坐标轴长度
为了更好的理解等量线如何随着多元高斯分布的变化而变化,我们看一下在高斯密度函数的峰值位置,也就是$c=1/e$时,$r_1$和$r_2$的位置。首先我们通过公式4可以看到,当$x_1=\mu_1$且$x_2=\mu_2$到时候,高斯密度是位置最高,为$1/(2\pi\sigma_1\sigma_2)$。
然后,我们把$c=\frac{1}{e}\frac{1}{2\pi\sigma_1\sigma_2}$代入上式,我们有:
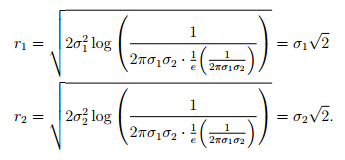
从这个地方我们看出,坐标轴长度与标准差$\sigma_i$成一定比例。这样容易理解,如果某些随机变量$x_i$比较小,那么高斯分布在那个维度上的线就越紧密,因此,半径$r_i$就更小。
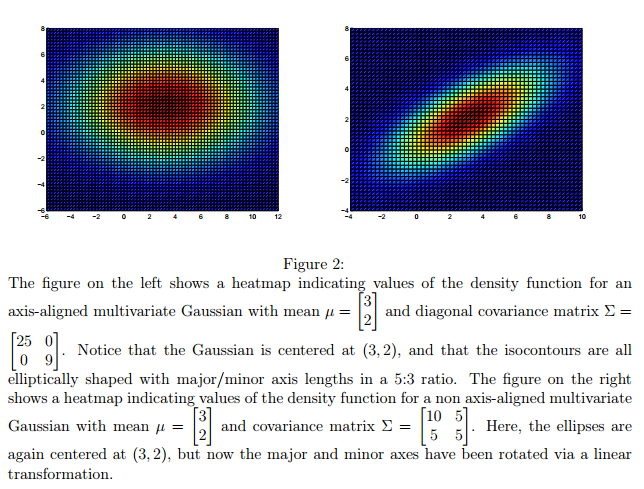
##### 4.3 非对角阵的情况,更高维的情况
显然,上述推到都是依赖于假设$\Sigma$是对角阵。然而,在非对角阵的情况下,图形也是类似的,只是轴对称的椭圆变成了一个变形的椭圆。
五、线性变换的解释
在最后几节里,我们将主要关注拥有对角协方差矩阵的多元高斯分布的一些特性。我们知道,对于对角协方差矩阵,我们可以把一个多元高斯分布看作是n个独立高斯分布的集合。在这里,我们将进一步了解其中的特性。
本节的最关键结果就是下面的理论:
**理论1:如果$X\sim N(\mu,\Sigma)$,且其协方差矩阵是对角的正定矩阵,那么一定存在一个矩阵$B \in R^{n \times n}$使我们可以定义$Z=B^{-1}(B-\mu)$,有$Z \sim N(0,I)$。**
如何理解这个理论呢?注意到,如果$Z\sim N(0,I)$,那么使用第4节的分析我们可以得到,Z是n个独立标准正太随机变量的集合。也就是,如果$Z=B^{-1}(X-\mu)$,那么,$X=BZ+\mu$。因此,该理论说明,任意多元高斯分布X都可以运用线性变换($X=BZ+\mu$)把它变成一组n个独立的标准正态分布变量的集合。





















 305
305

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








