Ensemble-boosting（三）

写在前面

上面整理的前向分布算法、adaboost、提升树算法、GBDT&GBRT。
这篇整理XGBoost

约定

假设存在数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} D={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，其中， y i ∈ { − 1 , 1 } y_i\in\{-1,1\} yi​∈{−1,1}

XGBoost VS GBDT

天奇大佬，分享了PPT和论文，超级棒。
大佬从理论，尤其是工程方面实现了对GBDT的一次极大改进，不仅是预测精度而且训练速度加快很多。
全称：Extreme Gradient boosting
我以为： X Gradient boosting 类似于X战警，哈哈哈哈嗝。
先吹嘘一波天奇大佬，
【文中提到，XGBoost，这个系统的效果已经被大量的机器学习和数据挖掘竞赛所验证。以Kaggle为例，2015年29组优胜方案中17组使用了XGBoost。这其中，8组只是使用了XGBoost去训练模型，其他大部分都是将XGBoost和神经网络做集成。作为对比，第二受欢迎的工具，深度神经网络，有11组采用。在KDDCup 2015中，top-10 每一组都使用了XGBoost。】
1、泰勒二阶展开式:$f(x+\Delta x)=f(x)+f^{\prime }(x)\Delta x+\frac{1}{2}{f}^{\prime \prime }(x){\Delta }^{2}x$
$$obj=\sum _{i=1}^{N}L(y_i;{\widehat{y_i}}^{t-1}+f_t(x_i))+\Omega (f_t)+constant\text{\hspace{1em}(1)}$$
将$f_t(x_i)$看作$\Delta x$，对公式（1）展开可得，
$$obj=\sum _{i=1}^{N}L(y_i;{\widehat{y_i}}^{t-1})+g_i{f}_t(x_i)+h_i{f}_t^2(x_i)+\Omega (f_t)+constant$$
记$g_i={\partial }_{{\widehat{y_i}}^{t-1}}L(y_i;{\widehat{y_i}}^{t-1})$,$h_i={\partial }_{{\widehat{y_i}}^{t-1}}^{2}L(y_i;{\widehat{y_i}}^{t-1})$。
去掉常量：
$$obj=\sum _{i=1}^N{g}_i{f}_t(x_i)+h_i{f}_t^2(x_i)\text{\hspace{1em}(2)}$$
以上，用二阶展开替代之前gbdt的一阶展开（求导）的结果，可以获得更高的精度，收敛更快（不仅加速度最大，而且加速度的增大方向也是最大的。）
2、重新定义树的结构,按叶子加和：
adaboost,gbdt等：
$$T(x;{\theta }_m)=\sum _{i=1}^N{w}_{j}I(x_i\in C_j))$$
xgboost：
定义叶节点的分数（输出值）向量：$w_i\in R^T$,$T$是叶节点数量。
将实例映射到叶节点索引的函数： q : R d − > { 1 , 2 , . . . , T } q:R^d->\{{1,2,...,T}\} q:Rd−>{1,2,...,T}，
x代表所有样本，

$$f_t(x)=w_{q(x)}$$
3、修改正则项（minor）,论文中说是很小的修改，但在实践中效果不错。相比于gbdt增加了一项叶节点的权重和，当然还有其它的定义方式，其中$T_t$表示某棵树的叶节点数量 ，还记得gbdt怎么更新叶节点的输出吗？选择使得Loss function 最小的输出。
$$\Omega (f_t)=\gamma T_t+\lambda \frac{1}{2}\sum _{j=1}^T{w}_j^2$$
4、上面说清楚了，天奇大佬定义的损失函数包含哪些内容，那么这里的二阶导数除了收敛更快，精度更高之外，还有更大的目的是为了根据自定义损失函数，实现一个可扩展的损失函数。对于公式（2），
$$obj=\sum _{i=1}^N{g}_i{f}_t(x_i)+h_i{f}_t^2(x_i)+\Omega (f_t)+constant$$
定义节点$j$的样本集合： I j = { i ∣ q ( x i ) = j } I_j=\{i|q(x_i)=j\} Ij​={i∣q(xi​)=j}
$$obj=\sum _{i=1}^N{g}_i{f}_t(x_i)+h_i{f}_t^2(x_i)+\gamma T_t+\lambda \frac{1}{2}\sum _{j=1}^T{w}_j^2+constant$$
$$obj=\sum _{i=1}^N{g}_i{w}_{q(x_i)}+h_i{w}_{q(x_i)}^2+\gamma T_t+\lambda \frac{1}{2}\sum _{j=1}^T{w}_j^2+constant$$
$$obj=\sum _{j=1}^T[(\sum _{i\in I_j}{g}_i)w_j+\frac{1}{2}((\sum _{i\in I_j}{h}_i)+\lambda )w_j]+\gamma T_t$$
假设树的结构固定，即$\gamma T_t$是常量，记$G_j={\sum }_{i\in I_j}{g}_i$，$H_j={\sum }_{i\in I_j}{h}_i$
$$obj=\sum _{j=1}^T[G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j]+\gamma T_t$$
存在单变量二次函数的两个结论：


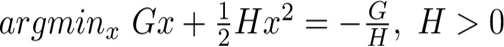
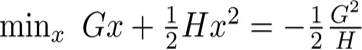
最终，天奇大佬，推出，每个叶子的最优分数和最终的loss函数的分别是，
$$w_j^{\ast }=-\frac{G_j}{H_j+\lambda }$$
$$obj=-\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }++\gamma T_j\text{\hspace{1em}(3)}$$
观察一下公式（3），对于任意损失函数，只要可二阶导，都可以用该公式计算最终的loss。得到了极小值的解析解。实现了可扩展性。而且工程实现中，基模型还可以是线性模型。具体可以看一下这里树的定义，是叶子节点的加权和，和线性模型很相似了。

XGBoost 工程优化

1、Why so fast?

• 树的生成算法

• exact greedy algorithm,预排序+线性搜索所有特征切分点（CART回归树也是这样做的），预排序用空间换时间。

• 构建直方图：对连续特征做离散化，xgb的工程实现中，给出了两种方式global, local。global在建树之前建proposal，对于所有层保持一致。local,每一次分割后会更新 proposal

2、Sparse aware?
对于missing data 分别计算该样本划分到左右节点的增益，选择较大的增益节点作为划分节点，也可以设定默认划分方向。
feature zero：在分布式系统上的实现中，用直方图做分桶。
类别特征：one-hot

3、预排序时间太长，或者data无法完全放进内存。

• exact greedy algorithm: sort all data in one block
• approximate algorithm: save into several blocks. 每个block 与data中的列的子集（仅部分特征）相关。

4、对于工程上的优化，还需要仔细读API,和论文以及源码才能弄清楚，用的话还是api比较重要。

小问题

1、为什么展开用二阶导？（为什么不用三阶导呢）？
我的理解：
二阶导相比于一阶导来说，精度更高，同时会加快模型训练速度。
此外，天奇大佬根据二阶导的loss function，推导了一个叶子节点和loss function的一般解，而只用到了上一次迭代输出模型的梯度信息。
斗胆猜测一下，不用三阶导可能因为：二阶导足够用了，三阶导增加计算量的花费>对精度的提高。
2、xgb的直方图和LGB的直方图有什么区别呢？
下一篇