gradient-TD

A Convergent O(n) Algorithm for Off-policy Temporal-difference Learning with Linear Function Approximation

我们介绍了第一个时间差分学习算法，该算法对于任何有限马尔科夫决策过程、行为策略和目标策略在线性函数近似和Off-policy训练下是稳定的，其复杂度在参数数量上是线性的。梯度时间差分（GTD）算法估计了TD(0)算法的e expected update vector，并对其L2范数进行随机梯度下降。我们证明算法是稳定和收敛的，与LSTD找到的最小二乘解决方案相同，但没有LSTD的二次计算复杂性。

1 Off-policy learning methods

在目前的工作之前，将四个单独的理想算法结合起来，就无法避免不稳定的可能性。1）off-policy更新，2）时间差分学习，3）线性函数近似，4）内存和每步时间计算的线性复杂性（linear complexity in memory and per-time-step computation.）。如果放弃这四个中的任何一个，那么就可以相对容易地获得稳定的方法。但是每一个方法都带来了价值，我们不愿意放弃任何一个。在本文中，我们提出了第一个实现结合四个理想方法的算法，并且都是稳定和收敛的。

此外，我们的算法不使用重要性抽样，方差也低。我们的算法可以被看作是在一个新的目标函数中进行随机梯度下降，该函数的最优值是最小二乘法的TD解。我们的算法可以被广泛地描述为TD(0)的梯度下降版本，因此我们称之为GTD(0)。

2 Sub-sampling and i.i.d. formulations of temporal-difference learning

在这一节中，我们提出了单步时间差分学习的off-policy policy-evaluation问题，即数据由独立、同分布（i.i.d.）的样本组成。我们考虑标准的强化学习框架。在一连串的离散时间步骤t=1，2，…中，环境处于一个状态$s_t\in \mathcal{S}$，agent选择一个动作$a_t\in \mathcal{A}$，奖励为$r_t\in \mathcal{R}$，并转换到下一个状态$s_{t+1}\in \mathcal{S}$。状态转换是随机的，取决于接下来的状态和动作。奖励是随机的，取决于前一个状态和动作，以及下一个状态。产生动作的agent过程被称为行为策略。首先，我们假设有一个确定的目标策略$\pi ：\mathcal{S}\to \mathcal{A}$，目标是学习其状态值函数的近似值:

其中γ∈[0,1)为贴现率。

在很多问题中，状态集太大，对每个状态的值进行近似是不现实的。这里我们考虑线性函数近似，在这种情况下，状态被映射到维度少于状态数量的特征向量上。也就是说，对于每个状态$s\in \mathcal{S}$，有一个相应的特征向量$\varphi (s)\in {\mathbb{R}}^n$，$n<<|S|$。然后，要求对价值函数的近似在特征向量和相应的参数向量$\theta \in {\mathbb{R}}^n$中是线性的( The approximation to the value function is then required to be linear in the feature vectors and a corresponding parameter vector $\theta \in {\mathbb{R}}^n$😃:

环境和行为策略共同产生了一个状态、动作和奖励序列$s_1,a_1,r_1,s_2,a_2,r_2,...$，我们可以将其分解为4元组，$(s_1,a_1,r_1,s^{\prime }1)，(s_2,a_2,r_2,s_2^{\prime })，....，$其中$s_t^{\prime }=s_{t+1}$。

稍微滥用一下符号，让$s_k$表示采取on-policy action动作的第k个状态（With a slight abuse of notation, let sk denote the kth state in which an on-policy action was taken），让$r_k$和$s_k^{\prime }$表示相关的奖励和下一个状态。第k个on-policy transition，表示为$(s_k,r_k,s_k^{\prime })$。学习算法可用的相应数据是triple $(\varphi (s_k)，r_k，\varphi (s_k^{\prime }))$。

假设行为策略下的MDP是遍历性的(ergodic)，因此它决定了一个stationary state-occupancy distribution μ ( s ) = l i m k → ∞ P r { s k = s } μ(s)=lim_{k→∞}P_r\{s_k = s\} μ(s)=limk→∞​Pr​{sk​=s}。对于任何状态s，MDP和目标策略共同决定了一个N×N的state-transition-probability matrix P，其中 p s s ′ = P r { s k ′ = s ′ ∣ s k = s } p_{ss'} = P_r\{s'_k =s'|s_k = s\} pss′​=Pr​{sk′​=s′∣sk​=s}，和一个N×1的奖励向量R，其中$R_s=\mathbb{E}[r_k|s_k=s]$。这两个一起完全描述了 on-policy transitions的统计数据， $(\varphi (s_k)，r_k，\varphi (s_k^{\prime }))$序列中的所有样本都遵循这些统计数据。该问题仍然具有马尔可夫结构，即样本转换之间存在时间上的依赖性。在我们的分析中，我们首先考虑一个没有这种依赖关系的表述，即i.i.d.情况，然后证明我们的结果可以扩展到其他情况。

在 i.i.d公式中，状态$s_k$独立且同分布的，是根据一个概率分布μ生成的。从每个$s_k$中，根据 on-policy state-transition matrix P生成一个相应的$s_k^{\prime }$，$r_k$由一个的任意有界分布生成的，期望值为$R_{s_k}$。近似值函数最终学习的i.i.d.数据序列是$(\varphi (s_k)，r_k，\varphi (s_k^{\prime }))$，k=1，2，…。此外，由于每个样本都是i.i.d.，因此我们可以删除索讨论随机变量$(\varphi ，r,{\varphi }^{\prime })$。

学习的目标还有待确定。linear setting TD误差为

在此基础上，我们将一步线性TD解定义为关于$\theta$的值

其中$A=\mathbb{E}[\varphi (\varphi -\gamma {\varphi }^{\prime }{)}^T]，b=\mathbb{E}[r\varphi ]$。这是线性TD(0)算法（Sutton 1988）在on-policy训练下收敛的参数值。TD解总是线性TD(0)算法的一个不动点，但在off-policy训练下它可能不是稳定的;如果θ不完全满足(4)，则TD(0)算法可能使其偏离期望值，最终发散到无穷大。

3 The GTD(0) algorithm

接下来我们将介绍GTD(0)算法的想法和梯度下降推导。如上所述，向量$\mathbb{E}[\delta \varphi ]$可视为当前解θ中的误差。所以它的范数是我们离TD解有多远的度量。我们使用该向量的L2范数作为我们的目标函数：

当$\mathbb{E}[\delta \varphi ]$=0时，它的最小值为0。这个目标函数的梯度为

最后一个等式由(3)带入得到

最后一个方程是我们分析的关键。我们想采取随机梯度下降的方法，即在每个样本上做一个小的改变，以使预期的更新方向与梯度方向相反。如果梯度可以写成一个期望值，这是很简单的，但是这里是两个期望值的乘积。我们不能同时对它们进行抽样，因为抽样乘积会因为它们的相关性而产生偏差（One cannot sample both of them because the sample product will be biased by their correlation）。

然而，可以存储其中一个期望的长期、准稳定的估计值，然后对另一个期望进行采样。问题是，哪个期望值应该被估计和存储，哪个应该被采样？这两种方式似乎都能带来有趣的学习算法。（However, one could store a long-term, quasi-stationary estimate of either of the expectations and then sample the other. The question is, which expectation should be estimated and stored, and which should be sampled? Both ways seem to lead to interesting learning algorithms.）

首先让我们考虑一下通过forming and storing第一个期望值的单独估计得到的算法，也就是矩阵$A=\mathbb{E}[\varphi (\varphi -\gamma {\varphi }^{\prime }{)}^T]$的算法。 根据经验，该矩阵很容易估算为所有先前观察到的样本 outer products $\varphi (\varphi -\gamma {\varphi }^{\prime }{)}^T$的简单算术平均. 注意，在任何固定的策略评估问题中，A是一个 stationary statistic；它不依赖于θ，如果θ发生变化，也不需要重新估计。设$A_k$为观察前k个样本后的估计数$({\varphi }_1,r_1，{\varphi }_1^{\prime })，\dots ({\varphi }_k,r_k,{\varphi }_k^{\prime })$。然后该算法定义为

其中${\theta }_1$是任意的，${\delta }_k=r_k+\gamma {\theta }_k^T{\varphi }_k^{\prime }-{\theta }_k^T{\varphi }_k$，而αk > 0是步长参数，可能随时间而减少。我们称这种算法为$A^{T}TD(0)$，因为它基本上是传统的TD(0)前缀以矩阵$A^T$的估计。尽管我们发现这个算法很有趣，但我们在这里没有进一步考虑它，因为它每个时间步长需要O(n2)内存和计算。

估计梯度(6)的随机逼近算法的第种方法是形成并存储( form and store)第二个期望的估计值，即向量$\mathbb{E}[\delta \varphi ]$，并对第一个期望进行采样，$\mathbb{E}[\varphi (\varphi -\gamma {\varphi }^{\prime }{)}^T]$的。让$u_k$表示观察前k-1个样本后对$\mathbb{E}[\delta \varphi ]$的估计，$u_1=0$。GTD(0)算法定义为

其中${\theta }_1$是任意的，${\delta }_k$和(3)中的${\theta }_k$相同（δk is as in (3) using θk），αk>0和βk>0是步长参数，可能随时间减少。请注意，如果乘积是right-to-left，那么整个计算在每个时间步长是O(n)（Notice that if the product is formed right-to-left, then the entire computation is O(n) per time step）。

4 Convergence

论文

5 Extensions

5.1 Q-evaluation

GTD算法立即扩展到action-value函数的off-policy学习的情况。为此，假设遵循一个行为政策${\pi }_b$，以正概率对每个状态下的所有行动进行采样。在这种情况下，基础函数(basis functions)依赖于状态和动作：$\varphi :\mathcal{S}\times \mathcal{A}\to {\mathbb{R}}^n$。除了${\varphi }_t$和${\varphi }_t^{\prime }$被重新定义如下，学习方程没有变化：

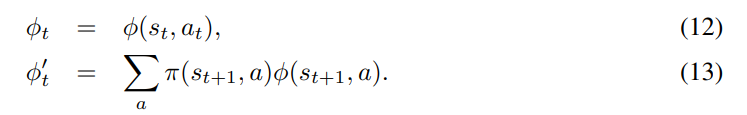
这里π(s, a)是在目标策略π下，在状态s下选择行动a的概率。 让我们把得到的算法称为 “one-step gradient-based Q-evaluation”，或GQE(0)。

5.2 Stochastic target policies and other sample weightings

我们的方法很容易被推广到随机目标策略上，方法是用一个样本加权过程取代第2节中描述的子抽样过程。也就是说，我们不是根据所采取的动作是否符合确定的策略来包括或排除transitions，而是包括所有的transitions，但给每个transitions一个权重。例如，我们可以让时间步骤t的权重wt等于在目标政策下采取实际行动的概率π（st, at）。我们现在可以认为独立样本有四个部分（φk, rk, φ0k, wk），更新规则（9）和（10）被替换为
例如，我们可以让时间步长t的权重$w_t$等于在目标策略下实际采取行动的概率$\pi (s_t,a_t)$。我们可以考虑i.i.d. 样本现在有四个组件$({\varphi }_k,r_k，{\varphi }_k^{\prime }，w_k)$，将更新规则(9)和(10)替换为

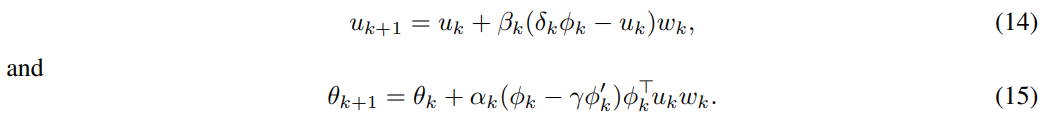
每个样本在期望值中也被$w_k$加权。有了这些变化，定理4.1和4.2适用于随机政策。重新加权实际上是对i.i.d.抽样分布$\mu$的调整，因此我们的结果成立，因为它们对所有μ都成立。选择$w_t=\pi (s_t,a_t)$只是一种可能性，值得注意的是，如果目标策略是确定性的，它与我们原来的情况是等同的。另一个自然的加权是$w_t=\pi (s_t,a_t)/{\pi }_b(s_t,a_t)$，其中${\pi }_b$是行为策略。这种加权可能会使TD方案（4）更好地匹配目标策略的价值函数（1）。