Fast Gradient-Descent Methods for Temporal-Difference Learning with Linear Function Approximation

Fast Gradient-Descent Methods for Temporal-Difference Learning with Linear Function Approximation

论文
gradient temporal difference（GTD）算法能够可靠地收敛，但与传统的线性TD相比，它可能非常慢。在本文中，我们介绍了两种具有更好收敛率的新的相关算法。

第一种算法，GTD2，与GTD一样被推导并证明是收敛的，但使用不同的目标函数，收敛速度明显加快（但仍不如传统TD快）。第二种新算法，带有梯度修正的线性TD，或称TDC，使用与传统TD相同的更新规则，除了一个初始化为0的附加项。在我们对small test problems和具有一百万个特征的计算机围棋应用的实验中，该算法的学习速度与传统的TD相当。这种算法似乎可以将线性TD扩展到off-policy学习中，并且在性能上没有任何损失，同时只需增加一倍计算要求。

1. Motivation

基于梯度下降和线性函数近似的时间差分方法构成了现代强化学习领域的核心部分，对其许多大规模应用至关重要。然而，最简单和最流行的方法，包括TD(λ)、Q-learning和Sarsa，都不是真正的梯度下降方法（Barnard 1993），因此，它们收敛的条件比梯度下降方法更不稳定。特别是，当这些方法与off-policy训练一起使用时，不能保证收敛（Baird 1995）。十多年来，寻找一种在大型应用中有效的线性函数近似的off-policy时间差分算法一直是强化学习中最重要的开放性问题之一。

对于这个问题，已经开发了几种非梯下降的方法，但没有一种是完全令人满意的。二阶方法，如LSTD(Bradtke & Barto 1996; Boyan 1999)，在一般条件下可以保证稳定，但其计算复杂度为$O(n^2)$，其中n为线性逼近器中使用的特征数，而TD(λ)和其他简单方法的计算复杂度为O(n)。在应用中，n往往太大（例如，计算机围棋中的n=$10^6$，Silver等人，2007），因此二阶方法是可行的。诸如iLSTD（Geramifard等人，2006）这样的增量方法将每个时间段的计算量减少到O(n)，但仍然需要$O(n^2)$内存。Precup及其同事（2001年；2006年）探索了基于重要性抽样的O(n)解决方案，但这些方法仍有可能出现不稳定，收敛缓慢，或只适用于特殊情况。在本文中，我们在Baird（1995；1999）和Sutton、Szepesvari和Maei（2009）的工作基础上，探索了真正的随机梯度下降算法，用于线性函数近似的时间差分学习。

2. Linear value-function approximation

每个时间t的状态是一个随机变量，表示为 s t ∈ { 1 ， 2 ， . . . ， N } s_t∈\{1，2，...，N\} st​∈{1，2，...，N}，状态转移概率为矩阵P。状态从$s_t$转移到$s_{t+1}$，奖励为$r_{t+1}$。我们试图学习参数为$\theta \in {\mathcal{R}}^n$的一个近似值函数$V_{\theta }:S\to \mathcal{R}$，使

其中${\varphi }_s\in {\mathcal{R}}^n$是状态s的特征向量，γ∈[0，1]是一个常数，称为贴现率。

在本文中，我们考虑单步时间差分学习（对应于TD（λ）中的λ=0），其中每个状态转换和相关奖励对θ有一个独立的更新。有几种与状态转换产生方式相对应的设置。例如，在on-policy设置中，状态转换直接来自马尔可夫链的持续演化。我们假设马尔科夫链是ergodic and uni-chain，所以存在一个极限分布d，使得$d_s=li{m}_{t\to \infty }P(s_t=s)$。

在on-policy情况下，d与 transition probabilities有关（特别是，我们知道$P^{T}d=d$），这传统TD等算法的收敛性至关重要。在本文中，我们考虑一个更一般的设置（在Sutton, Szepesvari & Maei 2009中介绍），其中每个transition的第一个状态是根据可能与P无关的任意分布d选择的（这相当于off-policy学习）。这定义了状态、下一个时刻状态和奖励随机变量的独立三元组的概率，表示为$(s_k,s_k^{\prime },r_k)$，以及相关的特征向量随机变量${\varphi }_k={\varphi }_{s_k}和{\varphi }_k^{\prime }={\varphi }_{s_k^{\prime }}$。根据这些，我们可以定义，例如， temporal-difference error：

其中${\alpha }_k$是一系列的 positive step-size parameters。

3. Objective functions

我们通过更新θ来最小化目标函数。那么，第一个问题是用什么作为目标函数？例如，一个自然的选择可能是近似值函数$V_{\theta }$和真实值函数$V$之间的平均平方误差（MSE），根据每个状态的出现频率在状态空间上进行平均。MSE的目标函数是

$||v|{|}_D^2=v^{T}Dv(a)$

$||v|{|}_D^2=v^{T}Dv$ is weighted by the matrix D that has the $d_s$ on its diagonal.

值函数V满足Bellman方程:

其中R是含有分量 E { r t + 1 ∣ s t = s } E\{r_{t+1} | s_t = s\} E{rt+1​∣st​=s}的向量，T被称为贝尔曼算子。均方贝尔曼误差：

然而，大多数时间差分算法，包括TD、LSTD和GTD，并不收敛到MSBE的最小值。To understand this, note that the Bellman operator follows the underlying state dynamics of the Markov chain, irrespective of the structure of the function approximator. As a result, $T{V}_{\theta }$ will typically not be representable as $V_{\theta }$ for any θ. Consider the projection operator $\Pi$ which takes any value function v and projects it to the nearest value function representable by the function approximator:

在线性结构中，其中$V_{\theta }={\Phi }_{\theta }$ ($\Phi$是行为${\varphi }_s$的矩阵)，投影算子是线性的，且与θ无关:

$V_{\theta }={\Phi }_{\theta }$ ($\Phi$是行为${\varphi }_s$的矩阵（where $\Phi$ is the matrix whose rows are the ${\varphi }_s$）)，投影算子是线性的，且与θ无关:
Off-Policy的近似方法
(b)

上述所有算法都能收敛到一个由投影和贝尔曼算子组成的fixpoint，也就是找到一个值，使得

We call this value of $\theta$ the TD fixpoint(TD不动点)。也就是说，我们用均方投影贝尔曼误差作为我们的目标函数:


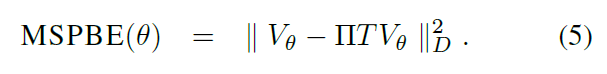
图1显示了这与MSBE目标函数之间的几何关系。虽然以前的许多工作都强调了实现TD fixpoint (4)的目标，但本工作似乎是第一个将MSPBE作为一个目标函数进行最小化的工作（但见Antos, Szepesv´ari and Munos 2008, p. 100）。

原始GTD算法的目标函数：

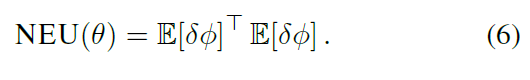
4. Derivation of the new algorithms

在本节中，我们在投影Bellman误差目标中推导出两种新的随机梯度下降算法
(5)首先建立相关期望与向量矩阵量之间的关系:

根据(b)式：

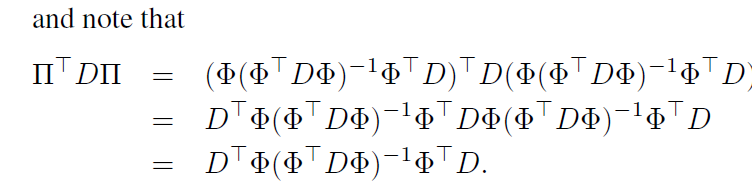
结合上式：

从这个形式可以看出，MSPBE与NEU(6)的区别仅仅在于包含了特征协方差矩阵的逆。与之前的工作一样（Sutton, Szepesvari & Maei 2009），我们使用第二个可修改参数$w\in {\mathcal{R}}^n$来近似目标函数梯度中除一个期望外的所有期望的准平稳估计(to form a quasi-stationary estimate of all but one of the expectations in the gradient of the objective function)，从而避免了对两个独立样本的需求。这里我们使用一个传统的线性预测器，使w近似于

As in prior work (Sutton, Szepesvari & Maei 2009) we use a second modifiable parameter $w\in {\mathcal{R}}^n$ to form a quasi-stationary estimate of all but one of the expectations in the gradient of the objective function, thereby avoiding the need for two independent samples. Here we use a conventional linear predictor which causes w to approximate


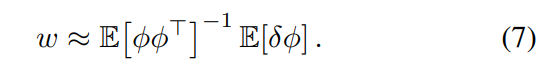
第二个新算法的推导从相同的梯度表达式开始，然后采用稍微不同的路径:

然后对其进行采样，形成以下O(n)算法，我们称之为带梯度校正的TD(TD with gradient correction)，简称TDC

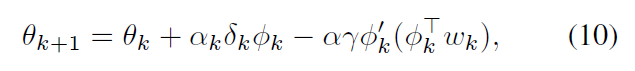
其中$w_k$由(9)产生，如同GTD2。注意，对${\theta }_k$的更新是两个项的总和，第一个项与传统线性TD的更新（2）完全相同。第二项基本上是对TD更新的调整或修正，使其遵循MSPBE目标函数的梯度。如果第二个参数向量被初始化为$w_0=0$，并且$\beta )k$很小，那么这个算法一开始就会做出与传统线性TD几乎相同的更新。还要注意的是，在${\theta }_k$收敛后，$w_k$将再次收敛为零。

Proof and Result

论文