强化学习系列（十二）：Eligibility Traces

一、前言

Eligibility Traces是强化学习的基本原理之一。例如TD($\lambda$)算法，($\lambda$)表示eligibility traces的使用情况。几乎所有TD方法，如 Q-Learning或Sarsa，都可以和eligibility traces结合起来生成更高效通用的方法。

Eligibility Traces可以用于泛化TD和MC（蒙特卡罗）方法。当用eligibility traces增强TD后，会产生一系列方法，包括两个极端的方法：MC（$\lambda = 1$）和 one step TD（$\lambda = 0$）。位于两者中间的方法比这两方法好。Eligibility Traces也提供了将MC方法用于在线连续问题的方式。

第7章中，我们介绍了一种连接TD和MC方法的n-step TD。Eligibility Traces的连接方式提供了一种更为优雅的算法机制，有很大的计算优势。该机制包含一个短期记忆向量，Eligibility Traces $\mathbf z_t \in R^d$，对应一个长期权重向量 $\mathbf w_t \in R^d$。基本思想是$\mathbf w_t$中参与生成estimated value的元素对应的 $\mathbf z_t$中的元素波动并逐渐衰减。如果在trace衰减到0之前，TD error不为零时，则该$\mathbf w_t$中参与生成estimated value的元素会一直持续学习。trace-decay 参数$\lambda \in [0,1]$，表示trace的后退速度。

与n-step方法相比：

• Eligibility Traces方法只需要存储一个trace vector，而不是n个最新的feature vectors。
• 而且学习过程是连续且时间均匀的，不会有延迟。不需要在episode结束时刻立即进行所有运算。
• 学习可以立刻影响行为，不需要n step后才延迟生效。

Eligibility Traces 表明学习算法换种方式进行运算可能会获得一定的计算优势。很多算法都比较符合自然逻辑，向前看几步，根据未来的预测调整当前的量，如MC算法根据future reward的所有量，来更新state，n-step TD根据next n rewards来更新。这种向前看的形式，称为 forward views。通常 forward views不太实用，因为更新依赖于当前不可得到的量。本章中，我们将介绍另一种类似的更新方式，有时甚至完全一样，采用eligibility trace从当前TD error 向后看最近经过的states。这种方式称为 backward views。

本章首先，从 state value和 prediction 问题说起，再将其扩展到action value和control 问题中。先讨论on-policy问题，再扩展到off-policy问题。重点讨论 linear function approximation。

二、The $\lambda$- return

第7章中定义了n-step return

对tabular learning而言，该式可作为 approximate SGD learning update 的update target。这个结论对n-step returns的平均值也成立，只要权重和为1，如$\frac{1}{2} G_{t:t+2} + \frac{1}{2} G_{t:t+4}$，这种组合return的方式和 n-step return 一样通过减小 TD error来更新，因此可以保证算法收敛。 Averaging方式可以衍生出一系列新算法，如将 one-step 和infinite-step return平均获得 TD和MC之间的另一种算法，通过将experience-based update 和 DP update 取平均值，可以将experience-based 和model-based 方法结合。

这种将简单元素取平均的更新方式叫做 compound update。$\frac{1}{2} G_{t:t+2} + \frac{1}{2} G_{t:t+4}$就是一种compound update，其backup 图如下：

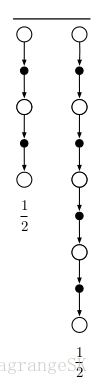
A compound update can only be done when the longest of its component
updates is complete。该更新只有在t+4时刻才能估计t时刻的值。一般会限制最长元素的长度，因为会延迟update的响应。

TD($\lambda$)算法是一种特殊的averaging n-step update，包括所有n-step updates，权重系数分别为$\lambda^{n-1}$，$\lambda \in [0,1]$，由（1-$\lambda$）归一化处理，$\lambda$-return 定义如下：

backup 图如图所示：

所有子n-step return的总和为$G_t$：

当$\lambda = 1$时，为MC方法的return，当$\lambda = 0$时，为one-step TD的 return。

现在定义以$\lambda$-return 为update target的第一个算法——off-line $\lambda$-return algorithm。在episode中，权重向量不变，episode结束时，整个off-line update 序列按照 semi-gradient rule更新：

$\lambda$-return 使得MC和one-step TD可以平顺过渡，以19-state random walk task(第七章例子）为例，和n-step TD 结果进行比较：

整体结果差不多，两个任务中，都是中间参数表现比较好，即n-step方法中n取中间值，$\lambda$-return算法中 $\lambda$ 取中间值。

目前我们讨论的方法都叫做 forward views算法。这什么意思呢？想向我们是一个拿着望远镜的小人，在每一个state处都可以看到未来一些时刻的事情。

看到了之后，我们会更新当前state，然后我们来到了下一个state，就不需要之前的states啦！future states会被不断观测和改变。

三、TD($\lambda$)

TD($\lambda$) 是强化学习中最古老且应用最广泛的算法，也是第一个阐述了forward-view 和backward-view间联系的算法（It was the first algorithm for which a formal relationship was shown between a more theoretical forward view and a more computationally congenial backward view using eligibility traces.）本节我们将介绍如何逼近上一小节提到的 off-line $\lambda$-return algorithm。

TD($\lambda$)对off-line ($\lambda$)-return算法进行了三点提升：

• 单步更新权重向量，无需等到episode结束，学习更快
• 计算在时间上均匀分布
• 不仅可用于episode问题，还适用于连续问题

本节介绍semi-gradient version of TD($\lambda$) with function approximation。在函数逼近时，eligiblility trace $z_t \in R^d$和权重向量$w_t$的元素个数相同，但权重向量有长期记忆，存在时间和系统等长，$z_t$是短期记忆，存在时间小于一个episode长度。eligiblility trace存在于学习过程中，their only consequence is that they affect the weight vector, and then the weight vector determines the estimated value。

在TD($\lambda$) 中，eligiblility trace vector 在episode开始时初始化为0，每个time step 由value梯度更新，且以$\gamma\lambda$衰减：

$\gamma$是discount rate,eligiblility trace一直追踪那些对recent state valuation有贡献的权重向量。这里 recent 是以$\gamma\lambda$界定的。回忆线性函数逼近，$\nabla \hat v(S_t \mathbf,w_t)$是特征向量$\mathbf x_t$，于是eligiblility trace vector只是所有过去衰减的输入向量和。trace暗示了当reinforcing event出现时的权重向量元素的重要程度，reinforcing event只得是one-step TD errors。state-value prediction的TD error为

在TD($\lambda$)中，权重更新公式为

算法伪代码如下:

TD($\lambda$)是backward in time的，即每个时刻，我们由当前TD error，按照对当前eligiblility trace的贡献程度，将其分配给之前的states。可以想象我们是一个拿着话筒的小人。沿着state 流计算 TD error，然后对之前经过的state 回喊。

有了TD error和trace，根据式（12.7）可以进行更新，当这些过去经历的states再次出现时更新他们的state value。

为了更好的理解backward view，从