An Analysis of Temporal-Difference Learning with Function Approximation

An Analysis of Temporal-Difference Learning with Function Approximation

II. DEFINITION OF TEMPORAL-DIFFERENCE LEARNING

论文
在这一节中，我们精确地定义了时间差分学习的性质，并将其应用于infinite-horizon discounted马尔科夫链的成本–目标函数的近似。虽然该方法适用于具有无限状态空间的马尔科夫链，但我们将注意力限制在状态空间是可数的情况下。这使我们能够使用相对简单的符号；例如，马尔科夫链可以用（无限的）转移概率矩阵来定义，而不是用转移概率核。扩展到一般状态空间的情况下，需要将矩阵符号转化为算子符号，但在其他方面是很简单的。

我们考虑一个 irreducible aperiodic马尔科夫链，其状态位于一个有限或无限空间$\mathbf{S}$中。通过用正整数对状态进行索引，我们可以把状态空间看作一个集合 S = { 1 , . . . , n } S=\{1,...,n\} S={1,...,n}，其中n可能是无限的。请注意，正整数在这里只是作为索引的作用。特别是，每个状态实际上可能对应于其他一些实体，比如描述物理系统状态的实数向量。在这种情况下，实际的状态空间将由欧氏空间的一个可数子集组成。

马尔可夫链访问的状态序列表示为 { i t ∣ t = 0 , 1 , . . . } \{i_t|t=0,1,...\} {it​∣t=0,1,...}。马尔科夫链的动态过程由一个（有限或无限）转移概率矩阵P来描述，其中$p_{i,j}$代表由状态i转换为状态j的概率($j=i_{t+1}$)。标量$g(i,j)$代表从i转移为j的代价(cost)。$\alpha \in (0,1)$是折扣因子。

关于cost-to-go函数（暂且把它称为值函数，以下值函数即代表cost-to-go函数）$J^{\ast }:S\to \mathcal{R}$的马尔科夫链定义为：

假设这个期望是定义良好的(assuming that this expectation is well-defined)。将$J$看作一个向量而不是一个函数(如果是无穷大，则其维数为无穷大)。

我们用一个函数逼近器$\tilde{J}:S\times {\mathcal{R}}^K\to \mathcal{R}$来近似$J^{\ast }:S\to \mathcal{R}$。为了近似值函数，人们通常会选择一个参数向量$r\in {\mathcal{R}}^K$，以使函数$\tilde{J}(\cdot ,r)and{J}^{\ast }(\cdot )$之间的误差最小。

假设我们观察到一串根据转移概率矩阵P生成的状态$i_t$，t时刻，参数向量r的值为$r_t$。我们定义了由$i_t$到$i_{t+1}$转移对应的时间差分$d_t$

对于$t=0,1,...,$，时间差分学习方法根据以下公式更新$r_t$：

$r_0$为随机初始化向量，${\gamma }_t$为一系列的步长标量，$\lambda \in [0,1]$，向量$\nabla \tilde{J}(i,r)$是关于r的偏导数。由于时间差分学习实际上是一个连续的算法，参数为$\lambda$，它通常被称为TD($\lambda$)。

在线性函数逼近器的特殊情况下，函数$\tilde{J}$采用这种形式

$r=(r(1),...,r(K))$为参数向量，每一个${\varphi }_k$是定义在状态空间S里的固定的标量函数(fixed scalar function)。${\varphi }_k$可以看成是基函数(basis functions) (或者是维度为|S|的向量 )，每一个$r(k)$可以看作是相关的权重。

用${\varphi }^{\prime }(i)=({\varphi }_1(i),...,{\varphi }_K(i))$来定义vector-valued function向量值函数$\varphi :S\to {\mathcal{R}}^K$。有了这个符号，近似值也可以写成这样的形式

$\Phi$可以被看成是一个$|S|\times K$的矩阵，第k列等于${\varphi }_k$

注意这里的梯度向量是

其中$\nabla \tilde{J}(r)$是雅可比矩阵，第i列为$\nabla \tilde{J}(i,r)$。

对于线性函数逼近器，通过定义维数为K的eligibility vectors资格向量序列，得到TD($\lambda$)更一般的表示

使用这种新符号，TD($\lambda$)更新由

资格向量可根据下式更新

初始化$z_{-1}=0$

在接下来的几节中，我们将重点讨论与线性函数逼近器一起使用的时间差学习。只有在第X节中，我们才回到非线性函数逼近器的更一般的背景。

III. UNDERSTANDING TEMPORAL-DIFFERENCE LEARNING

时差学习起源于强化学习领域。在最初的设定中，通常采用的观点是，该算法涉及 “回顾过去，纠正以前的预测”。在这种情况下，资格向量跟踪参数向量应该如何调整，以便在观察到时间差分$d_t$时适当地修改先前的预测。在本文中，我们采取了一种不同的观点，即研究算法的 "steady-state "行为，并认为这表征了参数向量的长期演变。在本节的其余部分，我们介绍了TD($\lambda$)，并在线性函数逼近器的背景下提供了它所导致的分析概述。我们的目标是传达一些关于算法如何工作的直觉，本着这种精神，我们将讨论保持在一个非正式的水平上，省略了技术假设和其他需要正式证明我们的statements的细节。这些技术性问题将在随后的章节中讨论，在这些章节中会提出正式的证明。

A. Inner Product Space Concepts and Notation

我们首先介绍一些符号，这些符号将使我们在这里的讨论以及本文后面的分析更加简洁。设$\pi (1),...,\pi (n)$表示过程$i_t$的平稳概率。我们假设对于$i\in S,\pi (i)>0$。定义D为对角线为$\pi (1),...,\pi (n)$的$n\times n$对角矩阵。很容易看出满足了内积的要求(satisfies the requirements for an inner product)。用$||\cdot |{|}_D=\sqrt{<\cdot ,\cdot {>}_D}$表示相关内积空间上的范数，向量的集合 { J ∈ R n ∣   ∣ ∣ J ∣ ∣ D < ∞ } \{J\in\mathcal R^n|\ ||J||_D<\infin\} {J∈Rn∣ ∣∣J∣∣D​<∞}用$L_2(S,D)$表示。后面我们会证明$J^{\ast }$ lies in $L_2(S,D)$。关于符号，我们也将继续使用$||\cdot ||$，不加下标，来表示有限维向量上的欧几里得范数或有限矩阵上的Euclidean-induced norm。(也就是是，对应矩阵A，我们有$||A||=ma{x}_{||x||=1}||Ax||$)。

我们假设每个基函数（basis function）${\varphi }_k$是$L_2(S,D)$的一个元素，所有 { Φ r ∣ r ∈ R K } ⊂ L 2 ( S , D ) \{\Phi r|r\in\mathcal R^K\}\subset L_2(S,D) {Φr∣r∈RK}⊂L2​(S,D)。对于每一对函数$J,\overline{J}\in L_2(S,D)$，当且仅当$⟨J,\overline{J}{⟩}_D=0$时，我们称J D-正交(D-orthogonal)$\overline{J}$，表示为$J{\perp }_D\overline{J}$。对于任意$J\in L_2(S,D)$，只存在唯一 J ‾ ∈ { Φ r ∗ ∣ r ∈ R K } \overline J\in\{\Phi r^*|r\in\mathcal R^K\} J∈{Φr∗∣r∈RK}使$||J-\overline{J}||$最小化。$\overline{J}$称为J在 { Φ r ∣ r ∈ R K } \{\Phi r|r\in\mathcal R^K\} {Φr∣r∈RK}上关于$⟨\cdot ,\cdot ⟩$的投影（This $\overline{J}$ is referred to as the projection of J on { Φ r ∣ r ∈ R K } \{\Phi r|r\in\mathcal R^K\} {Φr∣r∈RK} with respect to $⟨\cdot ,\cdot ⟩$）。我们定义一个“投影矩阵”$\Pi$(更准确地说，是投影算子)，应用于J已得到$\overline{J}$。假说basis functions基函数${\varphi }_1,...,{\varphi }_K$是线性无关的，投影矩阵为：

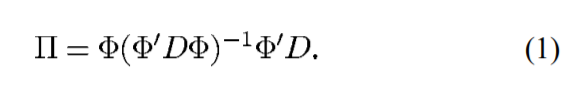
（注意${\Phi }^{\prime }D\Phi$是$K\times K$的矩阵）。对于所有$J\in L_2(S,D)$,我们有：


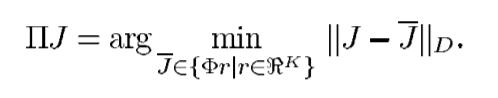
在给定一组固定的基函数时，投影$\Pi J^{\ast }$是$J^{\ast }$的一种自然的近似值（ a natural approximation）。 特别是，$\Pi J^{\ast }$是加权线性最小二乘法问题的解，即最小化

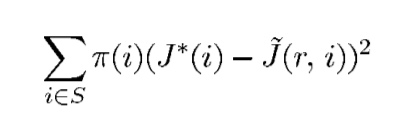
请注意，与每个状态相关的误差是由该状态被访问的频率来加权的。（如果状态空间是连续的而不是可计算的，这个和就会被一个积分所取代）。

B. The TD($\lambda$) Operator

为了简化我们对TD($\lambda$)的分析，我们引入了一个算子。这个算子，我们将其称为TD($\lambda$)操作符，由一个参数$\lambda \in [0,1]$索引(is indexed by a parameter$\lambda \in [0,1]$)并表示为$T^{(\lambda )}:L_2(S,D)\to L_2(S,D)$。它的定义是：

当$\lambda =1$时，极限为$li{m}_{\lambda \uparrow 1}(T^{(\lambda )}J)(i)=(T^{(1)}J)(i)$(under some technical conditions). 为了以有意义的方式解释TD($\lambda$)算子，请注意，对于每一个m，

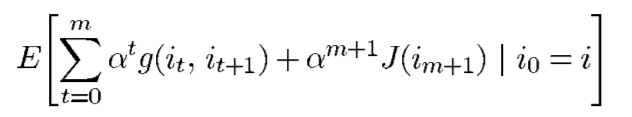
是在m个transitions内的expected cost，加上根据J计算出的remaining cost的近似值。这个总和有时被称为“m-stage truncated cost-to-go.”。直观地说，如果J是cost-to-go function的近似值，那么m-stage truncated cost-to-go可以看作是一种改进的近似值。由于$T^{(\lambda )}J$是在m-stage truncated cost-to-go上的加权平均，$T^{(\lambda )}J$也可以看作是一种改进的近似。 事实上，我们将在后面证明，$T^{(\lambda )}$是$L_2(S,D)$上的一个contraction ($T^{(\lambda )}$ is a contraction on $L_2(S,D)$)，它的不动点是$J^{\ast }$。因此， in the sense of the norm $||\cdot |{|}_D$，$T^{(\lambda )}J$总是比$J^{\ast }$实际更接近J。

C. Dynamics of the Algorithm

为了阐明TD($\lambda$)的基本结构，我们构造了一个过程$X_t=(i_t,i_{t+1},z_t)$。显然，$X_t$是一个马尔科夫过程。特别地，$z_{t+1}$和$i_{t+1}$是$X_t$的确定性函数，$i_{t+2}$的分布只依赖于$i_{t+1}$。请注意，在每个时间t，随机向量$X_t$与当前参数向量$r_t$一起，提供了计算$r_{t+1}$的所有必要信息。通过定义一个函数s

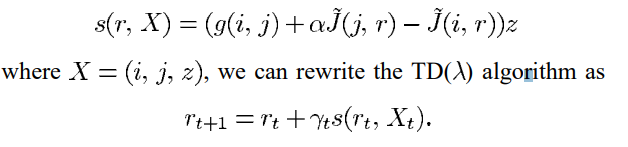
正如我们稍后将表明的那样，对于任何r，$s(r,X_t)$都有一个well-defined “steady-state” expectation，我们用$E_0[s(r,X_t)]$表示。直观地说，一旦$X_t$达到稳定状态，TD($\lambda$)算法在 "平均 "的意义上，表现得像下面的确定性算法。

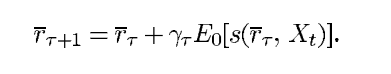
在一些技术假设下，这种确定性算法的收敛性意味着TD($\lambda$)的收敛性，而且两种算法都有相同的收敛极限。我们的研究集中在对这种确定性算法的分析上。