LIF模型简介

脉冲神经网络中LIF模型简介

文章借鉴电子书Neuronal Dynamics

LIF模型 Integrate-And-Fire Models

  神经元动力学：被认为是一个求和（“整合”）过程，我们用一个正式的阈值$\vartheta$来描述脉冲起始的临界电压。如果电压$u_i(t)$(包含所有输入的总和)从最底到达阈值$\vartheta$，我们说神经元$i$发出一个脉冲。阈值越过的时刻定义了触发时间$t_i^{(f)}$。
  该模型利用了一个事实，即给定神经元的神经元动作电位总是具有大致相同的形式。如果动作电位的形状总是相同的，那么该形状就不能用来传递信息：相反，信息包含在有无脉冲中。因此，动作电位被降低为在某个精确时刻发生的“事件”。
  Integrate-and-Fire 模型由两个独立部分组成，这两部分都是模型所必须的，第一，一个描述膜电位$u_i(t)$的演化方程；第二，产生脉冲的机制。
"发射时间 "是指一个特定的神经元发出动作电位$t^{(f)}$的时刻。漏积分-发射模型中的发射时间$t^{(f)}$由阈值准则$t^{(f)}$定义：$u(t^f)=\vartheta$。
脉冲峰值的形式没有被明确描述。而是注意到发射时间，并在$t^{(f)}$之后立即将电位重置为新值$u{}_r<\vartheta$。$$\underset{\delta \mapsto 0;\delta >0}{\lim }u(t^{(f)}+\delta )=u_r$$
对于神经元$i$的发射时间，我们写$t_i^{(f)}$，其中f=1,2,…是脉冲的标签。从形式上看，我们可以把一个神经元$i$的脉冲序列表示为发射时间的序列:$$s_i(t)=\sum _f\delta (t-t_i^{(f)})$$
其中δ(x)是前面介绍的狄拉克$\delta$函数，$\delta (x)=0$，$x\ne 0$,${\int }_{-\infty }^{+\infty }\delta (x)=1$。因此，脉冲被简化为时间上的点（图1.8）

图1.8:在脉冲神经元的正式模型中，动作电位(虚线)的形状通常被$\delta$脉冲(垂直线)所代替。脉冲后的负超调(峰后电位)被膜电位的“重置”值$u_r$所取代。脉冲由阈值在$t_i^{(1)}$处触发。

（1）膜电位演化的线性微分方程

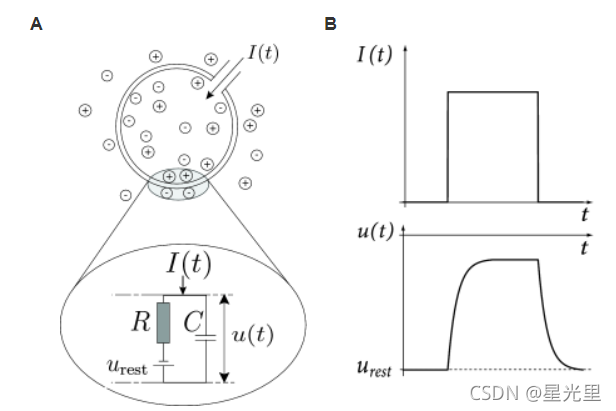
  变量$u_i$描述了神经元$i$的膜电位的瞬时值。在没有任何输入的情况下，电位处于其静息值$u_{rest}$。如果实验人员向神经元注入电流$I(t)$，或者如果神经元接受来自其他神经元的突触输入，潜在的$u_i$将偏离其静息值。
  为了得到瞬时电压$u_i(t)-u_{rest}$与输入电流$I(t)$之间的联系方程，通过电学理论中的基本定律。神经元被细胞膜包围，细胞膜是一种很好的绝缘体。如果一个短电流脉冲I(t)被注入神经元，额外的电荷$q=\int I(t^{\prime })d{t}^{\prime }$必须到达某个地方:它将向细胞膜充电(图A)。因此，细胞膜就像一个容量为$C$的电容器。因为绝缘体并不完美，电荷会随着时间的推移慢慢地通过细胞膜。因此，细胞膜可以用有限的防漏系数$R$来表征。
  用基本电路表示来LIF模型，包括电容器C与电阻R并联，由电流$I(t)$驱动;见图上。
  如果驱动电流$I(t)$消失，通过电容器的电压由电池电压$u_{rest}$提供。
  分析电路：运用电流守恒定律：$I(t)=I_R+I_C$
其中，$I_R$是通过电阻R的电流，根据欧姆定律$I_R=u_R/R$，其中$u_R=u-u_{rest}$是通过电阻的电压，$I_C$是给电容器C充电。由电容C=q/u(其中q是电荷，u是电压)的定义，可以得到电容电流$I_C=dq/dt=C\frac{du}{dt}$。因此:
将Eq.(1.4)乘以R，并引入时间常数τm=RC。这就产生了标准形式:

我们称$u$为膜电位，${\tau }_m$为神经元的膜时间常数。
从数学的角度来看，Eq.(1.5)是一个线性微分方程。从电气工程师的角度来看，它是一个漏泄的积分器(leaky integrator)或 RC 电路，其中电阻R和电容C并联。从神经学家的观点来看，式(1.5)称为被动膜方程。Eq.(1.5)的解是什么?假设，无论出于什么原因，在t=0时，膜电势的值为$u_{rest}+\Delta u$。对于$t>0$，输入为$I(t)=0$。我们直觉地认为，如果我们等待的时间足够长，膜电位就会降低到它的静息值$u_{rest}$。确实，初始条件为$u(t0)=u_{rest}+\Delta u$的微分方程的解为:
解(1.6)的有效性可以通过对方程两边求导来验证。因为它是在没有输入的情况下的解，所以它有时被称为“自由”解。

  在一个简单的例子中研究Eq.(1.5)定义的被动膜的动力学。假设被动膜受到恒定的输入电流$I(t)=I_0$的刺激，该电流从$t=0$开始，结束于时间$t=\Delta$。为了简便起见，我们假设$t=0$时的膜电位处于其静息值,即初始条件：$u(0)=u_{rest}$。
$0<t<\Delta$的解：
  如果输入电流不停止，则膜电位(1.7)在$t\to \infty$时趋近于u(∞)的渐近值 $u(\infty )=u_{rest}+R{I}_0$。可以通过查看图1.6中RC电路的电路图来理解这个结果。一旦达到稳定状态，电容上的电荷就不再改变。所有的输入电流必须通过电阻器。因此，电阻处的稳态电压为$R{I}_0$，因此总膜电压为$u_{rest}+R{I}_0$。

欧拉方法解Eq.(1.5)的微分方程：

$\frac{du}{dt}=u(t+1)-u(t)$，
对于Eq.(1.5)来说：运用欧拉方法解该线性方程：
$u(t)=(1-\frac{1}{{\tau }_m})u(t-1)+\frac{1}{{\tau }_m}{u}_{rest}+\frac{RI(t)}{{\tau }_m}$