齐次坐标的含义

齐次坐标点的表示：

why：有了笛卡尔坐标，我为什么还要使用齐次坐标呢？
在做旋转和缩放的时候，如果采用笛卡尔坐标的话，可以直接乘以旋转角度和缩放尺度就可以对图片进行处理，但是如果做平移变换的时候，笛卡尔坐标无法满足直接在坐标点做矩阵的相乘运算，但是引入笛卡尔坐标的话就能够很好的解决这个问题。

旋转变换：

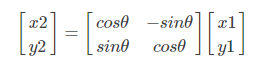
缩放变换

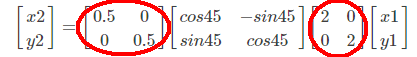
平移变换
使用笛卡尔坐标的时候不能够像旋转缩放那样很漂亮的进行数学计算，但是引入齐次坐标就能够很漂亮的解决这个问题：

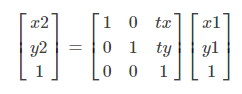
有了齐次坐标的使用，终于可以统一预算了。以后所有的变换，不管怎样变换，变换多少次，都可以表示成一连串的矩阵相乘了，这是多么的方便。这就是引入齐次坐标的作用，把各种变换都统一了起来。

how：那么如何将笛卡尔坐标转换成齐次坐标呢
既然这么方便，那么如何将笛卡尔坐标转换成齐次坐标呢？
齐次坐标
简而言之，齐次坐标就是用N+1维来代表N维坐标。我们可以在一个2D笛卡尔坐标末尾加上一个额外的变量w来形成2D齐次坐标，因此，一个点(X,Y)在齐次坐标里面变成了（x,y,w），并且一定有：
X = x/w
Y = y/w
也就是说我们把齐次坐标转化为笛卡尔坐标的方法是前面n-1个坐标分量分别除以最后一个分量即可。

在转换的过程中，会发现(1, 2, 3), (2, 4, 6) 和(4, 8, 12)对应同一个笛卡尔坐标点 (1/3, 2/3)，任何标量的乘积，例如(1a, 2a, 3a) 对应 笛卡尔空间里面的(1/3, 2/3) 。因此，这些点是“齐次的”，因为他们代表了笛卡尔坐标系里面的同一个点。换句话说，齐次坐标有规模不变性。

另外需要提一点的是，如何证明无穷远点可以有平行线相交的证明：