METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS 翻译（二）

METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS（二）

2. 下降方法

所有非线性优化的方法都基于是迭代的。从一个起点 ${x\text{x}x}_0$开始，该方法产生一系列的向量 ${x\text{x}x}_1,{x\text{x}x}_2,...,$（希望能） 收敛到 ${x\text{x}x}^{\ast }$ ，即给定函数的局部最小值，见定义1.3.。大多数方法都有强制执行下降条件的措施
$$F({x\text{x}x}_{k+1})<F({x\text{x}x}_k)\text{\hspace{1em}(2.1)}$$

这可以防止收敛到最大值，也使我们收敛到鞍点的概率降低。如果给定的函数有几个最小值，其结果将取决于起始点 ${x\text{x}x}_0$。我们不知道哪一个最小值将被发现；它不一定是最接近 ${x\text{x}x}_0$ 的最小值。

在许多情况下，该方法产生的向量会在两个明显不同的阶段向最小值收敛。当 ${x\text{x}x}_0$ 离解很远时 我们希望该方法产生的迭代结果能稳定地朝向 ${x\text{x}x}^{\ast }$ 移动。在这个迭代的 “全局阶段”，除非是在最初的步骤中， 如果误差不增加，我们就满意了。即
$$||{e\text{e}e}_{k+1}||<||{e\text{e}e}_k||fork>K$$

其中 ${e\text{e}e}_k$ 表示当前的误差，
$${e\text{e}e}_k={x\text{x}x}_k-{x\text{x}x}^{\ast }\text{\hspace{1em}(2.2)}$$

在迭代的最后阶段，即当 ${x\text{x}x}_k$ 接近 ${x\text{x}x}^{\ast }$ 时，我们希望更快的收敛。我们对以下情况进行区分

• 线性收敛：
  $$||{e\text{e}e}_{k+1}||\le a||{e\text{e}e}_k||when||{e\text{e}e}_k||issmall;0<a<1,\text{\hspace{1em}(2.3a)}$$
• 二次收敛：
  $$||{e\text{e}e}_{k+1}||=O(||{e\text{e}e}_k|{|}^2)when||e_k||issmall\text{\hspace{1em}(2.3b)}$$
• 超线性收敛：
  $$||{e\text{e}e}_{k+1}||/||{e\text{e}e}_k||\to 0fork\to \infty \text{\hspace{1em}(2.3c)}$$

本讲义中介绍的方法是在迭代的每一步都满足下降条件（2.1）的下降方法。当前迭代的一步包括

1. 找到一个下降方向 ${h\text{h}h}_d$（在下面讨论），并且
2. 找到一个能很好地减少 $F$ 值的步长。

因此，一个下降方法的概要是

考虑 $F$ 值沿着以 $x\text{x}x$ 为起点，以 $h\text{h}h$ 为方向的的直线的变化情况。从泰勒展开（1.4a）中我们可以看到
$$\begin{gathered} F(x\text{x}x+\alpha h\text{h}h)=F(x\text{x}x)+\alpha {h\text{h}h}^T\dot{F}(x\text{x}x)+O({\alpha }^2) \\ \approx F(x\text{x}x)+\alpha {h\text{h}h}^T\dot{F}(x\text{x}x)for\alpha sufficientlysmall\text{\hspace{1em}(2.5)} \end{gathered}$$

如果 $F(x\text{x}x+\alpha h\text{h}h)$ 在 $\alpha =1$ 时是关于 $\alpha$ 的递减函数，我们就说 $h\text{h}h$ 是一个下降方向。 这引出了以下定义。

定义2.6. 下降方向

如果 ${h\text{h}h}^{T}F(x\text{x}x)<0$，则 $h\text{h}h$ 是 $F$ 在 $x\text{x}x$ 处的下降方向。

如果不存在这样的 $h\text{h}h$，则 $\dot{F}(x\text{x}x)=0$，表明在这种情况下 $x\text{x}x$ 是驻点。否则，我们必须选择$\alpha$，即我们应该在 ${h\text{h}h}_d$ 给定的方向上从 $x\text{x}x$ 出发移动多远，以便得到目标函数值的减少。这样做的一个方法是找到（一个近似值）
α e = a r g m i n α > 0 { F ( x + α h ) } (2.7) \alpha_e = argmin_{\alpha > 0}\{F(\pmb{x}+\alpha \pmb{h})\} \tag{2.7} αe​=argminα>0​{F(xxx+αhhh)}(2.7)

这个过程被称为线搜索，并将在第 2.3 节中讨论。然而，首先我们将介绍两种计算下降方向的方法。

2.1 最陡峭的下降方法

从（2.5）中我们可以看出，当我们执行一个具有正的 $\alpha$ 值的步长 $\alpha h\text{h}h$ 时，那么 目标函数值的相对增益满足
$$\underset{\alpha \to 0}{\lim }\frac{F(x\text{x}x)-F(x\text{x}x+\alpha h\text{h}h)}{\alpha ||h\text{h}h||}=-\frac{1}{||h\text{h}h||}{h\text{h}h}^T\dot{F}(x\text{x}x)=-||\dot{F}(x\text{x}x)||cos\theta$$

其中 $\theta$ 是向量 $h\text{h}h$ 和 $\dot{F}(x\text{x}x)$ 之间的角度。这表明，如果 $\theta =0$，即如果我们使用由下式给出的最陡峭的下降方向 ${h\text{h}h}_{sd}$，我们可以得到最大的增益率
$${h\text{h}h}_{sd}=-\dot{F}(x\text{x}x)\text{\hspace{1em}(2.8)}$$

基于（2.8）的方法（即算法2.4中的 ${h\text{h}h}_d={h\text{h}h}_{sd}$）被称为最陡峭下降法或梯度法。下降方向的选择是 “最好的”（局部），我们可以将其与精确的线搜索（2.7）相结合。像这样的方法会收敛，但最终的收敛性能是线性的，而且往往很慢。Frandsen et al (2004) 中的例子显示了使用精确的线搜索的最陡峭下降法在有限的计算机精度的情况下可能无法找到二阶多项式的最小化值。然而，对于许多问题。该方法在迭代过程的初始阶段具有相当好的性能。

诸如此类的考虑导致了所谓的混合方法，顾名思义，是基于两种不同的方法。一种是在初始阶段很好的，比如梯度法，而另一种方法则在最后阶段很好，比如牛顿法（见下一节）。混合方法的一个主要问题是找到在两种方法之间进行适当切换的机制。

2.2 牛顿法

我们可以从 $x^{\ast }$ 是一个驻点的条件推导出这种方法。根据定义1.6，它满足 $\dot{F}({x\text{x}x}^{\ast })=0$。这是一个非线性方程组，根据泰勒展开
$$\begin{gathered} \dot{F}(x\text{x}x+h\text{h}h)=\dot{F}(x\text{x}x)+\ddot{F}(x\text{x}x)h\text{h}h+O(||h\text{h}h|{|}^2) \\ \approx \dot{F}(x\text{x}x)+\ddot{F}(x\text{x}x)h\text{h}hfor||h\text{h}h||sufficientlysmall \end{gathered}$$

我们推导出牛顿法。找出 ${h\text{h}h}_n$ 的作为以下方程的解
$$H\text{H}H{h\text{h}h}_n=-\dot{F}(x\text{x}x)withH\text{H}H=\ddot{F}(x\text{x}x)\text{\hspace{1em}(2.9a)}$$

并通过以下方式计算下一次迭代
$$x\text{x}x:=x\text{x}x+{h\text{h}h}_n\text{\hspace{1em}(2.9b)}$$

假设 $H\text{H}H$ 是正定的，那么它就是非奇异的（意味着（2.9a）有一个唯一的解），并且对于所有非零的 $u\text{u}u$，都满足 ${u\text{u}u}^{T}H\text{H}Hu\text{u}u>0$。 因此在（2.9a）的两边都乘以 ${h\text{h}h}_n^T$，我们得到
$$0<{h\text{h}h}_n^{T}H\text{H}H{h\text{h}h}_n=-{h\text{h}h}_n\dot{F}(x\text{x}x)\text{\hspace{1em}(2.10)}$$

这个公式表明 $h_n$ 是一个下降方向：它满足定义 2.6 的条件。

牛顿法在迭代的最后阶段的性能非常好，此时 $x\text{x}x$ 接近于${x\text{x}x}^{\ast }$。我们可以证明（见 Frandsen等人(2004) ），如果海塞矩阵在 ${x\text{x}x}^{\ast }$ 处是正定的（满足定理1.8中的充分条件），并且我们在 ${x\text{x}x}^{\ast }$ 周围的 $\ddot{F}(x\text{x}x)$ 是正定的区域内，则我们会得到二次收敛（定义见（2.3）)。 另一方面，如果 $x\text{x}x$ 位于 $\ddot{F}(x\text{x}x)$ 为负定的区域内，并且那里有一个驻点，基础的牛顿方法（2.9）将向这个为最大值的驻点收敛（二次）。 我们可以通过要求所有的步骤都在下降方向来避免这种情况

我们可以建立一个混合方法，基于牛顿法和最速下降法。根据（2.10），如果 $\ddot{F}(x\text{x}x)$ 是正定的，则​​牛顿步长保证代价函数是下降的，所以这个混合算法的中心部分的概述可以是
$$\begin{array}{cc}if\ddot{F}(x\text{x}x)ispositivedefinite& \\ h\text{h}h:={h\text{h}h}_n& \\ else& \\ h\text{h}h:={h\text{h}h}_{sd}& \\ x\text{x}x:=x\text{x}x+\alpha h\text{h}h& \end{array}\text{\hspace{1em}(2.11)}$$

这里，${h\text{h}h}_{sd}$ 是最陡峭的下降方向，$\alpha$ 是通过线搜索找到的（见第2.3节）。检查矩阵的正定性的一个好工具是 Cholesky 方法（见附录A），当该方法成功时，也可用求解问题中的线性系统。因此，对正定性的检查是几乎是免费的。

在第2.4节中，我们介绍了一些方法，其中搜索方向 ${h\text{h}h}_d$ 和步长 $\alpha$ 的计算是同时进行的。并给出了一个没有线搜索的（2.11）的版本。这样的混合方法可能非常有效，但它们几乎没有被使用过。原因是它们需要 $\ddot{F}(x)\text{x)}x)$ 的实现，而对于复杂的应用问题，这是不可能的。相反，我们可以使用一个所谓的准牛顿方法，它基于逐渐逼近 ${H\text{H}H}^{\ast }=\ddot{F}({x\text{x}x}^{\ast })$ 的一系列矩阵。在第3.4节我们介绍了这样的一种方法。也可以参考 Frandsen et al (2004) 的第5章。

2.3 线搜索

给定一个点 $x\text{x}x$ 和一个下降方向 $h\text{h}h$。下一个迭代步骤是从 $x\text{x}x$ 出发向 $h\text{h}h$ 方向移动。为了找出该移动多远，我们研究了给定的函数沿着 从$x\text{x}x$ 出发沿着 $h\text{h}h$ 方向的直线的变化，
$$\phi (\alpha )=F(x\text{x}x+\alpha h\text{h}h),x\text{x}xandh\text{h}hfixed,\alpha \ge 0\text{\hspace{1em}(2.12)}$$

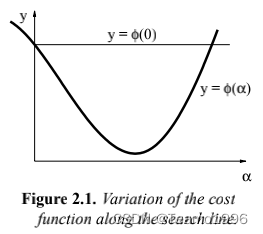
图2.1显示了 $\phi (\alpha )$ 的函数示例。

我们的 $h\text{h}h$ 是一个下降方向，确保了
$$\dot{\phi }(0)={h\text{h}h}^T\dot{F}(x\text{x}x)<0$$

这表明如果 $\alpha$ 足够小，我们满足下降条件（2.1），它等价于
$$\phi (\alpha )<\phi (0)$$

通常，我们会对 $\alpha$ 给一个初始猜测值，例如使用牛顿法的 $\alpha =1$。图2.1说明了可能会出现的三种不同的情况

1. $\alpha$ 非常小，目标函数的值增益非常小。$\alpha$ 应该被增加。
2. $\alpha$太大了：$\phi (\alpha )\ge \phi (0)$。应该降低 $\alpha$ 以满足下降条件（2.1）。
3. $\alpha$ 接近于$\phi (\alpha )$ 的最小值。接受此 $\alpha$ 值。

   更准确地说，是：$\phi$ 的最小的局部最小值。如果我们将 $\alpha$ 增加到超过图 2.1 所示的区间之外，那么我们很可能会接近 $F$ 的另一个局部最小值。

精确的线搜索是一个迭代过程，产生一系列 ${\alpha }_1,{\alpha }_2,...$。目的是找到（2.7）中定义的真正的最小值 ${\alpha }_e$，当迭代 ${\alpha }_s$ 满足以下条件时，算法停止
$$|\dot{\phi ({\alpha }_s)}|\le \tau |\dot{\phi (0)}|$$

其中 $\tau$ 是一个很小的正数。在迭代中，我们可以使用基于以下的计算值的 $\phi (\alpha )$ 的变化的近似
$$\phi ({\alpha }_k)=F(x\text{x}x+{\alpha }_{k}h\text{h}h)and\dot{\phi ({\alpha }_k)}={h\text{h}h}^T\dot{F\text{F}F}(x\text{x}x+{\alpha }_{k}h\text{h}h)$$

详见 Frandsen et al (2004) 的第2.5-2.6节。

精确的线搜索可能会浪费大量的计算时间：当 $x\text{x}x$ 远离 ${x\text{x}x}^{\ast }$ 时，搜索方向 $h\text{h}h$ 可能远离方向 ${x\text{x}x}^{\ast }-x\text{x}x$，并且不需要非常准确地找到 $\phi$ 的真实的最小值。这是所谓的软线搜索的背景，当 $\alpha$ 的值不属于上面列出的类别1或2，我们就接受这个 $\alpha$ 值。我们使用下降条件（2.1）的更严格的版本，即
$$\phi ({\alpha }_s)\le \phi (0)+{\gamma }_1\cdot \dot{\phi }(0)with0<{\gamma }_1<1\text{\hspace{1em}(2.13a)}$$

这确保了我们不在类别2中。类别1对应于点 $(\alpha ,\phi (\alpha ))$ 太接近起始切线，我们用以下条件进行补充
$$\dot{\phi }({\alpha }_s)\ge {\gamma }_2\cdot \dot{\phi }(0)with{\gamma }_1<{\gamma }_2<1\text{\hspace{1em}(2.13b)}$$

注意：这里的$\dot{\phi }$是负数

如果对 $\alpha$ 的初始猜测值满足这两个准则，那么我们接受它作为 ${\alpha }_s$。否则，我们必须使用对应的算法进行迭代，以进行精确的线搜索。详细信息见 Frandsen et al (2004) 的第2.5节。

2.4. 信赖域和阻尼方法

假设我们在当前迭代 $x\text{x}x$ 的附近有一个 $F$ 行为的模型 $L$，
$$F(x\text{x}x+h\text{h}h)\approx L(h\text{h}h)=F(x\text{x}x)+{h\text{h}h}^{T}c+\frac{1}{2}{h\text{h}h}^{T}B\text{B}Bh\text{h}h\text{\hspace{1em}(2.14)}$$

其中 $c\text{c}c\in {\mathbb{R}}^n$ 并且矩阵 $B\text{B}B\in {\mathbb{R}}^{n\times n}$ 是对称的。本节的基本思想可以推广到其他形式的模型，但在本手册中，我们只需要在（2.14）中给出的 $L$ 的形式。通常，该模型是 $F$ 在 $x\text{x}x$ 附近的二阶泰勒展开，就像公式（1.4a）的右边的前三项一样，或者 $L(h)$ 可能是这个展开的近似。一般来说，只有当 $h\text{h}h$ 足够小时，这个模型才是好的。我们将介绍两种包含这种思想的用于确定 $h\text{h}h$ 的方法，其中 $h\text{h}h$ 是一个下降方向，可以在算法 2.4 中当 $\alpha =1$ 的情况下使用。

在信赖域方法中，我们假设我们知道一个正数 $\Delta$，这样模型在半径为 $\Delta$、以 $x\text{x}x$ 为中心的球内足够精确，并确定步长为

h = h t r = a r g m i n ∣ ∣ h ∣ ∣ < Δ { L ( h ) } (2.15) \pmb{h} = \pmb{h}_{tr}=argmin_{||\pmb{h}||<\Delta}\{L(\pmb{h})\} \tag{2.15} hhh=hhhtr​=argmin∣∣hhh∣∣<Δ​{L(hhh)}(2.15)

在一种阻尼方法中，该步长由以下公式确定
h = h d m = a r g m i n h { L ( h ) + 1 2 μ h T h } (2.16) \pmb{h} = \pmb{h}_{dm} = argmin_{\pmb{h}} \{L(\pmb{h})+\frac{1}{2}\mu \pmb{h}^T\pmb{h}\} \tag{2.16} hhh=hhhdm​=argminhhh​{L(hhh)+21​μhhhThhh}(2.16)

其中，阻尼参数 $\mu \ge 0$。项 $\frac{1}{2}\mu {h\text{h}h}^{T}h\text{h}h=\frac{1}{2}\mu ||h\text{h}h|{|}^2$ 用于惩罚大的步长。

基于这些方法之一的算法 2.4 的核心部分具有以下形式
$$\begin{array}{c}Computehby(2.15)or(2.16)\\ ifF(x\text{x}x+h\text{h}h)<F(x\text{x}x)\\ x\text{x}x:=x\text{x}x+h\text{h}h\\ Update\Delta or\mu \end{array}\text{\hspace{1em}(2.17)}$$

如果步长 $h\text{h}h$ 满足下降条件（2.1），则这对应于 $\alpha =1$。否则，$\alpha =0$，即我们不移动。然而，我们并没有停留在 $x\text{x}x$ 上(除非 $x\text{x}x={x\text{x}x}^{\ast }$)：通过对 $\Delta$ 或 $\mu$ 的适当修改，我们的目标是在下一步迭代中获得更好的解。

这些方法有一些版本，它们包含适当的线搜索来找到具有较小 $F$ 值的点 $x\text{x}x+\alpha h\text{h}h$，以及在线搜索过程中收集的信息用于更新 $\Delta$ 或 $\mu$。对于许多问题，这样的版本使用更少的迭代步骤，但具有更大的累积下降的函数值。

由于假设 $L(h\text{h}h)$ 是当 $h\text{h}h$ 足够小时 $F(x\text{x}x+h\text{h}h)$ 的一个很好的近似，所以这个步骤失败的原因是 $h\text{h}h$ 太大了，应该被减少。此外，如果该步长被接受，则可以在新的迭代中使用更大的步长，从而减少在我们达到${x\text{x}x}^{\ast }$之前所需的迭代次数。

在之后的表述中针对 $\alpha h\text{h}h$ 和 $h\text{h}h$ 我们统一使用步长这一术语，不做区分，但根据上下文可以很容易明白具体的指代。

使用计算出来步长的模型的质量可以通过所谓的增益比来评估
$$\wp =\frac{F\text{F}F(x\text{x}x)-F(x\text{x}x+h\text{h}h)}{L(0)-L(h\text{h}h)}\text{\hspace{1em}(2.18)}$$

即函数值的实际下降和模型的预测下降之间的比率。通过构造，分母是正的，如果步长不是向下的，那么分子就是负的—它太大了，应该被减少。

在信赖域方法中，我们通过半径 $\Delta$ 的大小来控制步长。以下的更新策略被广泛使用，

i f   ℘ < 0.25 Δ : Δ / 2 e l s e i f   ℘ > 0.75 Δ : m a x { Δ , 3 ∗ ∣ ∣ h ∣ ∣ } (2.19) \begin{matrix} if \, \wp < 0.25 \\ \quad \quad \quad \Delta:\Delta/2 \\ elseif \, \wp >0.75 \\ \quad \quad \quad \quad \quad \quad \quad \quad \Delta:max\{\Delta,3 * ||\pmb{h}||\}\end{matrix} \tag{2.19} if℘<0.25Δ:Δ/2elseif℘>0.75Δ:max{Δ,3∗∣∣hhh∣∣}​(2.19)

因此，如果 $\wp <0.25$，则我们决定使用较小的步长，而 $\wp >0.75$ 则表示可以使用较大的步长。信赖域算法对阈值 $0.25$ 和 $0.75$、除数 $p_1=2$ 或因子 $p_2=3$ 的微小变化不敏感，但重要的是数字 $p_1$ 和 $p_2$ 的选择必须确保 $\Delta$ 值不能振荡。

而在阻尼法中，小的 $\wp$ 表示我们应该增加阻尼因子，从而增加大对大的步长的惩罚。较大的 $\wp$ 表示对于计算得到的$h\text{h}h$，$L(h\text{h}h)$ 是 $F(x\text{x}x+h\text{h}h)$ 的良好近似，并且阻尼参数可以减小。一种广泛使用的策略如下，它类似于（2.19），最初是由Marquardt（1963）提出的，

$$\begin{array}{c}if\wp <0.25\\ \mu :=\mu \ast 2\\ elseif\wp >0.75\\ \mu :=\mu /3\end{array}\text{\hspace{1em}(2.20)}$$

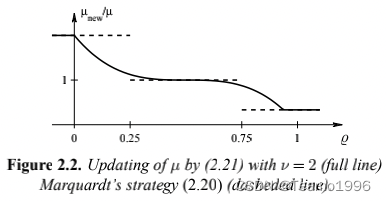
同样，该方法对阈值 $0.25$ 和 $0.75$ 或数字 $p_1=2$ 和 $p_2=3$ 的微小变化不敏感，但重要的数字 $p_1$ 和 $p_2$ 的选择必须确确保 $\mu$ 值不能振荡。经验表明，穿越阈值 $0.25$ 和 $0.75$ 时 $\mu$ 值的不连续变化会导致“颤振”（如例 3.7 所示），从而减慢收敛速度，我们在Nielsen（1999）中证明，以下策略总体上优于（2.20），

i f   ℘ > 0 μ : = μ ∗ m a x { 1 3 , 1 − ( 2 ℘ − 1 ) 3 } ; v : = 2 e l s e μ : = μ ∗ v ; v : = 2 ∗ v (2.21) \begin{matrix} if \, \wp > 0 \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \mu:=\mu*max\{\frac{1}{3},1-(2\wp -1)^3\}; \quad v:=2 \\ else\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \mu:= \mu*v; \quad v:=2*v\end{matrix} \tag{2.21} if℘>0μ:=μ∗max{31​,1−(2℘−1)3};v:=2elseμ:=μ∗v;v:=2∗v​(2.21)

因子 $\nu$ 被初始化为 $\nu =2$。请注意，一系列连续的失败结果会导致 $\mu$ 值的快速增加。这两个更新公式的行为如下图所示。

2.4.1. 步长的计算

在阻尼方法中，步长被计算为以下函数的一个驻点
$${\psi }_{\mu }(h\text{h}h)=L(h\text{h}h)+\frac{1}{2}\mu {h\text{h}h}^{T}h\text{h}h$$

这意味着 ${h\text{h}h}_{dm}$ 是以下方程的解

$${\dot{\psi }}_{\mu }(h\text{h}h)=\dot{L}(h\text{h}h)+\mu h\text{h}h=0$$

从（2.14）中的 $L(h\text{h}h)$ 的定义中我们可以看出，以上方程等价于
$$(B\text{B}B+\mu I\text{I}I){h\text{h}h}_{dm}=-c\text{\hspace{1em}(2.22)}$$

其中，$I\text{I}I$ 是单位矩阵。如果 $\mu$ 足够大，对称矩阵 $B\text{B}B+\mu I\text{I}I$ 是正定的（见附录A），然后从定理 1.8 得出，$h_{dm}$ 是 $L$ 的最小值。

示例 2.1.

在阻尼牛顿法中，模型 $L(h\text{h}h)$ 由 $c=\dot{F}(x\text{x}x)$ 和 $B=\ddot{F}(x\text{x}x)$ 给出，则（2.22）具有以下形式
$$(\ddot{F}(x\text{x}x)+\mu I\text{I}I){h\text{h}h}_{dn}=-\dot{F}(x\text{x}x)$$

$h_{dn}$ 是所谓的阻尼牛顿步长。如果 $\mu$ 很大，则
$${h\text{h}h}_{dn}\approx -\frac{1}{\mu }\dot{F}(x\text{x}x)$$

即向接近最陡下降方向走的一小步。另一方面，如果 $\mu$ 非常小，那么 ${h\text{h}h}_{dn}$ 就接近牛顿步长 ${h\text{h}h}_n$。因此，我们可以认为阻尼牛顿法是最陡下降法和牛顿法的混合方法。

我们在 3.2 节中重新回到阻尼方法。

在信赖域方法中，步长 ${h\text{h}h}_{tr}$ 是一个带约束优化问题的解，
$$\begin{array}{c}minimizeL(h\text{h}h)\\ subjectto{h\text{h}h}^{T}h\text{h}h\le {\Delta }^2\end{array}\text{\hspace{1em}(2.23)}$$

详细讨论这个问题不在本手册的范围之内（见 Madsen et al (2004) 或 Nocedal and Wright (1999) 的第4.1节）。我们只想提到一些属性。

如果（2.14）中的矩阵 $B\text{B}B$ 是正定的，则 $L$ 的无约束最小值是以下方程的解
$$B\text{B}Bh\text{h}h=-c\text{c}c$$

如果这足够小（如果它满足 ${h\text{h}h}^{T}h\text{h}h\le {\Delta }^2$），那么这是期望的步长 ${h\text{h}h}_{tr}$。否则，约束是被激活的的，问题就更加复杂。使用与我们在线搜索中使用的类似的论证，我们可以看到我们不需要计算（2.23）的真正解，并且在第 3.3 和 3.4 节中，我们提出了两种计算 ${h\text{h}h}_{tr}$ 近似解的方法。

最后，我们指出两个在 $B\text{B}B$ 是正定的情况下阻尼方法和信赖域法的相似之处：如果无约束最小值在信赖域之外，可以证明（Madsen et al (2004) 中的定理 2.11）存在一个 $\lambda >0$ 满足
$$B\text{B}B{h\text{h}h}_{tr}+c\text{c}c=-\lambda {h\text{h}h}_{tr}\text{\hspace{1em}(2.24 a)}$$

通过对该方程进行重新排列并与（2.22）进行比较，我们发现 ${h\text{h}h}_{tr}$ 与用阻尼参数 $\mu =\lambda$ 计算的阻尼步长 ${h\text{h}h}_{dm}$ 是相同的。另一方面，我们也可以证明（ Frandsen et al (2004) 中的定理 5.11 )，如果我们为给定的 $\mu \ge 0$ 计算 ${h\text{h}h}_{dm}$，那么
h d m = a r g m i n ∣ ∣ h ∣ ∣ ≤ ∣ ∣ h d m ∣ ∣ { L ( h ) } (2.24 b) \pmb{h}_{dm}=argmin_{||\pmb{h}|| \leq ||\pmb{h}_{dm}||} \{L(\pmb{h})\} \tag{2.24 b} hhhdm​=argmin∣∣hhh∣∣≤∣∣hhhdm​∣∣​{L(hhh)}(2.24 b)

也就是说 ${h\text{h}h}_{dm}$ 等于信赖域半径 $\Delta =||{h\text{h}h}_{dm}||$ 的 ${h\text{h}h}_{tr}$。因此，这两类方法是密切相关的，但是没有一个简单的公式来说明 $\Delta$ 值和 $\mu$ 值之间的关系，从而给出相同的步长。