opencv支持python3.7吗_（四十五）OpenCV中的机器学习-用SVM做图像识别

时间为友，记录点滴。

如果上一篇SVM是用来描述What的问题，那么希望这一篇可以稍微深入一点，记录下How的问题。同时，也一起窥探一下机器学习的世界是不是一个稳固的大厦。

SVM的三重境

SVM在机器学习中虽然是用的比较多的，但它绝对不是最简单的那个。但是好在SVM的学习可以是阶梯式的。都说SVM有三宝：间隔、对偶、核技巧。

我们来看SVM的三重境：

• 线性可分情况下的线性分类器

这个是最原始的SVM，它最核心的思想就是最大分类间隔，可以用来解决能够在一个二维（三维）平面上做决策线（面）的例子。（为了统一，我们后面统一用“决策面”来替代，因为线也是面在二维上的投影嘛）

他可以完美的通过“决策面+硬间隔”来分割开待测数据。

来上图看他解决的是哪类问题：

就是我们上一节认识SVM用到的例子

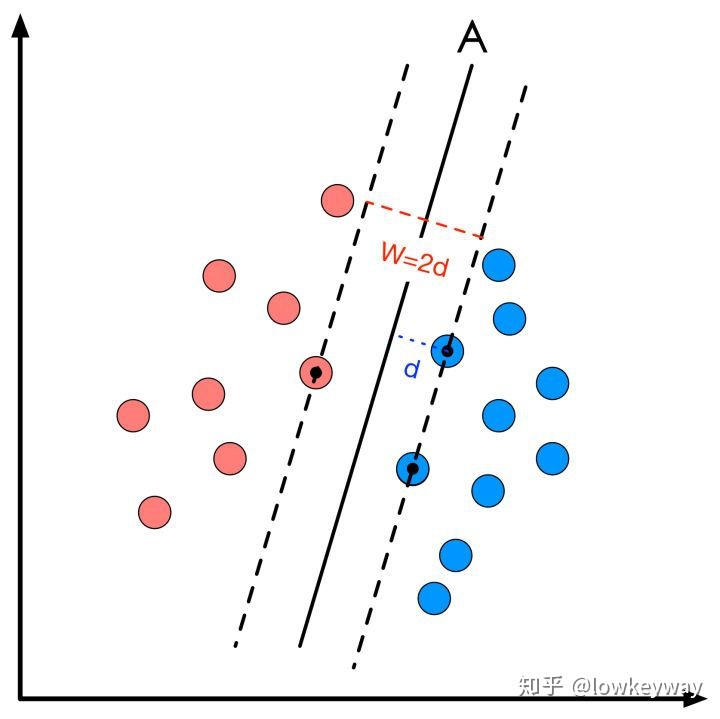
• 线性不可分情况下的线性分类器

完美总是在想象中。在实际开发中，很难找到教科书般的例子让我们寻找决策面来恰好完全区分待测数据，更多的时候，红球、篮球是“你中有我极个别”或“异样点”这种噪声存在的。这个时候，就需要“决策面+软间隔”出马了。

比如下图：

总有一些噪声

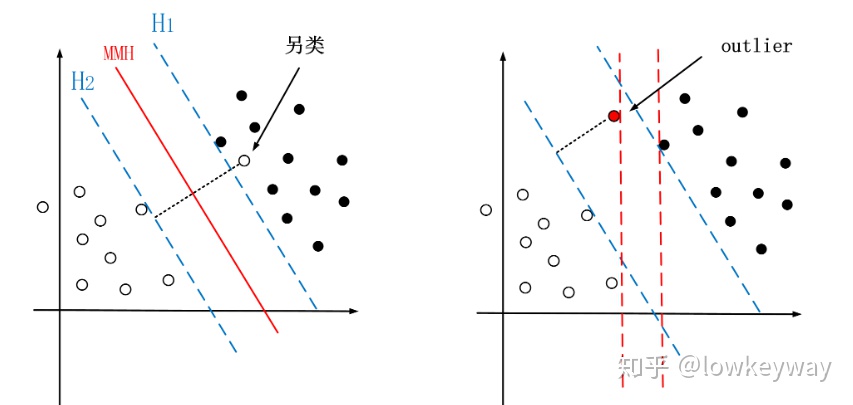
这种情况下虽然是线性不可分，但是我们可以通过引入松弛变量、软误差、惩戒因子等把问题转变成成新的优化问题，而新的优化问题又可以由拉格朗日方程转换成对偶问题。

晕了，晕了！简单理解软间隔就是放宽硬间隔的约束条件（容忍更多错误），从而Pass噪声的过程。

• 线性不可分情况下的非线性分类器

然而，就是有些情况下。上述技术手段都没办法，似乎必须引入非线性分类器了。它是“SVM与核函数（Kernel Function）”的结合。

低维空间的非线性，在高维空间中也许就有明显的决策面。

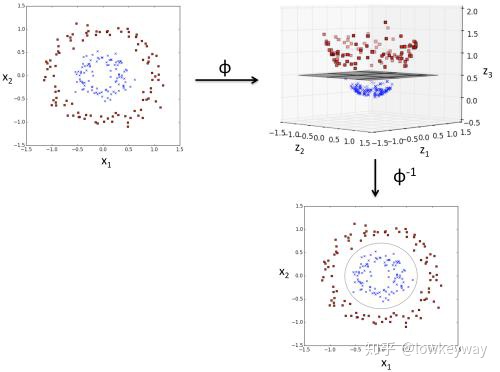
不同的数据落在两个半径不同的圆上，理想的分割界面应该是一个圆圈，而不再是一个决策面了。但是如果把这些数据映射到更高的维度上，分割平面就显而易见了。

而核函数正是用来简化在高维空间中的复杂运算的。

醉了，醉了！简单理解就是就是假如“篮球是氢气球”，“红球是铁球”，那么他们即便混在一起，但是被拉上飞机这么一撒，篮球上升，红球下降，红球和篮球的分割面就自然出现了。

---

1 从分类器到决策面

我觉得对于我们工程师来说，理解SVM的第一重就够了。剩下的就交给算法大神们吧，毕竟要给他们留点饭碗（其实就是因为我数学太差，看不下去后面的公式，呜呜~）。

好，这样，我们讨论SVM就变成了讨论一个线性可分情况下的线性分类器。

1.1 那么，第一个问题是：什么叫线性可分？

线性可分本质上就是指能用线性函数将两类样本完全分开。

那么，我们如何判断数据是不是线性可分的？最简单的情况是数据向量是二维或者三维的，我们可以把图像画出来，直观上就能看出来。

注：对于SVM来说，支持数据必须是线性可分的（当然如果线性不可分我们还有对偶和核技巧两大法宝尝试做到线性可分）

1.2 其次，第二个问题是：什么是线性分类器？

如果线性可分是针对的数据，那么线性分类器就是SVM的核心算法了。

完蛋了，如果有人为了给你解释一个不懂的名词而用了另外一个不懂的名词，那你俩之间肯定有认知差。为了弥补线性分类器这个认知差，我们可以追本溯源从分类器开始说起。

分类器，顾名思义，就是对数据进行划分算法。比如SVM就是一个监督的二分器。但是这里有个问题，数据如此多种多样，怎么做到二分“非黑即白”呢？

实际上，按照NG大神的思路，都是要先铺垫这一部分的。即logistic函数（或称作sigmoid函数）将自变量映射到(0,1)上。

1.2.1 我们先找一个理想状态下的分类函数：

二值图像的阈值

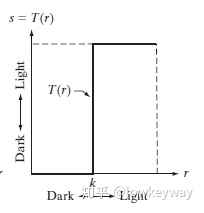
它表示，对于自变量

和对应的分类函数

,在自变量小于

的时候都分类成0这一类，大于等于

的时候则分类成1这一类。可以参考如下公式：

1.2.2 可表示的近似函数-sigmoid函数

我们先看sigmoid函数的几何表示（可以无限接近于理想状态下的分类函数）：

跟阈值函数是否神似？

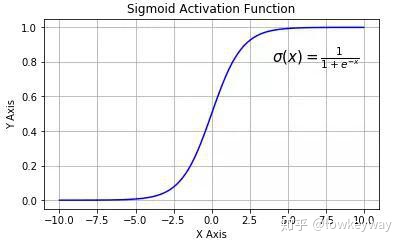
看它的数学表达式：

所以，当我们要判别一个新来的特征属于哪个类时，只需求

即可，如果

大于0.5，就被划到1这一类，反之，就划到0这一类。

1.2.3 寻找SVM的决策面

好了，有了如上做铺垫，相比对分类器有了些许认识。我们再回到SVM中的决策面上来。

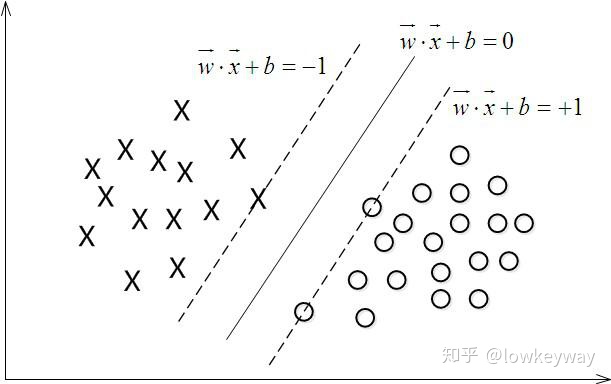
用数学公式表达这个决策面（分类函数）：

（分割超平面）

• 指代超平面法向量，决定了决策面的方向（如果是直线y=kx+b,就好理解了，就是斜率嘛）
• x指代自变量
• b决定了决策面与原点之间的距离（如果是直线，就是截距嘛）
• f(x)指代因变量

所以结合上图：

• 当f(x) 等于0的时候，x便是位于决策面上的点；
• 而f(x)大于0的点对应 y=1 的数据点；
• f(x)小于0的点对应y=-1的点

注：细心的的朋友可能会注意到，sigmoid函数做的分类器都是0和1的两类，而SVM却是-1和1两类，这纯粹是是为了方便之后的运算。毕竟0已经被决策面占了嘛。

很明显，我们这里定义的超平面是一个线性函数，所以它构成的分类器就是线性分类器。

需要注意的是，决策面是有约束条件的（否则它就是空间中无数平凡的超平面中的一个）：

在决策面

确定的情况下，

能够表示点

到距离决策面的远近，而通过观察

的符号与类标记

的

符号是否一致可判断分类是否正确。
即：用

的正负性来判定或表示分类的正确性。

（决策面的约束条件）

---

2 从点面距离到硬间隔

从上一小章中，我们获取了两个信息，必须Mark一下：

• 决策面的表达式：
  ，约束条件为
• 根据
  与0的大小比较分类成1或-1两类

2.1 样本空间到决策面的距离

直接上公式：

其中

为w的二阶范数（范数是一个类似于模的表示长度的概念）

如果我说这是高中的知识你一定不信，但是如果你还记得对于直线方程

，P点坐标

它到直线的距离是

就应该能够差不多理解。

2.2 硬间隔

我们虽然知道了决策面的公式，并且知道了决策面以及数据对应的关系。但是实际上，对于一组线性可分的数据集来说，是由无数多个决策面的。那么SVM的任务就是在无穷个决策面中寻找到最优的那个。

我们认为，这个最优的决策面，应该比其他的决策面有更大的间隔（Margin），而且是硬间隔。正是因为具有这个间隔，最大决策面才是离训练观测最远的分割超平面。

至于如何找到间隔和支持向量，可以回顾一下上一节提到的：
我们沿着 决策线做向两边的平行线，直到碰到两边的第一个有效数据，画两条虚线。
定义两条虚线之间的距离为W为“ 分类间隔”，两边被虚线划中的点叫做“ 支持向量”
那么最佳的决策线应该是所有的支持向量到决策线的垂直距离d 都相等，且最大。

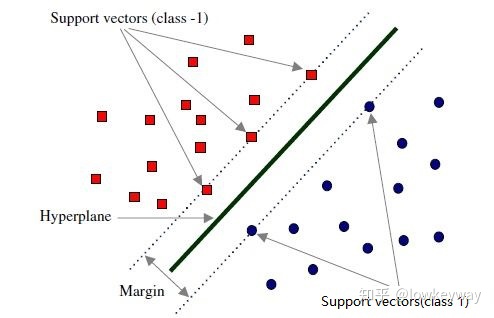
所以，首先应该知道如何表达间隔（用两条平行于决策面的面表示）：

等式两边同除以

，所以它等价于（注意此时的

和

是缩小了

倍的

和

了）：

由决策面的有约束条件，那么间隔也有对应的约束条件：

• 这里的
  的几何意义就是平面在
  轴上的截距。

---

3 SVM拾遗

好了，有了如上作为铺垫，回过头来再想一想，我们的目的是什么？

目的：寻找一个超平面能够最大限度得把两组数据分开！

大象放冰箱的三步走：

第一步、寻找一个超平面

这一步是在空间中任意画一条超平面，难不到我们。1.2.3节已经求过了：

（任意平面）

• 指代超平面法向量，决定了超平面的方向（如果是直线y=kx+b,就好理解了，就是斜率嘛）
• x指代自变量
• b决定了超平面与原点之间的距离（如果是直线，就是截距嘛）
• f(x)指代因变量

第二步、把两组数据分开

这一步就要求这个超平面可以区分开两组数据，构成一个决策面。这个也简单，难不到我们。1.2.3节也提到了，加个约束条件呗（就是只有这些面是符合条件的）

约束条件：

• 当f(x) 等于0的时候，x便是位于超平面上的点；
• 而f(x)大于0的点对应 y=1 的数据点；
• f(x)小于0的点对应y=-1的点

决策面的公式：

约束条件：

即：分类标签

要跟数据

对应的

的符号保持一致。

第三步、最大限度

这一步就要求寻找到的超平面能够最大限度的把两组数据区分开了。

本来，我们应该是寻找

在约束条件下的最大值，但是我们已经知道了决策面（最大超平面）应该是在间隔的中央，并且它由且仅由数据里面的几个

支持向量决定，那么我们就可以把这个问题转变成求解支持向量（点）到决策面（面）的最大值求解的问题：

已知，支持向量上的点到面的距离为：

而支持向量

对应的

在约束条件下不就等于1吗？即：

那么求

的最大值问题，就可以等价成求

的最小值问题。

当然，别忘了约束条件为：

完美！饶了大半天，求解最优决策面的问题，转换成公式就是定格

中

和

的过程，而推导半天，也恰恰是求解

的过程。

至于如何求解

的最小值，可以等价于求

的最小值，它是一个典型的不等式约束条件下的二次型函数优化问题，就不展开说了（其实是因为后面拉格朗日、KTT我也看不动。。）

---

通过以上步骤，至少应该对SVM的决策线的确立，以及为什么要支持向量有了更理性的认识。作为一名工程师，不能只加深概念理解，我们试试SVM除了Demo还能干点什么具体的事情！

C++

注意事项：

1. 本文中采用的素材来自OpenCV的源码中目录opencv-4.1.1samplesdatadigits.png文件；
2. 下面的代码对OpenCV的版本号以及VS 是64位敏感；比如__int64、_findfirst64、_findnext64接口需要64位机，；SVM的定义Ptr<ml::SVM> svm;以及其关键参数的设定都跟老版本不同（我使用的是OpenCV 4.1.1 + VS64）
3. 代码虽然看起来很长，但是分模块只有三个部分：图像分割；SVM训练；目标图片识别；
4. 因为并不是每次都需要依次做图像分割、SVM训练和目标图片识别，所以我增加了NEED_SPLIT、NEED_TRAIN、NEED_PREDICT三个宏，可以根据需要打开对应的宏定义。

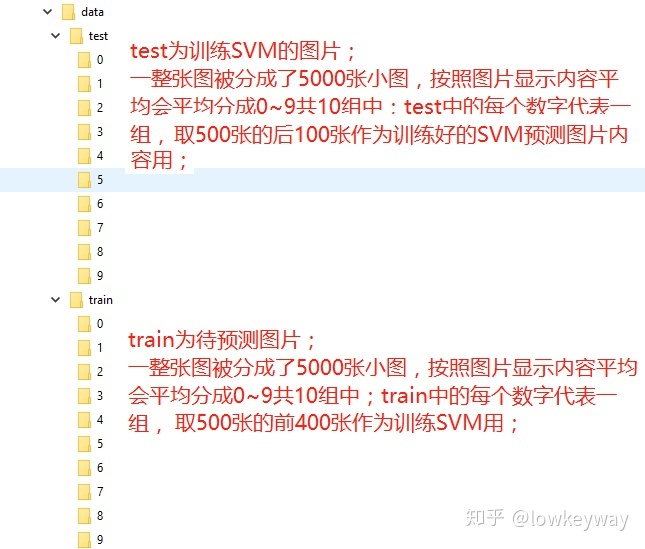
• 图像分割--splitPic

1. digist原图大小为2000x1000， 我们把它分割成50000个20x20的小图；
2. 其中，按照图片内容，分成0~9共10组，每组是500张内容相近的图片（比如都是0）
3. train目录下的0~9，每个目录放一组的前400张图片用来训练SVM，同理，test目录下的0~9，每个目录放一组的后100张图片用来做图片内容预测；

• SVM训练--svmTrain

1. 首先，先给train中的所有内容打上标签（其实就是图片对应的文件夹的名字0~9）；
2. 定义SVM并且设置相关参数；
3. 调用train，训练即可；
4. 最后用save保存训练好的SVM为xml文件；

• 目标图片识别 --svmPredict

1. 首先加载训练过的xml文件，还原SVM；
2. 直接把待预测的图片丢进predict函数即可得到预测值；
3. 可以看看预测值跟期望值是否一致；

#include 

运行结果；速度比较慢，耐心等待奥。

digits.png

我把代码也素材上传到了github，参考一起学习。

https://github.com/lowkeyway/OpenCV/tree/master/section43%23SVM-Math/C%2B%2B